10 câu hỏi trắc nghiệm thuộc Dạng 1: Tìm tổng của hai hay nhiều vectơ có đáp án

Câu 1:

Cho O là trung điểm của AB. Ta có: $\vec{A B} + \vec{O A} = ?$

A. $\vec{A B}$

B.

\vec{O A}

;

C.

\vec{B O}

;

D.

\vec{O B}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, O, B ta có:

$\vec{A B} + \vec{O A} = \vec{O A} + \vec{A B} = \vec{O B}$ .

Câu 2:

Cho 4 điểm A, B, C, D. Ta có: $\vec{A B} + \vec{B D} = ?$

A.

\vec{A C} + \vec{B D}

;

B.

\vec{A D} + \vec{D B}

;

C.

\vec{A C} + \vec{C D}

;

D.

\vec{D A} + \vec{D B}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Áp dụng quy tắc ba điểm cho ba điểm A, D, B ta có: $\vec{A B} + \vec{B D} = \vec{A D}$ .

Áp dụng quy tắc ba điểm cho ba điểm A, D, C ta có: $\vec{A C} + \vec{C D} = \vec{A D}$ .

Vậy $\vec{A B} + \vec{B D} = \vec{A C} + \vec{C D}$ .

Câu 3:

Cho các điểm A, B, C phân biệt. Đẳng thức nào sau đây đúng ?

A.

\vec{A B} = \vec{B C} + \vec{C A}

;

B.

\vec{A B} = \vec{C B} + \vec{A C}

;

C.

\vec{A B} = \vec{B C} + \vec{A C}

;

D.

\vec{A B} = \vec{C A} + \vec{B C}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, C, B ta có: $\vec{C B} + \vec{A C} = \vec{A C} + \vec{C B} = \vec{A B}$

Vậy $\vec{A B} = \vec{C B} + \vec{A C}$ .

Câu 4:

Cho hình bình hành ABCD tâm O. Khi đó, $\vec{O A} + \vec{B O} = ?$

A.

\vec{O C} + \vec{O B}

;

B.

\vec{A B}

;

C.

\vec{O C} + \vec{D O}

;

D.

\vec{C D}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

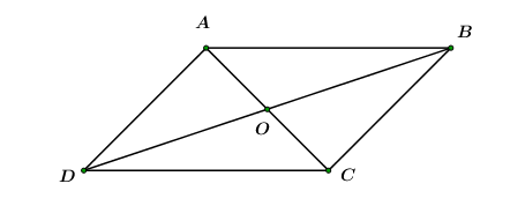
Cho hình bình hành ABCD tâm O. Khi đó, vecto OA+ vecto BO=? (ảnh 1)

Áp dụng tính chất giao hoán và quy tắc ba điểm cho ba điểm A, O, B ta có: $\vec{O A} + \vec{B O} = \vec{B O} + \vec{O A} = \vec{B A}$ .

Xét hình bình hành ABCD có: $\vec{B A} = \vec{C D}$

Vậy $\vec{O A} + \vec{B O} = \vec{C D}$

Câu 5:

Cho hình vuông ABCD tâm O. Khi đó: $\vec{A B} + \vec{A D} = ?$

A.

\vec{A B}

;

B.

\vec{B C}

;

C.

\vec{B D}

;

D.

\vec{A C}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

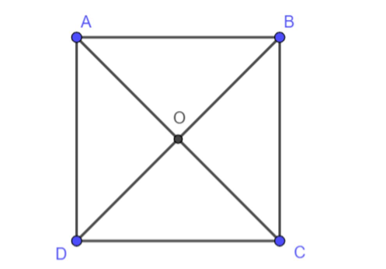
Cho hình vuông ABCD tâm O. Khi đó: vecto AB+ AD=? (ảnh 1)

Áp dụng quy tắc hình bình hành cho hình vuông ABCD có: $\vec{A B} + \vec{A D} = \vec{A C}$ .

Câu 6:

Cho 6 điểm A, B, C, D, E, F. Đẳng thức nào sau đây đúng.

A. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C} + \vec{E F} + \vec{D E} = \vec{0}$

B. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C} + \vec{E F} + \vec{D E} = \vec{A E}$

C. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C} + \vec{E F} + \vec{D E} = \vec{A F}$

D. $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C} + \vec{E F} + \vec{D E} = \vec{A D}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Ta có:

$\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C} + \vec{E F} + \vec{D E}$

$= (\vec{A B} + \vec{B C}) + (\vec{C D} + \vec{D E}) + (\vec{E F} + \vec{F A})$

$= \vec{A C} + \vec{C E} + \vec{E A}$

$= (\vec{A C} + \vec{C E}) + \vec{E A}$

$= \vec{A E} + \vec{E A}$

$= \vec{A A} = \vec{0}$

Vậy $\vec{A B} + \vec{C D} + \vec{F A} + \vec{B C} + \vec{E F} + \vec{D E} = \vec{0}$ .

Câu 7:

Cho các điểm M, N, P, Q, R. Tính $\vec{M N} + \vec{P Q} + \vec{R N} + \vec{N P} + \vec{Q R}$ = ?

A. $\vec{M R}$

B. $\vec{M Q}$

C. $\vec{M P}$

D. $\vec{M N}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

$\vec{M N} + \vec{P Q} + \vec{R N} + \vec{N P} + \vec{Q R}$

$= (\vec{M N} + \vec{N P}) + (\vec{P Q} + \vec{Q R}) + \vec{R N}$

$= \vec{M P} + \vec{P R} + \vec{R N}$

$= (\vec{M P} + \vec{P R}) + \vec{R N}$

$= \vec{M R} + \vec{R N} = \vec{M N}$

Vậy $\vec{M N} + \vec{P Q} + \vec{R N} + \vec{N P} + \vec{Q R} = \vec{M N}$ .

Câu 8:

Cho hình bình hành ABCD tâm O. Khẳng định nào sau đây là đúng ?

A. $\vec{A O} + \vec{B O} = \vec{B D}$

B. $\vec{A O} + \vec{A C} = \vec{B O}$

C. $\vec{O B} + \vec{A O} = \vec{C D}$

D. $\vec{A B} + \vec{C A} = \vec{D A}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

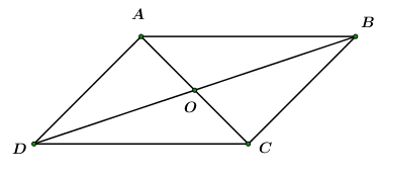
Cho hình bình hành ABCD tâm O. Khẳng định nào sau đây là đúng ? (ảnh 1)

Ta có: $\vec{A B} = \vec{D C}$ (do ABCD là hình bình hành)

Do đó: $\vec{A B} + \vec{C A} = \vec{D C} + \vec{C A} = \vec{D A}$

Câu 9:

Cho 4 điểm A, B, C, D. Ta có: $\vec{A B} + \vec{C D} + \vec{D A} + \vec{B C} = ?$

A. $\vec{D B}$

B. $\vec{B D}$

C. $\vec{0}$

D. $\vec{D A}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có:

$\vec{A B} + \vec{C D} + \vec{D A} + \vec{B C}$

$= (\vec{A B} + \vec{B C}) + (\vec{C D} + \vec{D A})$

$= \vec{A C} + \vec{C A} = \vec{A A} = \vec{0}$

Vậy $\vec{A B} + \vec{C D} + \vec{D A} + \vec{B C} = \vec{0}$ .

Câu 10:

Cho hình bình hành ABCD, M, N lần lượt là trung điểm của AD và BC. Khi đó, $\vec{A D} + \vec{M B} + \vec{N A} = ?$

A. $\vec{D B}$

B. $\vec{M N}$

C. $\vec{0}$

D. $\vec{D A}$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

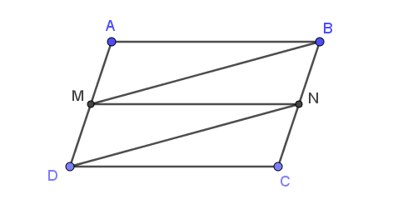
Cho hình bình hành ABCD, M, N lần lượt là trung điểm của AD và BC. Khi đó, (ảnh 1)

Do ABCD là hình bình hành nên AD // BC, AD = BC.

M, N lần lượt là trung điểm của AD và BC nên ta suy ra được:

AB = MN = DC, AM = MD = BN = NC, MN // AB // DC

Xét tam giác AMB và tam giác MDN có:

AM = MD

AB = MN

$\hat{M A B} = \hat{D M N}$ (hai góc đồng vị do MN // AB )

Do đó, tam giác AMB và tam giác MDN bằng nhau

⇒ MB = DN (1) và $\hat{A M B} = \hat{M D N}$ (2)

Từ (2) ta suy ra MB // DN (3)

Từ (1) và (3) ta suy ra: $\vec{M B} = \vec{D N}$

Ta có: $\vec{A D} + \vec{M B} + \vec{N A} = \vec{A D} + (\vec{D N} + \vec{N A}) = \vec{A D} + \vec{D A} = \vec{A A} = \vec{0}$ .

Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án

Dạng 1: Tìm tổng của hai hay nhiều vectơ có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương