10 câu hỏi trắc nghiệm thuộc Dạng 5: Xác định các điểm thỏa mãn đẳng thức vectơ có đáp án

Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án

Dạng 5: Xác định các điểm thỏa mãn đẳng thức vectơ có đáp án

651 lượt thi
10 câu hỏi
0 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Cho tam giác ABC có M thỏa mãn điều kiện $\vec{M A} + \vec{M B} + \vec{M C} = \vec{0}$ . Vị trí điểm M là:

A. M là điểm thứ tư của hình bình hành ACBM;

B. M là trung điểm của đoạn thẳng AB;

C. M trùng C;

D. M là trọng tâm tam giác ABC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Gọi G là trọng tâm tam giác ABC ta có: $\vec{G A} + \vec{G B} + \vec{G C} = \vec{0}$

Do đó: $\vec{M A} + \vec{M B} + \vec{M C} = \vec{G A} + \vec{G B} + \vec{G C}$

Nên M trùng với G hay M là trọng tâm tam giác ABC.

Câu 2:

Cho tam giác ABC. Tập hợp các điểm M thỏa mãn $|\vec{M B} - \vec{M C}| = |\vec{B M} - \vec{B A}|$ là:

A. đường thẳng AB;

B. trung trực đoạn BC;

C. đường tròn tâm A bán kính BC;

D. đường thẳng qua A và song song với BC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có:

$|\vec{M B} - \vec{M C}| = |\vec{B M} - \vec{B A}| \Leftrightarrow |\vec{C B}| = |\vec{A M}|$ ⇔ CB = AM.

Mà A, B, C cố định nên M là điểm thuộc đường tròn tâm A bán kính BC.

Câu 3:

Cho tam giác ABD. Xác định điểm C sao cho: $\vec{A B} + \vec{A D} = \vec{A C}$ .

A. C là một đỉnh của hình bình hành ABCD;

B. C là trọng tâm tam giác ABD;

C. C là trung điểm AB;

D. C là trung điểm BD.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

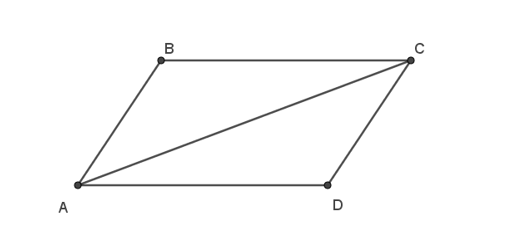
Theo quy tắc hình bình hành ta có: $\vec{A B} + \vec{A D} = \vec{A C}$ .

Vậy C là một đỉnh của hình bình hành ABCD.

Cho tam giác ABD. Xác định điểm C sao cho: vecto AB+ vecto AD= vecto AC (ảnh 1)

Câu 4:

Cho 2 điểm A, B với A cố định. Xác định điểm B sao cho: $|\vec{A B}| = 4$ .

A. B là điểm thuộc đường tròn tâm A bán kính 2;

B. B là điểm thuộc đường tròn tâm A bán kính 4;

C. B là điểm thuộc đường tròn đi qua A bán kính 4;

D. B là điểm thuộc đường tròn đi qua A bán kính 2.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có: $|\vec{A B}| = 4$ ⇔ AB = 4.

Vì A cố định.

Do đó, B là điểm thuộc đường tròn tâm A bán kính 4.

Câu 5:

Cho 3 điểm A, B, M với B cố định. Xác định điểm A sao cho: $|M A - M B| = 5$ .

A. A là điểm thuộc đường tròn tâm M bán kính 5;

B. A là điểm thuộc đường tròn tâm B bán kính 5;

C. A là điểm thuộc đường tròn đi qua M bán kính 25;

D. A là điểm thuộc đường tròn đi qua B bán kính 25.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có:

$|M A - M B| = 5 \Leftrightarrow |\vec{B A}| = 5 \Leftrightarrow B A = 5$

Vì B cố định

Vậy A là điểm thuộc đường tròn tâm B bán kính 5.

Câu 6:

Cho đoạn thẳng AB, biết $|\vec{I A}| = |\vec{I B}|$ . Xác định tập hợp điểm I.

A. Tập hợp điểm I là đường thẳng AB;

B. Tập hợp điểm I là đường tròn đường kính AB;

C. Tập hợp điểm I là đường trung trực của đoạn thẳng AB;

D. Tập hợp điểm I là đường tròn bán kính AB.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có: $|\vec{I A}| = |\vec{I B}|$ ⇔ IA = IB.

Do đó, I thuộc đường trung trực của đoạn thẳng AB.

Câu 7:

Cho hình bình hành ABCD và điểm M, biết $|\vec{B M} - \vec{B A}| = |\vec{A B} + \vec{A D}|$ . Điểm M là:

A. Điểm thuộc đường tròn tâm A bán kính AC;

B. Điểm thuộc đường tròn tâm A bán kính BD;

C. Điểm thuộc đường tròn tâm B bán kính AC;

D. Điểm thuộc đường tròn tâm B bán kính BD.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Cho hình bình hành ABCD và điểm M, biết | vecto BM-BA| = | vecto AB+AD|. Điểm M là: (ảnh 1)

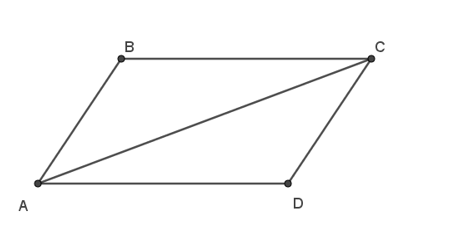
Xét hình bình hành ABCD có: $\vec{A B} + \vec{A D} = \vec{A C}$ .

Ta có: $|\vec{B M} - \vec{B A}| = |\vec{A B} + \vec{A D}| \Leftrightarrow |\vec{A M}| = |\vec{A C}|$ .

Do A, C cố định nên $|\vec{A C}|$ cố định là một số thực.

Vậy M là điểm thuộc đường tròn tâm A bán kính AC.

Câu 8:

Cho đoạn thẳng CD, biết $|\vec{M C}| = |\vec{D M}|$ . Điểm M:

A. thuộc đường thẳng CD;

B. thuộc đường trung trực của đoạn thẳng CD;

C. thuộc đường tròn đường kính CD;

D. thuộc đường tròn bán kính CD.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có: $|\vec{M C}| = |\vec{D M}| \Leftrightarrow |\vec{M C}| = |\vec{M D}|$ ⇔ MC = MD.

Do đó, M thuộc đường trung trực của đoạn thẳng CD.

Câu 9:

Cho hình thoi ABCD tâm O và điểm I, biết $|\vec{B O} - \vec{M O}| = |\vec{O D} + \vec{O C}|$ . Điểm I là:

A. Điểm thuộc đường tròn tâm O bán kính AC;

B. Điểm thuộc đường tròn tâm O bán kính BD;

C. Điểm thuộc đường tròn tâm B bán kính BC;

D. Điểm thuộc đường tròn tâm B bán kính AC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Cho hình thoi ABCD tâm O và điểm I, biết | vecto BO-MO| = | vecto OD-OC|. Điểm I là: (ảnh 1)

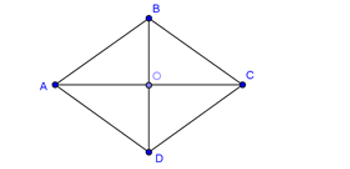
Hình thoi ABCD tâm O nên O là trung điểm của AC và BD, do đó ta có: $\vec{O D} = \vec{B O}$ .

Lại có: $|\vec{B O} - \vec{M O}| = |\vec{O D} + \vec{O C}|$

$\Leftrightarrow |\vec{B O} + \vec{O M}| = |\vec{B O} + \vec{O C}|$

$\Leftrightarrow |\vec{B M}| = |\vec{B C}|$ .

Vì B, C cố định nên M là điểm thuộc đường tròn tâm B bán kính BC.

Câu 10:

Cho tam giác ABC và điểm K thỏa mãn $\vec{A K} + \vec{B K} + \vec{C K} = \vec{0}$ . Xác định điểm K ?

A. K là điểm thứ tư của hình bình hành ACBK;

B. K là trung điểm của đoạn thẳng AB;

C. K trùng C;

D. K là trọng tâm tam giác ABC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Ta có:

$\vec{A K} + \vec{B K} + \vec{C K} = \vec{0}$

$\Leftrightarrow - \vec{A K} - \vec{B K} - \vec{C K} = \vec{0}$

$\Leftrightarrow \vec{K A} + \vec{K B} + \vec{K C} = \vec{0}$

Vậy K là trọng tâm của tam giác ABC.

Bắt đầu thi ngay

Trắc nghiệm Toán 10 CTST Bài 2: Tìm tổng của hai hay nhiều vectơ có đáp án

Dạng 5: Xác định các điểm thỏa mãn đẳng thức vectơ có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương