Dạng 1: Hàm số và đồ thị Cách xác định một hàm số, cách cho một hàm số có đáp án
-
443 lượt thi
-
14 câu hỏi
-
0 phút
Danh sách câu hỏi
Câu 1:
Cho bảng giá trị x, y như sau:
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
34 |
41 |
13 |
34 |
93 |
Đại lượng y có phải là hàm số của đại lượng x không ?
Xem đáp án
Hướng dẫn giải:
Ta có, x, y là hai đại lượng biến thiên và x nhận giá trị thuộc tập số:
D = {1; 2; 3; 4; 5}
Với mỗi giá trị x thuộc D, theo bảng trên, ta xác định được một và chỉ một giá trị y tương ứng thuộc tập số thực. Do đó, đại lượng y là hàm số của đại lượng x.
Câu 2:
Xem đáp án
Hướng dẫn giải:
Ta có, x, y là hai đại lượng biến thiên và y nhận giá trị thuộc tập số:
D = {34; 41; 13; 93}
Với giá trị y = 34, theo bảng trên, ta xác định được hai giá trị x tương ứng là x = 1 và x = 4, do đó, đại lượng x không là hàm số của y.
Câu 3:
Thực hiện các yêu cầu sau:
Cho biểu đồ sau:
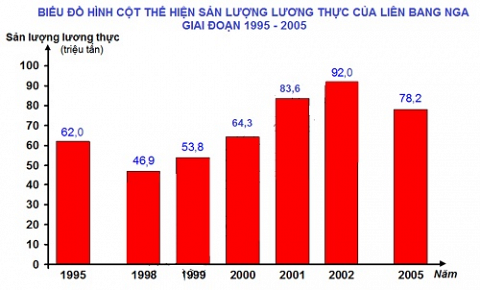
Biểu đồ này có biểu thị một hàm số không ? Tại sao ?
Xem đáp án
Hướng dẫn giải:
Gọi x là giá trị năm, y là giá trị sản lượng lương thực.
Ta dễ thấy, x và y là hai đại lượng biến thiên. Trong đó, x nhận giá trị thuộc tập số:
D = {1995; 1998; 1999; 2000; 2001; 2002; 2005}
Với mỗi giá trị x thuộc D, theo bảng trên, ta xác định được một và chỉ một giá trị y tương ứng thuộc tập số thực. Do đó, đại lượng y là hàm số của đại lượng x.
Vậy biểu đồ trên biểu thị một hàm số y = f(x).
Câu 4:
Xem đáp án
Hướng dẫn giải:
Xét hàm số y = f(x) = 3x
Ta có: Tại giá trị x = 4 thì y = f(4) = 3.4 = 12
Vậy giá trị y = 12 tương ứng với giá trị x = 4.
Câu 5:
Cho bảng sau:
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
+ Xét bảng trên ta thấy x và y là hai đại lượng biến thiến, giá trị của x thuộc tập số:
D =\(\left\{ {1;2;3;0;\frac{{ - 3}}{2}; - 2; - 4} \right\}\)
Với mỗi giá trị của x chỉ có một giá trị duy nhất của y. Vậy y là hàm số của x.
+ Đại lượng x không là hàm số của y vì với giá trị y = 2, cho ta 2 giá trị của x là x = 1 và \(x = - \frac{3}{2}\).
Câu 6:
Cho hàm số: y = 3x – 5. Hãy cho biết giá trị của y khi x = 3.
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Xét hàm số: y = 3x – 5. Khi x = 3 ta có: y = 3.3 – 5 = 9 – 5 = 4
Vậy khi x = 3 thì giá trị y tương ứng là 4.
Câu 7:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Xét hàm số y = f(x) = 3x3 – 1.
Ta có: f(2) = 3.23 – 1 = 24 – 1 = 23.
Câu 8:
Cho bảng sau:
Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Xét bảng trên, dễ thấy:
Ứng với giá trị x = –5 là y = –10
Ứng với giá trị x = 1 là y = 8
Ứng với giá trị x = 3 là y = 14
Ứng với giá trị x = 8 là y = 29.
Câu 9:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A.
Xét hàm số y = f(x) = 9x2 – 17. Ta có:
f(3) = 9.32 – 17 = 81 – 17 = 64.
Câu 10:
Cho biểu đồ sản lượng theo năm như sau:
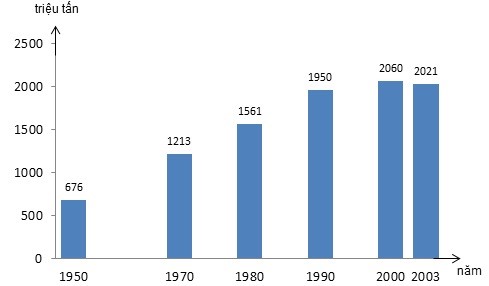
Gọi sản lượng là y, giá trị năm là x. Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Xét biểu đồ ta thấy:
x, y là hai đại lượng biến thiên. Trong đó, x nhận giá trị thuộc tập số:
D = {1950; 1970; 1980; 1990; 2000; 2003}.
Với mỗi giá trị của x chỉ có một giá trị duy nhất của y. Vậy y là hàm số của x.
Vậy biểu đồ trên biểu thị một hàm số.
Từ biểu đồ, ta thấy:
Tại x = 1990 thì y = 1950.
Tại x = 2000 thì y = 2060.
Câu 11:
Cho biểu đồ:
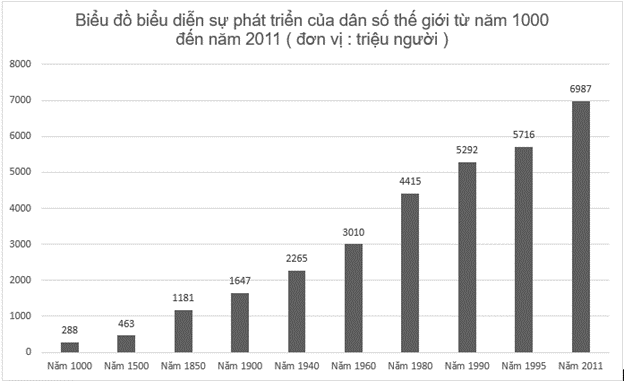
Gọi x là giá trị năm, y là dân số (triệu người). Biểu đồ biểu thị hàm số y = f(x). Khẳng định nào sau đây là đúng ?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Dựa vào biểu đồ ta thấy:
f(1940) = 2265
f(2011) = 6987
f(1500) = 463
f(1000) = 288
Do đó, f(1000) < f(1500).
Câu 12:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: f(2) = 23 – 22 = 4, f(1) = 13 – 12 = 0, f(0) = 0.
Do đó, f(2) > f(1), f(1) = f(0).
Lại có: f(3) = 33 – 32 = 18, f(4) = 43 – 42 = 48
Do đó f(4) > f(3), f(4) > 0.
Câu 13:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B.
Ta có: f(1) = 3.14 = 3; f(0) = 3.04 = 0
Mà: 3 – 0 = 3
Do đó, f(1) – f(0) = f(1).
Ta có: f(2) = 3.24 = 48, f(4) = 3.44 = 768, f(5) = 3.54 = 1875.
Vậy f(2) – f(1) = 48 – 3 = 45 và f(4) ≠ f(5).
Câu 14:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C.
Ta có:
f(1) = 2.13 – 4 = –2 < 0
f(3) = 2.33 – 4 = 50
Ta có:
f(1) – f(3) = –2 – 50 = –52
f(1) + f(3) = –2 + 50 = 48