Câu hỏi:
03/04/2024 37
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?
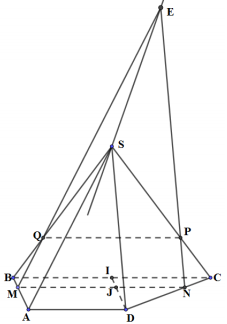
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?

Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
+) \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \subset \left( P \right)\\a//\left( Q \right)\end{array} \right. \Rightarrow a//d\)
+) \(\left\{ \begin{array}{l}a,b \subset \left( P \right)\\a',\,b' \subset \left( Q \right)\\a//a',\,b//b'\\a \cap b = \left\{ I \right\}\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\)
+) \(\left\{ \begin{array}{l}\left( P \right)//\left( Q \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow a//\left( Q \right)\)
Cách giải:
a) Ta có: \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SAB} \right) = MQ\\SA \subset \left( {SA{\rm{D}}} \right)\\SA//\left( {MNPQ} \right)\end{array} \right. \Rightarrow MQ//SA\) (1)
Do \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SBC} \right) = PQ\\BC \subset \left( {SBC} \right)\\BC//\left( {MNPQ} \right)\end{array} \right. \Rightarrow BC//PQ\). Mà \(A{\rm{D//BC}} \Rightarrow {\rm{PQ//AD}}\) (2)
Từ (1), (2) suy ra: \(\left( {MNPQ} \right)//\left( {SA{\rm{D}}} \right) \Rightarrow NP//\left( {SA{\rm{D}}} \right)\) (do \(NP \subset \left( {MNPQ} \right)\))
b) Ta có: \[E = MQ \cap NP\].
Mà \[MQ \subset \left( {SAB} \right),NP \subset \left( {SC{\rm{D}}} \right) \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\]
\[ \Rightarrow \] E luôn di động trên một đường thẳng cố định, chính là giao tuyến của (SAB) và (SCD).
c) Thiết diện của hình chóp cắt bởi \[\left( \alpha \right)\] là hình thang MNPQ (do \[MN//PQ\left( {//BC} \right)\])
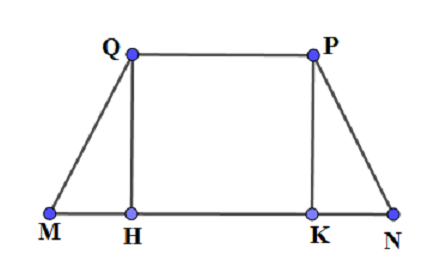
Ta có: \[\left\{ \begin{array}{l}MQ//SA\\MN//A{\rm{D}}\end{array} \right. \Rightarrow MQN = SA{\rm{D}} = 60^\circ \] (do tam giác SAD đều)
\[\left\{ \begin{array}{l}NP//S{\rm{D}}\\MN//A{\rm{D}}\end{array} \right. \Rightarrow QPN = S{\rm{D}}A = 60^\circ \] (do tam giác SAD đều)
\[ \Rightarrow MQN = QPN \Rightarrow \]MNPQ là hình thang cân.
+) \[MQ//SA \Rightarrow \frac{{AM}}{{AB}} = \frac{{MQ}}{{SA}} = \frac{{SQ}}{{SB}} = \frac{x}{a} \Rightarrow \left\{ \begin{array}{l}MQ = \frac{x}{a}.SA = \frac{x}{a}.a = x\\\frac{{SQ}}{{SB}} = \frac{x}{a}\end{array} \right.\]
+) \[PQ//BC \Rightarrow \frac{{PQ}}{{BC}} = \frac{{SQ}}{{SB}} = \frac{x}{a} \Rightarrow PQ = \frac{x}{a}.BC = \frac{x}{a}.2{\rm{a}} = 2{\rm{x}}\]
+) Gọi I là trung điểm của BC, J là giao điểm của ID và MN
Khi đó, ABID là hình thoi có các cạnh đều bằng a \[ \Rightarrow {\rm{MJ = a}}\] (do \[MJ//BI//A{\rm{D}}\])
\[JN//IC \Rightarrow \frac{{JN}}{{IC}} = \frac{{J{\rm{D}}}}{{I{\rm{D}}}} = \frac{{AM}}{{AB}} = \frac{x}{a} \Rightarrow JN = \frac{x}{a}.IC = \frac{x}{a}.a = x \Rightarrow MN = a + x\]
Gọi H, K lần lượt là hình chiếu của Q, P lên MN.
Do MNPQ là hình thang cân nên
\[MH = KN = \frac{{MN - PQ}}{2} = \frac{{x + a - 2{\rm{x}}}}{2} = \frac{{a - x}}{2}\]
\[\Delta MQH\] vuông tại H \[ \Rightarrow QH = MH.\tan 60^\circ = \frac{{a - x}}{2}.\sqrt 3 \]
Diện tích hình thang MNPQ là:
\[{S_{MNPQ}} = \frac{1}{2}\left( {PQ + MN} \right).QH = \frac{1}{2}.\left( {2{\rm{x}} + x + a} \right).\frac{{\sqrt 3 }}{2}\left( {a - x} \right)\]
\[ = \frac{{\sqrt 3 }}{{12}}\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right)\]
Áp dụng BĐT Cô si, ta có: \[\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right) \le {\left( {\frac{{3{\rm{x}} + a + 3{\rm{a}} - 3{\rm{x}}}}{2}} \right)^2} = 4{{\rm{a}}^2}\]
\[ \Rightarrow \frac{{\sqrt 3 }}{{12}}\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right) \le \frac{{\sqrt 3 }}{{12}}.4{{\rm{a}}^2} = \frac{{{a^2}\sqrt 3 }}{3} \Rightarrow {S_{MNPQ}} \le \frac{{{a^2}\sqrt 3 }}{3}\]
Dấu “=” xảy ra khi và chỉ khi \[3{\rm{x}} + a = 3{\rm{a}} - 3{\rm{x}} \Leftrightarrow x = \frac{2}{3}a\]
Vậy, diện tích thiết diện MNPQ đạt giá trị lớn nhất \[\frac{{{a^2}\sqrt 3 }}{3}\] khi và chỉ khi M nằm trên cạnh AB sao cho \[AM = \frac{2}{3}a\].
Phương pháp:
+) \(\left\{ \begin{array}{l}\left( P \right) \cap \left( Q \right) = d\\a \subset \left( P \right)\\a//\left( Q \right)\end{array} \right. \Rightarrow a//d\)
+) \(\left\{ \begin{array}{l}a,b \subset \left( P \right)\\a',\,b' \subset \left( Q \right)\\a//a',\,b//b'\\a \cap b = \left\{ I \right\}\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\)
+) \(\left\{ \begin{array}{l}\left( P \right)//\left( Q \right)\\a \subset \left( P \right)\end{array} \right. \Rightarrow a//\left( Q \right)\)
Cách giải:
a) Ta có: \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SAB} \right) = MQ\\SA \subset \left( {SA{\rm{D}}} \right)\\SA//\left( {MNPQ} \right)\end{array} \right. \Rightarrow MQ//SA\) (1)
Do \(\left\{ \begin{array}{l}\left( {MNPQ} \right) \cap \left( {SBC} \right) = PQ\\BC \subset \left( {SBC} \right)\\BC//\left( {MNPQ} \right)\end{array} \right. \Rightarrow BC//PQ\). Mà \(A{\rm{D//BC}} \Rightarrow {\rm{PQ//AD}}\) (2)
Từ (1), (2) suy ra: \(\left( {MNPQ} \right)//\left( {SA{\rm{D}}} \right) \Rightarrow NP//\left( {SA{\rm{D}}} \right)\) (do \(NP \subset \left( {MNPQ} \right)\))
b) Ta có: \[E = MQ \cap NP\].
Mà \[MQ \subset \left( {SAB} \right),NP \subset \left( {SC{\rm{D}}} \right) \Rightarrow E \in \left( {SAB} \right) \cap \left( {SC{\rm{D}}} \right)\]
\[ \Rightarrow \] E luôn di động trên một đường thẳng cố định, chính là giao tuyến của (SAB) và (SCD).
c) Thiết diện của hình chóp cắt bởi \[\left( \alpha \right)\] là hình thang MNPQ (do \[MN//PQ\left( {//BC} \right)\])

Ta có: \[\left\{ \begin{array}{l}MQ//SA\\MN//A{\rm{D}}\end{array} \right. \Rightarrow MQN = SA{\rm{D}} = 60^\circ \] (do tam giác SAD đều)
\[\left\{ \begin{array}{l}NP//S{\rm{D}}\\MN//A{\rm{D}}\end{array} \right. \Rightarrow QPN = S{\rm{D}}A = 60^\circ \] (do tam giác SAD đều)
\[ \Rightarrow MQN = QPN \Rightarrow \]MNPQ là hình thang cân.
+) \[MQ//SA \Rightarrow \frac{{AM}}{{AB}} = \frac{{MQ}}{{SA}} = \frac{{SQ}}{{SB}} = \frac{x}{a} \Rightarrow \left\{ \begin{array}{l}MQ = \frac{x}{a}.SA = \frac{x}{a}.a = x\\\frac{{SQ}}{{SB}} = \frac{x}{a}\end{array} \right.\]
+) \[PQ//BC \Rightarrow \frac{{PQ}}{{BC}} = \frac{{SQ}}{{SB}} = \frac{x}{a} \Rightarrow PQ = \frac{x}{a}.BC = \frac{x}{a}.2{\rm{a}} = 2{\rm{x}}\]
+) Gọi I là trung điểm của BC, J là giao điểm của ID và MN
Khi đó, ABID là hình thoi có các cạnh đều bằng a \[ \Rightarrow {\rm{MJ = a}}\] (do \[MJ//BI//A{\rm{D}}\])
\[JN//IC \Rightarrow \frac{{JN}}{{IC}} = \frac{{J{\rm{D}}}}{{I{\rm{D}}}} = \frac{{AM}}{{AB}} = \frac{x}{a} \Rightarrow JN = \frac{x}{a}.IC = \frac{x}{a}.a = x \Rightarrow MN = a + x\]
Gọi H, K lần lượt là hình chiếu của Q, P lên MN.
Do MNPQ là hình thang cân nên
\[MH = KN = \frac{{MN - PQ}}{2} = \frac{{x + a - 2{\rm{x}}}}{2} = \frac{{a - x}}{2}\]
\[\Delta MQH\] vuông tại H \[ \Rightarrow QH = MH.\tan 60^\circ = \frac{{a - x}}{2}.\sqrt 3 \]
Diện tích hình thang MNPQ là:
\[{S_{MNPQ}} = \frac{1}{2}\left( {PQ + MN} \right).QH = \frac{1}{2}.\left( {2{\rm{x}} + x + a} \right).\frac{{\sqrt 3 }}{2}\left( {a - x} \right)\]
\[ = \frac{{\sqrt 3 }}{{12}}\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right)\]
Áp dụng BĐT Cô si, ta có: \[\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right) \le {\left( {\frac{{3{\rm{x}} + a + 3{\rm{a}} - 3{\rm{x}}}}{2}} \right)^2} = 4{{\rm{a}}^2}\]
\[ \Rightarrow \frac{{\sqrt 3 }}{{12}}\left( {3{\rm{x}} + a} \right)\left( {3{\rm{a}} - 3{\rm{x}}} \right) \le \frac{{\sqrt 3 }}{{12}}.4{{\rm{a}}^2} = \frac{{{a^2}\sqrt 3 }}{3} \Rightarrow {S_{MNPQ}} \le \frac{{{a^2}\sqrt 3 }}{3}\]
Dấu “=” xảy ra khi và chỉ khi \[3{\rm{x}} + a = 3{\rm{a}} - 3{\rm{x}} \Leftrightarrow x = \frac{2}{3}a\]
Vậy, diện tích thiết diện MNPQ đạt giá trị lớn nhất \[\frac{{{a^2}\sqrt 3 }}{3}\] khi và chỉ khi M nằm trên cạnh AB sao cho \[AM = \frac{2}{3}a\].


