Câu hỏi:
03/04/2024 26
Giải các phương trình sau:
a) \(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0\)
Giải các phương trình sau:
a) \(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0\)
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Tìm ĐKXĐ
- Sử dụng công thức \(\frac{1}{{{{\sin }^2}x}} = 1 + {\cot ^2}x\), biến đổi phương trình về dạng phương trình bậc hai đối với \(\cot x\).
Cách giải:
ĐKXĐ: \(\sin x \ne 0 \Leftrightarrow x \ne k\pi ,\,k \in \mathbb{Z}\)
Ta có:
\(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0 \Leftrightarrow 3\left( {1 + {{\cot }^2}x} \right) - 2\sqrt 3 \cot x - 6 = 0\)
\( \Leftrightarrow 3{\cot ^2}x - 2\sqrt 3 \cot x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}\cot x = \sqrt 3 \\\cot x = - \frac{1}{{\sqrt 3 }}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{3} + k\pi \end{array} \right.,\,k \in \mathbb{Z}\) (thỏa mãn ĐKXĐ)
Vậy phương trình đã cho có nghiệm \(x = \frac{\pi }{6} + k\pi ,\,x = - \frac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\,\).
Phương pháp:
- Tìm ĐKXĐ
- Sử dụng công thức \(\frac{1}{{{{\sin }^2}x}} = 1 + {\cot ^2}x\), biến đổi phương trình về dạng phương trình bậc hai đối với \(\cot x\).
Cách giải:
ĐKXĐ: \(\sin x \ne 0 \Leftrightarrow x \ne k\pi ,\,k \in \mathbb{Z}\)
Ta có:
\(\frac{3}{{{{\sin }^2}x}} - 2\sqrt 3 \cot x - 6 = 0 \Leftrightarrow 3\left( {1 + {{\cot }^2}x} \right) - 2\sqrt 3 \cot x - 6 = 0\)
\( \Leftrightarrow 3{\cot ^2}x - 2\sqrt 3 \cot x - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}\cot x = \sqrt 3 \\\cot x = - \frac{1}{{\sqrt 3 }}\end{array} \right.\)
\( \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{6} + k\pi \\x = - \frac{\pi }{3} + k\pi \end{array} \right.,\,k \in \mathbb{Z}\) (thỏa mãn ĐKXĐ)
Vậy phương trình đã cho có nghiệm \(x = \frac{\pi }{6} + k\pi ,\,x = - \frac{\pi }{3} + k\pi ,\,\,k \in \mathbb{Z}\,\).
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
a) Gọi a, b, c lần lượt là hệ số của các số hạng chứa \[{x^2}\], số hạng chứa \[{x^4}\], số hạng chứa \[{x^6}\] trong khai triển biểu thức \[{\left( {\frac{x}{2} - 4m} \right)^{12}}\] thành đa thức. Tìm m để \[a = bc\].
Câu 2:
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Gọi M, N lần lượt là trung điểm của AD và BC. Giao tuyến của hai mặt phẳng (SMN) và (SAC) là đường thẳng nào:
Câu 3:
Từ một hộp chứa 16 thẻ được đánh số từ 1 đến 16, chọn ngẫu nhiên 4 thẻ. Tính xác suất để 4 thẻ được chọn đều là số chẵn.
Câu 4:
Trong hệ trục tọa độ Oxy, cho đường tròn (C) có phương trình \({\left( {x - 2} \right)^2} + {\left( {y - 2} \right)^2} = 4\). Hỏi phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm O tỉ số \(k = \frac{1}{2}\) và phép quay tâm O góc quay \(180^\circ \) sẽ biến đường tròn (C) thành đường tròn nào trong các đường tròn có phương trình sau:
Câu 5:
Có hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,6. Xác suất để có ít nhất một người bắn trúng là:
Câu 6:
Một lớp học có 30 học sinh được xếp thành một hàng dọc. Tính xác suất để hai bạn An và Hà đứng cạnh nhau?
Câu 7:
Tập giá trị của hàm số \(y = \frac{{2\sin 2{\rm{x}} + \cos 2x}}{{\sin 2x - \cos 2x + 3}}\) có tất cả bao nhiêu giá trị nguyên?
Câu 8:
Cho tứ diện ABCD. Gọi M, N, P lần lượt là trung điểm của AB, BC, CD. Thiết diện của tứ diện cắt bởi mp(MNP) là hình gì trong các hình sau?
Câu 9:
b) \(\frac{{\cos \left( {\frac{{7\pi }}{2} - 2x} \right) - \sqrt 3 \cos \left( {2x - 3\pi } \right) + 2\cos x}}{{1 - 2\sin x}} = 0\)
Câu 10:
Tập xác định của hàm số \(y = \sqrt[3]{{\sin 2{\rm{x}} - \tan x}}\) là:
Câu 11:
b) Lớp 11A có 10 học sinh nữ và một số học sinh nam. Cần chọn 5 học sinh tham gia đội văn nghệ của trường. Biết xác suất cả 5 học sinh được chọn toàn nam bằng \[\frac{7}{{15}}\] xác suất để trong 5 học sinh được chọn 2 nữ. Hỏi lớp 11A có bao nhiêu học sinh?
Câu 12:
Có bao nhiêu cách chọn 6 học sinh đổi trực nhật từ một lớp 50 học sinh?
Câu 13:
Một đa giác lồi có 35 đường chéo. Hỏi đa giác đó có bao nhiêu đỉnh?
Câu 14:
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?
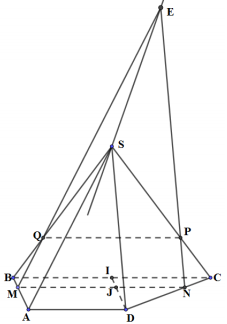
Cho hình chóp S.ABCD có đáy là hình thang ABCD với đáy lớn \(BC = 2{\rm{a}}\) và \(A{\rm{D}} = AB = a\). Mặt bên SAD là tam giác đều. Gọi M là điểm bất kì thuộc cạnh AB. Mặt phẳng \(\left( \alpha \right)\) đi qua M và song song với SA, BC, cắt CD, SC, SB lần lượt tại N, P, Q.
a) Chứng minh: \(PN//\left( {SA{\rm{D}}} \right)\).
b) Gọi E là giao điểm của MQ và NP. Chứng minh rằng E luôn nằm trên một đường thẳng cố định.
c) Giả sử \(AM = x\,\left( {0 < x < a} \right)\). Tính diện tích thiết diện tạo bởi mặt phẳng \(\left( \alpha \right)\) với hình chóp S.ABCD theo a và x. Tìm vị trí của M để thiết diện đạt giá trị lớn nhất?



