Câu hỏi:
03/04/2024 86
Cho phương trình \[\left( {2m + 1} \right){\cos ^2}2x - \left( {3m - 1} \right)\sin 2x - 3m + 1 = 0\] (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình có đúng hai nghiệm phân biệt thuộc \[\left( { - \pi ;\pi } \right)\].
A. 2
B. 4
C. 5
D. 3
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
Đặt ẩn phụ, tìm nghiệm phương trình bậc 2 rồi tìm m.
Cách giải:
Ta có \[\left( {2m + 1} \right){\cos ^2}2x - \left( {3m - 1} \right)\sin 2x - 3m + 1 = 0\] \[\left( * \right)\].
Đặt \(t = \sin 2x \Rightarrow - 1 \le t \le 1\left( {x \in \left( { - \pi ;\pi } \right)} \right)\)
Khi đó phương trình \[\left( * \right)\] có dạng:
\[\left( {2m + 1} \right)\left( {1 - {t^2}} \right) - \left( {3m - 1} \right)t - 3m + 1 = 0\]
\[ \Leftrightarrow \left( {2m + 1} \right){t^2} + \left( {3m - 1} \right)t + m - 2 = 0\]
\[ \Leftrightarrow \left( {t + 1} \right)\left( {\left( {2m + 1} \right)t + m - 2} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}t = - 1\\\left( {2m + 1} \right)t + m - 2 = 0\end{array} \right.\]
Nếu: \(t = - 1\left( {tm} \right) \Rightarrow \sin 2x = - 1\)
\( \Leftrightarrow 2x = \frac{{ - \pi }}{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow x = \frac{{ - \pi }}{4} + k\pi \in \left( { - \pi ;\pi } \right)\)
\( \Rightarrow \frac{{ - 3}}{4} < k < \frac{5}{4} \Rightarrow k \in \left\{ {0;1} \right\}\)
Khi đó phương trình \[\left( * \right)\] có 2 nghiệm phân biệt là \(\frac{{ - \pi }}{4}\); \(\frac{{3\pi }}{4}\)
+) \(\left( {2m + 1} \right)t = 2 - m\) \(\left( 1 \right)\).
Nếu \(m = \frac{{ - 1}}{2}\); \(\left( 1 \right) \Rightarrow m = 2\left( {ktm} \right)\)
\( \Rightarrow m \ne \frac{{ - 1}}{2} \Rightarrow t = \frac{{2 - m}}{{2m + 1}}\)
Để phương trình \[\left( * \right)\] có 2 nghiệm phân biệt thì
\(\left[ \begin{array}{l}t = \frac{{2 - m}}{{2m + 1}} = - 1\\t < - 1\\t > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 3\\\frac{{m + 3}}{{2m + 1}} < 0 \Leftrightarrow - 3 < m < \frac{{ - 1}}{2} \Leftrightarrow m \in \left\{ { - 2; - 1} \right\}\\\frac{{3m - 1}}{{2m + 1}} < 0 \Leftrightarrow \frac{{ - 1}}{2} < m < \frac{1}{3} \Leftrightarrow m = 0\end{array} \right.\)
Vậy có 4 giá trị của m thỏa mãn.
Đáp án B
Phương pháp:
Đặt ẩn phụ, tìm nghiệm phương trình bậc 2 rồi tìm m.
Cách giải:
Ta có \[\left( {2m + 1} \right){\cos ^2}2x - \left( {3m - 1} \right)\sin 2x - 3m + 1 = 0\] \[\left( * \right)\].
Đặt \(t = \sin 2x \Rightarrow - 1 \le t \le 1\left( {x \in \left( { - \pi ;\pi } \right)} \right)\)
Khi đó phương trình \[\left( * \right)\] có dạng:
\[\left( {2m + 1} \right)\left( {1 - {t^2}} \right) - \left( {3m - 1} \right)t - 3m + 1 = 0\]
\[ \Leftrightarrow \left( {2m + 1} \right){t^2} + \left( {3m - 1} \right)t + m - 2 = 0\]
\[ \Leftrightarrow \left( {t + 1} \right)\left( {\left( {2m + 1} \right)t + m - 2} \right) = 0\]
\[ \Leftrightarrow \left[ \begin{array}{l}t = - 1\\\left( {2m + 1} \right)t + m - 2 = 0\end{array} \right.\]
Nếu: \(t = - 1\left( {tm} \right) \Rightarrow \sin 2x = - 1\)
\( \Leftrightarrow 2x = \frac{{ - \pi }}{2} + k2\pi \left( {k \in \mathbb{Z}} \right)\)
\( \Leftrightarrow x = \frac{{ - \pi }}{4} + k\pi \in \left( { - \pi ;\pi } \right)\)
\( \Rightarrow \frac{{ - 3}}{4} < k < \frac{5}{4} \Rightarrow k \in \left\{ {0;1} \right\}\)
Khi đó phương trình \[\left( * \right)\] có 2 nghiệm phân biệt là \(\frac{{ - \pi }}{4}\); \(\frac{{3\pi }}{4}\)
+) \(\left( {2m + 1} \right)t = 2 - m\) \(\left( 1 \right)\).
Nếu \(m = \frac{{ - 1}}{2}\); \(\left( 1 \right) \Rightarrow m = 2\left( {ktm} \right)\)
\( \Rightarrow m \ne \frac{{ - 1}}{2} \Rightarrow t = \frac{{2 - m}}{{2m + 1}}\)
Để phương trình \[\left( * \right)\] có 2 nghiệm phân biệt thì
\(\left[ \begin{array}{l}t = \frac{{2 - m}}{{2m + 1}} = - 1\\t < - 1\\t > 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 3\\\frac{{m + 3}}{{2m + 1}} < 0 \Leftrightarrow - 3 < m < \frac{{ - 1}}{2} \Leftrightarrow m \in \left\{ { - 2; - 1} \right\}\\\frac{{3m - 1}}{{2m + 1}} < 0 \Leftrightarrow \frac{{ - 1}}{2} < m < \frac{1}{3} \Leftrightarrow m = 0\end{array} \right.\)
Vậy có 4 giá trị của m thỏa mãn.CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Gieo một con xúc xắc cân đối, đồng chất hai lần. Gọi A là biến cố “tổng số chấm xuất hiện trên mặt của xúc sắc sau hai lần gieo bằng 8”. Khi đó xác suất của biến cố A là bao nhiêu?
Câu 2:
Cho đa giác đều 12 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 12 đỉnh của đa giác. Xác suất để 3 đỉnh được chọn tạo thành tam giác đều là:
Câu 3:
Cho \[P\left( x \right) = {\left( {x - 2y} \right)^5}\]. Khai triển \[P\left( x \right)\] thành đa thức ta có :
Câu 4:
Cho phương trình \[ - \sqrt {2 - m} \sin x + \left( {m + 1} \right)\cos x = m - 1\]. Tìm tất cả các giá trị thực của m để phương trình có nghiệm.
Câu 5:
Cho hình chóp S.ABCD, đáy ABCD là tứ giác có các cạnh đối diện không song song. Lấy điểm M thuộc miền trong tam giác SCD. Tìm giao tuyến của hai mặt phẳng \(\left( {ABM} \right)\) và \(\left( {SCD} \right)\).
Câu 6:
Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, SC, OB. Gọi Q là giao điểm của SD với mp \(\left( {MNP} \right)\). Tính \[\frac{{SQ}}{{SD}}\].
Câu 7:
Phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) biến mỗi điểm M thành điểm \(M'\) sao cho
Câu 8:
Tổ 1 lớp 11A có 6 nam 7 nữ, tổ 2 có 5 nam, 8 nữ. Chọn ngẫu nhiên mỗi tổ một học sinh. Xác suất để 2 học sinh được chọn đều là nữ là:
Câu 9:
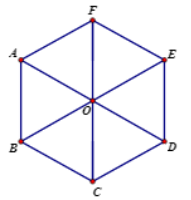
Cho lục giác đều ABCDEF tâm (như hình vẽ). Phép tịnh tiến theo véctơ \(\overrightarrow {BC} \) biến hình thoi ABOF thành hình thoi nào sau đây?