Câu hỏi:
03/04/2024 70
Cho các mệnh đề sau:
(I): Hàm số y=sinx có chu kì là π2.
(II): Hàm số y=tanx có tập giá trị là R∖{π2+kπ|k∈Z}.
(III): Đồ thị hàm số y=cosx đối xứng qua trục tung.
(IV): Hàm số y=cotx đồng biến trên (−π;0).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
Cho các mệnh đề sau:
(I): Hàm số y=sinx có chu kì là π2.
(II): Hàm số y=tanx có tập giá trị là R∖{π2+kπ|k∈Z}.
(III): Đồ thị hàm số y=cosx đối xứng qua trục tung.
(IV): Hàm số y=cotx đồng biến trên (−π;0).
Có bao nhiêu mệnh đề đúng trong các mệnh đề trên?
A. 2.
Đáp án chính xác
B. 4.
C. 1.
D. 3.
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Phương pháp:
Nhận xét từng mệnh đề rồi kết luận.
Cách giải:
Hàm số y=sinx có chu kỳ là 2π nên I sai.
Hàm số y=tanx xác định khi cosx≠0⇔x≠π2+kπ(k∈Z) nên II đúng.
Ta có hàm số y=cosx có y(x)=y(−x) nên đồ thị hàm số đối xứng với nhau qua trục tung nên III đúng.
Hàm số y=cotx luôn nghịch biến trên R nên IV sai.
Đáp án A
Phương pháp:
Nhận xét từng mệnh đề rồi kết luận.
Cách giải:
Hàm số y=sinx có chu kỳ là 2π nên I sai.
Hàm số y=tanx xác định khi cosx≠0⇔x≠π2+kπ(k∈Z) nên II đúng.
Ta có hàm số y=cosx có y(x)=y(−x) nên đồ thị hàm số đối xứng với nhau qua trục tung nên III đúng.
Hàm số y=cotx luôn nghịch biến trên R nên IV sai.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Gieo một con xúc xắc cân đối, đồng chất hai lần. Gọi A là biến cố “tổng số chấm xuất hiện trên mặt của xúc sắc sau hai lần gieo bằng 8”. Khi đó xác suất của biến cố A là bao nhiêu?
Xem đáp án »
03/04/2024
203
Câu 2:
Cho phương trình −√2−msinx+(m+1)cosx=m−1. Tìm tất cả các giá trị thực của m để phương trình có nghiệm.
Xem đáp án »
03/04/2024
134
Câu 3:
Cho đa giác đều 12 đỉnh. Chọn ngẫu nhiên 3 đỉnh trong 12 đỉnh của đa giác. Xác suất để 3 đỉnh được chọn tạo thành tam giác đều là:
Xem đáp án »
03/04/2024
132
Câu 5:
Cho hình chóp S.ABCD, đáy ABCD là tứ giác có các cạnh đối diện không song song. Lấy điểm M thuộc miền trong tam giác SCD. Tìm giao tuyến của hai mặt phẳng (ABM) và (SCD).
Xem đáp án »
03/04/2024
125
Câu 6:
Trong mặt phẳng cho 2019 điểm phân biệt. Hỏi có tất cả bao nhiêu vectơ khác vectơ không mà có điểm đầu và điểm cuối thuộc 2019 điểm trên?
Xem đáp án »
03/04/2024
122
Câu 7:
Phép vị tự tâm O tỉ số k (k≠0) biến mỗi điểm M thành điểm M′ sao cho
Xem đáp án »
03/04/2024
120
Câu 8:
Cho hình chóp S.ABCD đáy là hình bình hành tâm O. Gọi M, N, P lần lượt là trung điểm của SA, SC, OB. Gọi Q là giao điểm của SD với mp (MNP). Tính SQSD.
Xem đáp án »
03/04/2024
114
Câu 9:
Cho phương trình (2m+1)cos22x−(3m−1)sin2x−3m+1=0 (m là tham số thực). Có tất cả bao nhiêu giá trị nguyên của m để phương trình có đúng hai nghiệm phân biệt thuộc (−π;π).
Xem đáp án »
03/04/2024
114
Câu 10:
Tổ 1 lớp 11A có 6 nam 7 nữ, tổ 2 có 5 nam, 8 nữ. Chọn ngẫu nhiên mỗi tổ một học sinh. Xác suất để 2 học sinh được chọn đều là nữ là:
Xem đáp án »
03/04/2024
106
Câu 11:
Một cầu thủ sút bóng vào cầu môn hai lần độc lập nhau. Biết rằng xác suất sút trúng vào cầu môn của cầu thủ đó là 0,7. Xác suất sao cho cầu thủ đó sút một lần trượt và một lần trúng cầu môn là:
Xem đáp án »
03/04/2024
106
Câu 12:
Cho lục giác đều ABCDEF tâm (như hình vẽ). Phép tịnh tiến theo véctơ →BC biến hình thoi ABOF thành hình thoi nào sau đây?
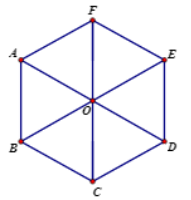

Xem đáp án »
03/04/2024
104
Câu 13:
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là một điểm trên cạnh BC sao cho MB=2MC. Khẳng định nào sau đây đúng?
Xem đáp án »
03/04/2024
101
Câu 14:
Trong hệ trục tọa độ Oxy cho M(3;−4); N(0;−2). Phép vị tự tâm I(−3;4) tỷ số –2 biến điểm M thành M′ và điểm N thành N′. Khi đó độ dài đoạn M′N′ bằng bao nhiêu?
Xem đáp án »
03/04/2024
97
Câu 15:
Gieo một đồng xu đồng có hai mặt sấp và ngửa cân đối đồng chất 5 lần. khi đó số phần tử của không gian mẫu nΩ bằng bao nhiêu?
Xem đáp án »
03/04/2024
97


