Giải SGK Toán 7 Bài 7 (Chân trời sáng tạo): Tính chất ba đường trung tuyến của tam giác

Giải SGK Toán 7 Bài 7: Tính chất ba đường trung tuyến của tam giác

A. Các câu hỏi trong bài

Giải Toán 7 trang 73 Tập 2

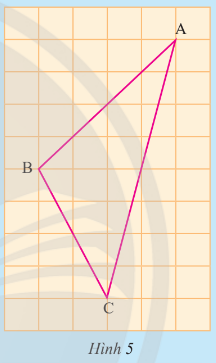
Khởi động trang 73 Toán 7 Tập 2:

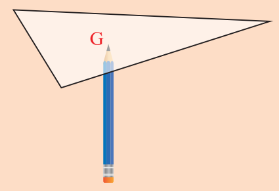
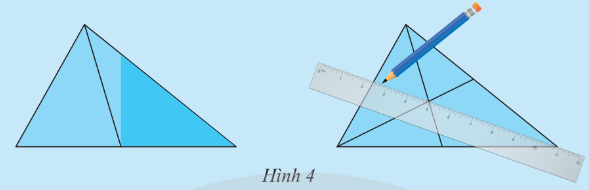
Đặt đầu bút chì ở điểm nào của tam giác thì ta có thể giữ tấm bìa thăng bằng?

Lời giải:

Sau bài học này chúng ta sẽ trả lời được câu hỏi trên như sau:

Để giữ được tấm bìa thăng bằng thì ta đặt đầu bút chì tại trọng tâm của tam giác.

Khám phá 1 trang 73 Toán 7 Tập 2:

Vẽ tam giác ABC, xác định trung điểm D của cạnh BC và vẽ đoạn thẳng nối hai điểm A và D.

Lời giải:

Cách vẽ:

– Vẽ tam giác ABC bất kỳ.

– Lấy trung điểm D của cạnh BC.

– Nối A và D ta được đoạn thẳng AD.

Ta có hình vẽ sau:

Thực hành 1 trang 73 Toán 7 Tập 2:

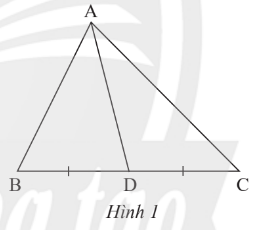
Em hãy vẽ tiếp các đường trung tuyến còn lại của tam giác ABC (Hình 1).

Lời giải:

Gọi E và F lần lượt là trung điểm của AC và AB.

Nối BE và CF ta được hai đường trung tuyến còn lại của tam giác ABC.

Ta có hình vẽ sau:

Vận dụng 1 trang 73 Toán 7 Tập 2:

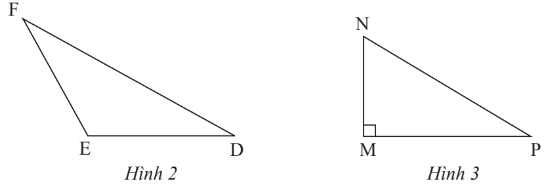
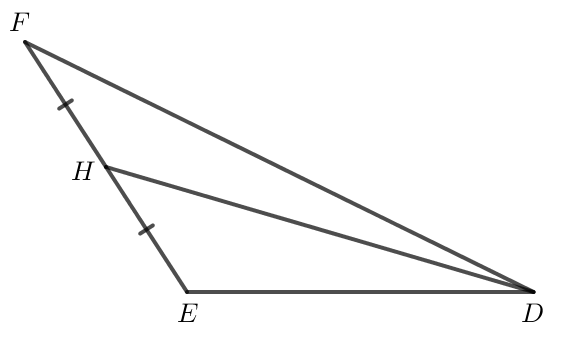
a) Vẽ đường trung tuyến DH của tam giác DEF (Hình 2).

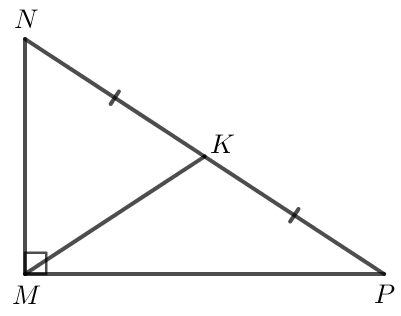
b) Vẽ đường trung tuyến MK của tam giác vuông MNP (Hình 3).

c) Vẽ tam giác nhọn IJK và tất cả các đường trung tuyến của nó.

Lời giải:

a) Vì DH là đường trung tuyến của tam giác DEF nên H là trung điểm của EF.

Ta có hình vẽ sau:

b) Vì MK là đường trung tuyến của tam giác MNP nên K là trung điểm của NP.

Ta có hình vẽ sau:

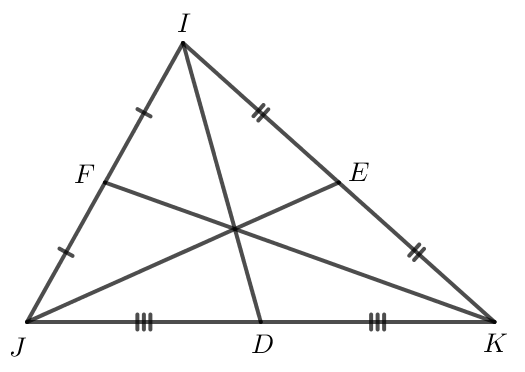
c) Gọi D, E, F lần lượt là trung điểm của các cạnh JK, KI, IJ.

Nối ID, JE, KF ta được ba đường trung tuyến của tam giác IJK.

Ta có hình vẽ sau:

Giải Toán 7 trang 74 Tập 2

Khám phá 2 trang 74 Toán 7 Tập 2:

a) Cắt một tam giác bằng giấy. Gấp lại để xác định trung điểm một cạnh của nó. Kẻ đoạn thẳng nối trung điểm này với đỉnh đối diện (Hình 4). Bằng cách tương tự, hãy vẽ tiếp hai đường trung tuyến còn lại.

Quan sát tam giác trên hình, em thấy ba đường trung tuyến vừa vẽ có cùng đi qua một điểm hay không?

b) Em hãy đếm ô rồi vẽ lại tam giác ABC trong Hình 5 vào giấy kẻ ô vuông. Vẽ hai đường trung tuyến BE và CF của tam giác ABC. Hai đường trung tuyến này cắt nhau tại G. Tia AG cắt BC tại D.

Em hãy quan sát và cho biết:

• AD có phải là đường trung tuyến của tam giác ABC không?

• Các tỉ số $\frac{BG}{BE}$, $\frac{CG}{CF}$, $\frac{AG}{AD}$ bằng bao nhiêu?

Lời giải:

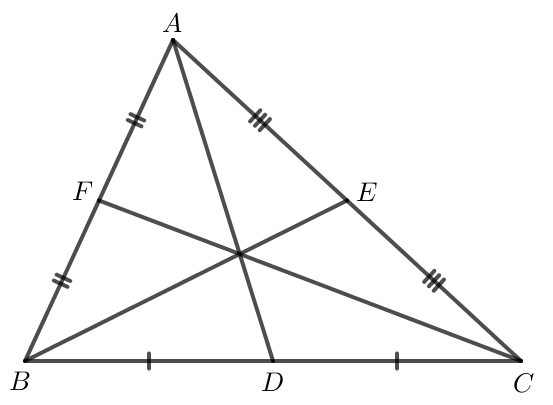
a) Thực hiện theo yêu cầu của bài toán ta thu được hình sau:

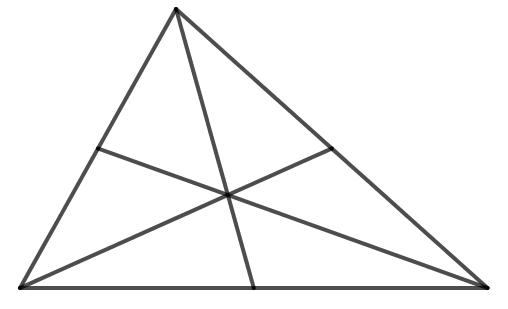
Ta thấy ba đường trung tuyến cùng đi qua một điểm.

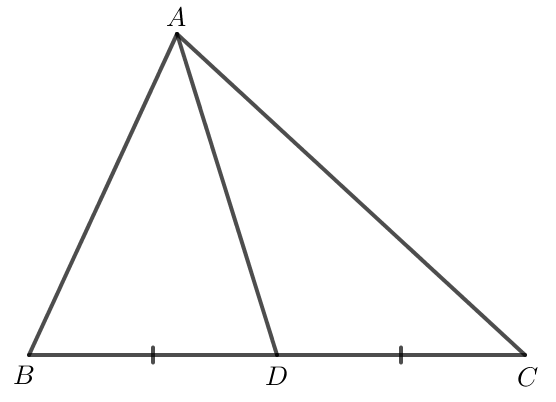
b) Ta có hình vẽ sau:

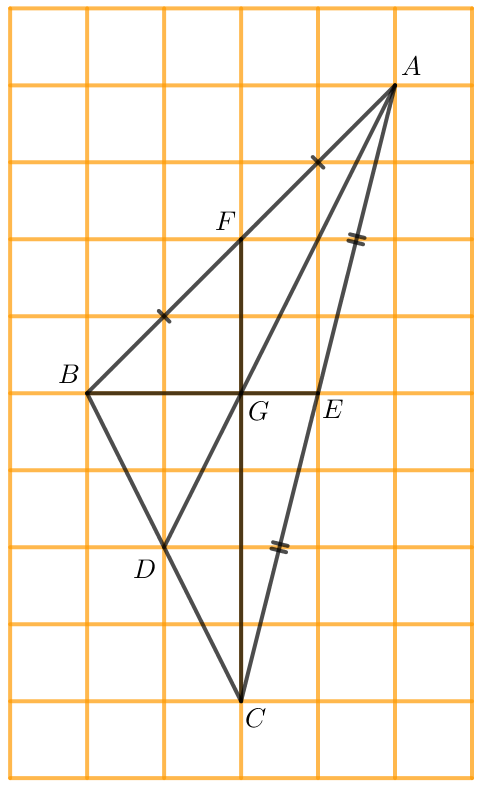
• Trong hình vẽ trên, ta thấy D là trung điểm của BC nên AD là đường trung tuyến của tam giác ABC.

• $\frac{BG}{BE}=\frac{2}{3}$; $\frac{CG}{CF}=\frac{4}{6}=\frac{2}{3}$; $\frac{AG}{AD}=\frac{4}{6}=\frac{2}{3}$.

Giải Toán 7 trang 75 Tập 2

Thực hành 2 trang 75 Toán 7 Tập 2:

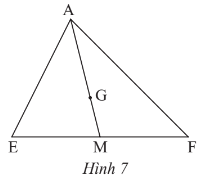
Trong Hình 7, G là trọng tâm của tam giác AEF với đường trung tuyến AM.

Hãy tính các tỉ số:

a) $\frac{GM}{AM}$;                       b) $\frac{GM}{AG}$;                       c) $\frac{AG}{GM}$.

Lời giải:

a) Vì G là trọng tâm của tam giác ABC nên AG = $\frac{2}{3}$AM.

Khi đó: GM = AM - AG = AM - $\frac{2}{3}$AM = $\frac{1}{3}$AM.

Do đó $\frac{GM}{AM}=\frac{1}{3}$.

b) Ta có GM = $\frac{1}{3}$AM và AG = $\frac{2}{3}$AM.

Suy ra GM : AG = $\frac{1}{3}$AM : $\frac{2}{3}$AM = $\frac{1}{2}$.

Do đó $\frac{GM}{AG}=\frac{1}{2}$.

c) Vì $\frac{GM}{AG}=\frac{1}{2}$ nên $\frac{AG}{GM}$ = 2.

Vận dụng 2 trang 75 Toán 7 Tập 2:

Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm các tam giác ABC và DBC. Chứng minh rằng AI = IJ = JD.

Lời giải:

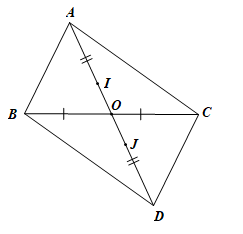
Theo đề bài, O là trung điểm của BC nên AO là đường trung tuyến của ∆ABC, DO là đường trung tuyến của ∆DBC.

Vì I là trọng tâm của ∆ABC nên I nằm trên AO sao cho AI = $\frac{2}{3}$ AO.

Vì J là trọng tâm của ∆DBC nên J nằm trên DO sao cho DJ = $\frac{2}{3}$DO.

Mà OA và OD là hai tia đối nhau nên A, I, O, J, D thẳng hàng.

Vì AI = $\frac{2}{3}$AO nên OI = $\frac{1}{3}$AO.

Vì DJ = $\frac{2}{3}$DO nên OJ = $\frac{1}{3}$DO.

Ta có AO = DO và ba điểm I, O, J thẳng hàng.

Suy ra IJ = OI + OJ = $\frac{1}{3}$AO + $\frac{1}{3}$DO = $\frac{2}{3}$AO.

Khi đó AI = $\frac{2}{3}$AO, IJ = $\frac{2}{3}$AO, DJ = $\frac{2}{3}$AO.

Do đó AI = IJ = JD.

B. Bài tập

Bài 1 trang 75 Toán 7 Tập 2:

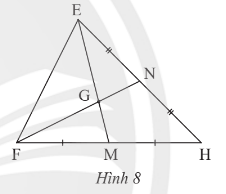
Quan sát Hình 8. Thay $\boxed{?}$ bằng số thích hợp.

EG = $\boxed{?}$EM;          GM = $\boxed{?}$EM;            GM = $\boxed{?}$EG;

FG = $\boxed{?}$GN;            FN = $\boxed{?}$ GN;            FN = $\boxed{?}$FG.

Lời giải:

Trên Hình 8 có: M và N lần lượt là trung điểm của HF và HE.

Suy ra HF và HE là hai đường trung tuyến của ∆EHF

Mà HF và HE cắt nhau tại G.

Nên G là giao điểm hai đường trung tuyến của ∆EFH.

Do đó G là trọng tâm của ∆EFH.

Khi đó:

• EG = $\frac{2}{3}$EM nên GM = EM - EG = EM - $\frac{2}{3}$EM = $\frac{1}{3}$EM.

Suy ra GM : EG = $\frac{1}{3}$EM : $\frac{2}{3}$EM = $\frac{1}{2}$ hay GM = $\frac{1}{2}$EG.

• FG = $\frac{2}{3}$FN nên GN = FN - FG = FN - $\frac{2}{3}$FN = $\frac{1}{3}$FN.

Suy ra FG : GN = $\frac{2}{3}$FN : $\frac{1}{3}$FN = 2 hay FG = 2GN.

Do GN = $\frac{1}{3}$FN nên FN = 3GN.

Do FG = $\frac{2}{3}$FN nên FN = $\frac{3}{2}$FG.

Ta điền như sau:

EG = $\frac{2}{3}$EM; GM = $\frac{1}{3}$EM; GM = $\frac{1}{2}$EG;

FG = 2GN; FN = 3GN; FN = $\frac{3}{2}$FG.

Bài 2 trang 75 Toán 7 Tập 2:

Quan sát Hình 9.

a) Biết AM = 15 cm, tính AG.

b) Biết GN = 6 cm, tính CN.

Lời giải:

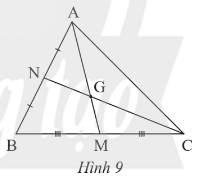
a) Ta có G là giao điểm hai đường trung tuyến của ∆ABC nên G là trọng tâm của ∆ABC.

Do đó AG = $\frac{2}{3}$AM = $\frac{2}{3}$ . 15 = 10 (cm).

Vậy AG = 10 cm.

b) Vì G là trọng tâm của ∆ABC nên GN = $\frac{1}{3}$CN.

Do đó CN = 3GN = 3.6 = 18 (cm).

Vậy CN = 18 cm.

Bài 3 trang 75 Toán 7 Tập 2:

Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia AM lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI.

Lời giải:

Note: Đề chưa chính xác.

Đề đúng:

“Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia MA lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là trung điểm của BE, AI cắt BG tại F. Chứng minh rằng AF = 2FI.”

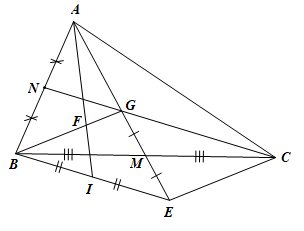
a) Xét ∆BMG và ∆CME có:

MG = ME (giả thiết);

$\widehat{BMG}=\widehat{CME}$ (đối đỉnh);

BM = CM (do M là trung điểm của BC).

Do đó ∆BMG = ∆CME (c.g.c).

Suy ra $\widehat{BGM}=\widehat{CEM}$ (hai góc tương ứng).

Mà hai góc này ở vị trí so le trong nên BG // EC.

b) Vì G là trọng tâm của ∆ABC nên AG = 2GM.

Ta có ME = GM và G, M, E thẳng hàng nên GE = GM + ME = 2GM.

Suy ra AG = GE nên G là trung điểm của AE.

Xét ∆ABE có hai đường trung tuyến AI và BG cắt nhau tại F nên F là trọng tâm của ∆ABE.

Do đó AF = 2FI.

Bài 4 trang 75 Toán 7 Tập 2:

Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.

a) Chứng minh rằng BM = CN.

b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC.

Lời giải:

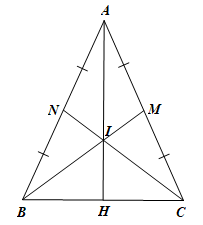
a) Vì ∆ABC cân tại A nên AB = AC và $\widehat{ABC}=\widehat{ACB}$.

Ta có BM và CN là các đường trung tuyến của ∆ABC.

Nên M và N là lần lượt là trung điểm của AC và AB.

Khi đó AN = $\frac{1}{2}$AB; AM = $\frac{1}{2}$AC.

Mà AB = AC nên AN = AM.

Xét ∆AMB và ∆ANC có:

AM = AN (chứng minh trên);

$\widehat{MAN}$ là góc chung;

AB = AC (chứng minh trên).

Do đó ∆AMB = ∆ANC (c.g.c).

Suy ra BM = NC (hai cạnh tương ứng).

b) Ta có ∆ABC có hai đường trung tuyến BM và CN cắt nhau tại I nên I là trọng tâm của ∆ABC.

Suy ra AI đi qua trung điểm của BC.

Mà AI cắt BC tại H nên H là trung điểm của BC.

Giải Toán 7 trang 76 Tập 2

Bài 5 trang 76 Toán 7 Tập 2:

Cho tam giác ABC có đường trung tuyến BM bằng trung tuyến CN. Chứng minh rằng tam giác ABC cân.

Lời giải:

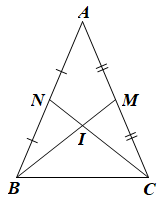
Gọi I là giao điểm của BM và CN.

Xét ∆ABC có I là giao điểm hai đường trung tuyến nên I là trọng tâm của ∆ABC.

Khi đó BI = $\frac{2}{3}$BM; IM = $\frac{1}{3}$BM; CI = $\frac{2}{3}$CN; IN = $\frac{1}{3}$CN.

Mà BM = CN nên BI = CI; IM = IN.

Xét ∆NIB và ∆MIC có:

IN = IM (chứng minh trên);

$\widehat{NIB}=\widehat{MIC}$ (hai góc đối đỉnh);

IB = IC (chứng minh trên).

Do đó ∆NIB = ∆MIC (c.g.c).

Suy ra BN = CM (hai cạnh tương ứng).

Mà BN = $\frac{1}{2}$AB (do N là trung điểm của AB);

và CM = $\frac{1}{2}$AC (do M là trung điểm của AC)

Do đó AB = AC.

Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Bài 6 trang 76 Toán 7 Tập 2:

Cho tam giác ABC cân tại A có BE và CD là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.

Lời giải:

Ta có BE và CD là hai đường trung tuyến của tam giác ABC nên E và D lần lượt là trung điểm của AC, AB.

Suy ra AE = $\frac{1}{2}$AC; AD = $\frac{1}{2}$AB.

Mà AB = AC (do ∆ABC cân tại A) nên AE = AD.

Xét ∆ABE và ∆ACD có:

AB = AC (chứng minh trên);

$\widehat{A}$ là góc chung;

AE = AD (chứng minh trên).

Do đó ∆ABE = ∆ACD (c.g.c).

Suy ra BE = CD (hai cạnh tương ứng).

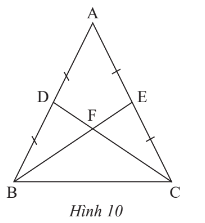
Ta có F là giao điểm hai đường trung tuyến BE và CD trong ∆ABC nên F là trọng tâm của ∆ABC.

Do đó DF = $\frac{1}{3}$CD = $\frac{1}{3}$BE = $\frac{1}{3}$. 9 = 3 (cm).

Vậy DF = 3 cm.

Xem thêm lời giải bài tập SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học