Giải SGK Toán 7 Bài 8: Tính chất ba đường cao của tam giác
A. Các câu hỏi trong bài
Giải Toán 7 trang 77 Tập 2
Khởi động trang 77 Toán 7 Tập 2:
Làm thế nào để tính khoảng cách từ mỗi đỉnh đến cạnh đối diện của một tam giác?
Lời giải:
Sau bài học này chúng ta sẽ giải quyết được câu hỏi trên như sau:
Ta có đường vuông góc kẻ từ đỉnh đến đường thẳng chứa cạnh đối diện là độ dài đường cao của tam giác.
Do đó để tính khoảng cách từ mỗi đỉnh đến cạnh đối diện của tam giác, ta tính độ dài đường cao xuất phát từ đỉnh đến cạnh đối diện của đỉnh đó trong tam giác.
Khám phá 1 trang 77 Toán 7 Tập 2:
Lời giải:
* Cách vẽ:
- Vẽ tam giác ABC.
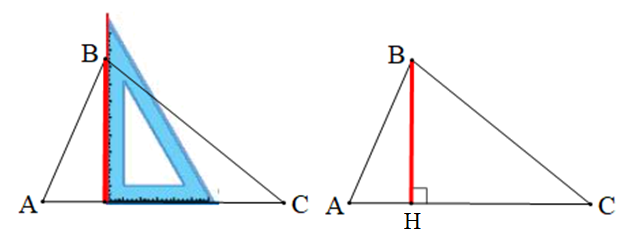
- Đặt thước êke sao cho một cạnh góc vuông của thước trùng với cạnh AC và cạnh còn lại đi qua đỉnh của B của tam giác.
- Kẻ đường thẳng BH dọc theo cạnh góc vuông còn lại của thước (H Î AC).
Khi đó, BH là đoạn thẳng vuông góc từ đỉnh B đến cạnh đối diện AC của tam giác.
Ta có hình vẽ sau:
Thực hành 1 trang 77 Toán 7 Tập 2:
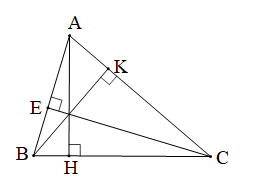
Vẽ ba đường cao AH, BK, CE của tam giác nhọn ABC.
Lời giải:
* Cách vẽ:
- Vẽ tam giác nhọn ABC.
- Từ ba điểm A, B, C lần lượt vẽ các đường vuông góc đến BC, AC, AB tại các điểm H, K, E.
Khi đó, AH, BK, CE là ba đường cao của tam giác nhọn ABC.
* Ta có hình vẽ sau:
Vận dụng 1 trang 77 Toán 7 Tập 2:
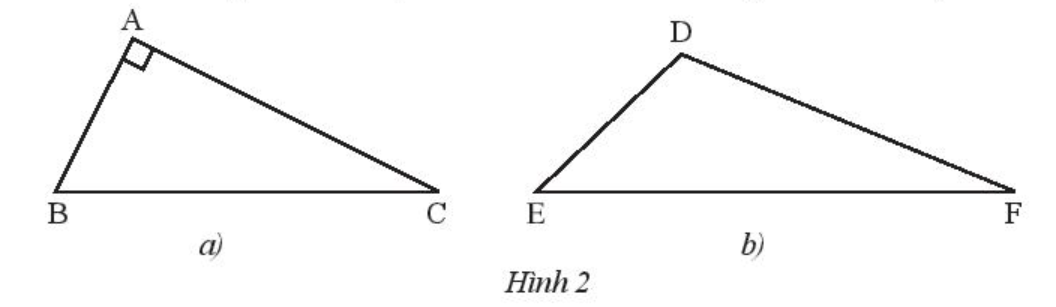
Vẽ đường cao xuất phát từ đỉnh B của tam giác vuông ABC (Hình 2a).
Vẽ đường cao xuất phát từ đỉnh F của tam giác tù DEF (Hình 2b).
Lời giải:
+) Hình 2a:
Tam giác ABC có ^BAC=90° nên BA AC.
Do đó đường cao xuất phát từ đỉnh B của tam giác vuông ABC là đường thẳng BA.
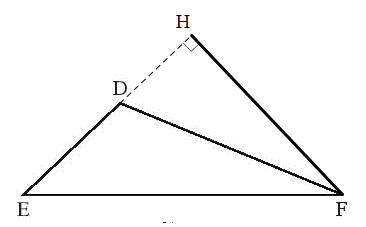
+) Hình 2b:
Ta kéo dài đường thẳng ED, từ F vẽ FH ED tại H, ta có FH là đường cao kẻ từ F đến DE.
Ta có hình vẽ sau:
Khám phá 2 trang 77 Toán 7 Tập 2:
Lời giải:
* Cách vẽ:
- Vẽ tam giác ABC.
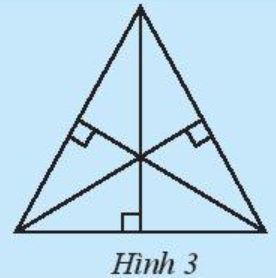
- Vẽ ba đường cao AH, BK, CI của tam giác ABC.
* Ta có hình vẽ:
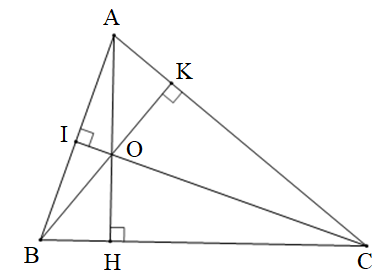
Vậy ba đường cao vừa vẽ cùng đi qua một điểm, điểm này là điểm O trong hình vẽ trên.
Giải Toán 7 trang 78 Tập 2
Thực hành 2 trang 78 Toán 7 Tập 2:
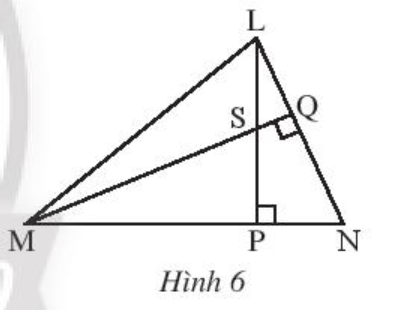
Cho tam giác LMN có hai đường cao LP và MQ cắt nhau tại S (Hình 6).
Chứng minh rằng NS vuông góc với ML.
Lời giải:
Do ∆LMN có hai đường cao LP và MQ cắt nhau tại S (giả thiết)
Nên S là trực tâm của ∆LMN.
Do đó NS ML.
Vận dụng 2 trang 78 Toán 7 Tập 2:
Lời giải:
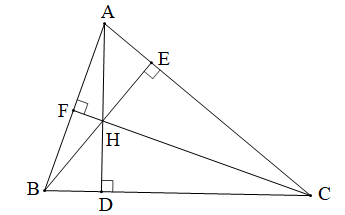
+) Tìm trực tâm của tam giác HBC:
Tam giác HBC có HD ⊥ BC, CE ⊥ HB
Do đó HD và CE là hai đường cao của tam giác HBC.
Mà HD và CE cắt nhau tại A nên A là trực tâm của tam giác HBC.
Vậy A là trực tâm của tam giác HBC.
+) Tìm trực tâm của tam giác HAB:
Tam giác HAB có HF ⊥ AB, BD ⊥ AH
Do đó HF, BD là hai đường cao của tam giác HAB.
Mà HF và BD cắt nhau tại C nên C là trực tâm của tam giác HAB.
Vậy C là trực tâm của tam giác HAB.
+) Tìm trực tâm của tam giác HAC:
Tam giác HAC có HE ⊥ AC, AF ⊥ HC
Do đó HE, AF là hai đường cao của tam giác HAC.
Mà HE và AF cắt nhau tại B nên B là trực tâm của tam giác HAC.
Vậy B là trực tâm của tam giác HAC.
B. Bài tập
Lời giải:
|
GT |
ABC vuông tại A; H thuộc cạnh AB; HM BC; tia MH cắt tia CA tại N. |
|
KL |
CH NB. |
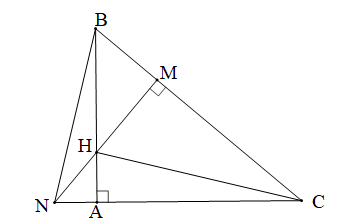
Xét tam giác BNC có: BA ⊥ NC, NM ⊥ BC
Do đó BA, NM là hai đường cao của tam giác BNC.
Mà BA và NM cắt nhau tại H nên H là trực tâm của tam giác BNC.
Do đó CH ⊥ NB.
Vậy CH ⊥ NB.
Lời giải:
|
GT |
ABC vuông tại A; M thuộc tia BA, BM = BC; AH là tia phân giác của góc B, H ∈ AC. |
|
KL |
MH BC. |
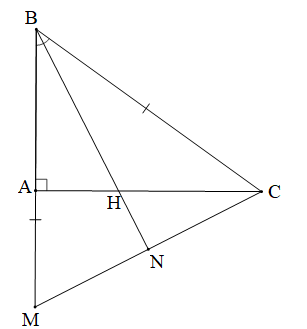
Gọi N là giao điểm của BH và MC.
Xét BMN và BCN có:
BM = BC (giả thiết),
(do BN là tia phân giác của góc B),
BN là cạnh chung,
Do đó BMN = BCN (c.g.c)
Suy ra (hai góc tương ứng)
Mà (hai góc kề bù)
Nên hay BN ⊥ MC.
Tam giác BMC có CA ⊥ BM (do CA ⊥ BA), BN ⊥ MC (chứng minh trên)
Do đó CA, BN là hai đường cao của tam giác BMC.
Mà CA và BN cắt nhau tại H nên H là trực tâm của tam giác BMC.
Do đó MH ⊥ BC.
Lời giải:
|
GT |
ABC vuông cân tại A, E thuộc cạnh AC, D thuộc tia đối của tia AB, AD = AE |
|
KL |
a) DE BC. b) BE DC. |
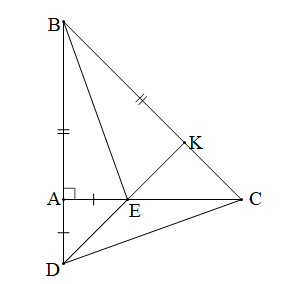
Gọi K là giao điểm của DE và BC.
Tam giác ABC vuông cân tại A (giả thiết) nên .
Tam giác ADE vuông tại A lại có có AD = AE (giả thiết) nên tam giác ADE vuông cân tại A.
Do đó .
Xét tam giác BDK có: (tổng số đo ba góc của một tam giác)
Suy ra
Hay
Do đó
Suy ra DK BC
Vậy DE BC.
b) Tam giác BDC có: CA BD, DK BC
Do đó CA, DK là hai đường cao của tam giác BDC.
Mà CA và DK cắt nhau tại E nên E là trực tâm của tam giác BDC.
Suy ra BE DC.
Vậy BE DC.
Lời giải:
|
GT |
ABC nhọn, AD, BE, CF là ba đường cao của tam giác, AD = BE = CF |
|
KL |
ABC đều. |
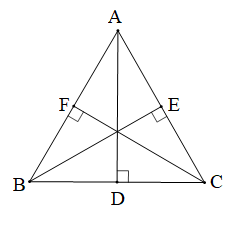
• Xét ∆FBC (vuông tại F) và ∆ECB (vuông tại E) có:
CF = BE (giả thiết);
BC là cạnh chung.
Do đó ∆FBC = ∆ECB (cạnh huyền - cạnh góc vuông).
Suy ra (hai góc tương ứng).
Hay
Khi đó tam giác ABC cân tại A.
Suy ra AB = AC (1).
• Tương tự ta cũng có ∆ABD = ∆BAE (cạnh huyền - cạnh góc vuông).
Suy ra (hai góc tương ứng).
Hay do đó tam giác ABC cân tại C.
Suy ra CA = CB (2).
Từ (1) và (2) ta có AB = BC = CA
Do đó tam giác ABC đều.
Vậy tam giác ABC đều.
Xem thêm lời giải bài tập SGK Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 6: Tính chất ba đường trung trực của tam giác
Bài 7: Tính chất ba đường trung tuyến của tam giác
Bài 9: Tính chất ba đường phân giác của tam giác
Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học