Cho tam giác ABC có đường trung tuyến BM bằng trung tuyến CN. Chứng minh rằng tam giác ABC cân

Bài 5 trang 76 Toán 7 Tập 2:

Cho tam giác ABC có đường trung tuyến BM bằng trung tuyến CN. Chứng minh rằng tam giác ABC cân.

Trả lời

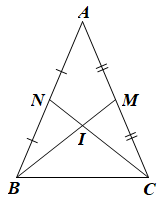
Gọi I là giao điểm của BM và CN.

Xét ∆ABC có I là giao điểm hai đường trung tuyến nên I là trọng tâm của ∆ABC.

Khi đó BI = $\frac{2}{3}$BM; IM = $\frac{1}{3}$BM; CI = $\frac{2}{3}$CN; IN = $\frac{1}{3}$CN.

Mà BM = CN nên BI = CI; IM = IN.

Xét ∆NIB và ∆MIC có:

IN = IM (chứng minh trên);

$\widehat{NIB}=\widehat{MIC}$ (hai góc đối đỉnh);

IB = IC (chứng minh trên).

Do đó ∆NIB = ∆MIC (c.g.c).

Suy ra BN = CM (hai cạnh tương ứng).

Mà BN = $\frac{1}{2}$AB (do N là trung điểm của AB);

và CM = $\frac{1}{2}$AC (do M là trung điểm của AC)

Do đó AB = AC.

Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: 

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác

Bài 7: Tính chất ba đường trung tuyến của tam giác

Bài 8: Tính chất ba đường cao của tam giác

Bài 9: Tính chất ba đường phân giác của tam giác

Bài 10: Hoạt động thực hành và trải nghiệm. Làm giàn hoa tam giác để trang trí lớp học