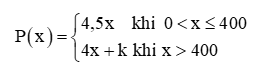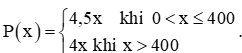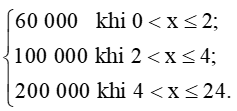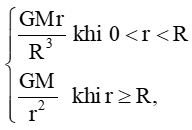Giải Toán 11 Bài 3: Hàm số liên tục
Lời giải:
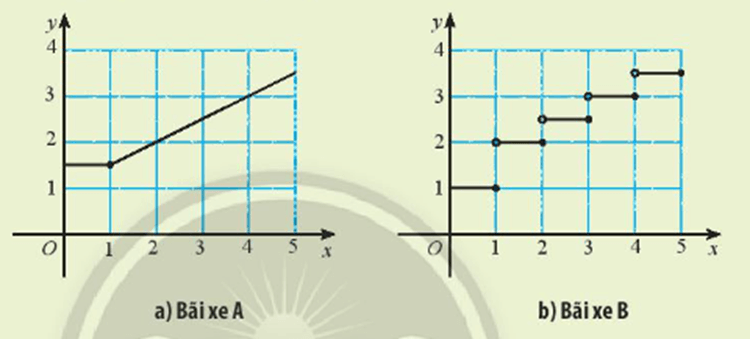
+) Bãi xe A:
Dựa vào đồ thị hàm số ta thấy, theo thời gian gửi x (giờ) tăng thì phí gửi xe tăng dần.
+) Bãi xe B:
Dựa vào đồ thị hàm số ta thấy, theo thời gian gửi x (giờ) tăng thì phí gửi xe tăng dần theo nấc.
1. Hàm số liên tục tại một điểm
Hoạt động khám phá 1 trang 80 Toán 11 Tập 1: Cho hàm số 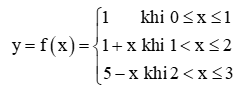
Tại mỗi điểm x0 = 1 và x0 = 2, có tồn tại giới hạn limx→x0f(x) không? Nếu có, giới hạn đó có bằng f(x0) không?
Lời giải:
+) Tại x0 = 1 ta có:
Dãy (xn) bất kì thỏa mãn xn < 1 và xn → 1 thì f(xn) = 1 khi đó limxn→1−f(xn)=1.
Dãy (xn) bất kì thỏa mãn 1 < xn ≤ 2 và xn → 1 thì f(xn) = 1 + xn khi đó limx→1+f(xn)=2.
Suy ra limxn→1−f(xn)≠limxn→1+f(xn). Do đó không tồn tại limx→1f(x).
+) Tại x0 = 2
Dãy (xn) bất kì thỏa mãn xn < 2 và xn → 2 thì f(xn) = 1 + xn khi đó limxn→2−f(xn)=3.
Dãy (xn) bất kì thỏa mãn 2 < xn ≤ 3 và xn → 2 thì f(xn) = 5 – xn khi đó limx→2+f(xn)=3.
Suy ra limxn→2−f(xn)=limxn→2+f(xn)=3. Do đó limx→2f(x)=3.
Ta có f(2) = 1 + 2 = 3.
Vì vậy limx→2f(x)=f(2)=3.
Thực hành 1 trang 81 Toán 11 Tập 1: Xét tính liên tục của hàm số:
a) f(x) = 1 – x2 tại điểm x0 = 3;
b) 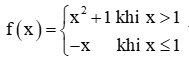
Lời giải:
a) Ta có: limx→3f(x)=limx→3(1−x2)=−8 và f(3) = 1 – 32 = – 8.
Do đó limx→3f(x)=f(3)=−8
Vì vậy hàm số liên tục tại x = 3.
b) Tại x0 = 1:
limx→1+f(x)=limx→1+(x2+1)=2 và limx→1−f(x)=limx→1−(−x)=−1.
Suy ra limx→1+f(x)≠limx→1−f(x)
Do đó không tồn tại limx→1f(x).
Vậy hàm số đã cho không liên tục tại x0 = 1.
2. Hàm số liên tục trên một khoảng, trên một đoạn
Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số 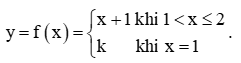
a) Xét tính liên tục của hàm số tại mỗi điểm x0 ∈ (1; 2).
b) Tìm limx→2−f(x) và so sánh giá trị này với f(2).
c) Với giá trị nào của k thì limx→1+f(x)=k?
Lời giải:
a) Tại mỗi điểm x0 ∈ (1; 2) thì f(x) = x + 1
Khi đó: limx→x0f(x)=limx→x0(x+1)=x0+1 và f(x0) = x0 + 1
Suy ra limx→x0f(x)=f(x0)=x0+1
Vì vậy hàm số liên tục tại x0.
b) Tại x0 = 2 ta có f(x) = x + 1, khi đó:
limx→2−f(x)=limx→2−(1+x)=3
f(2) = 2 + 1 = 3
Vậy limx→2−f(x)=f(2)=3.
c) +) Tại x0 = 1 ta có f(x0) = k;
+) Tại x0 = 1
Dãy (xn) bất kì thỏa mãn 1 < xn ≤ 2 và xn → 1 thì f(xn) = xn + 1 khi đó limxn→1+f(xn)=limxn→1+(xn+1)=2.
Suy ra limx→1+f(x)=2
Để limx→1+f(x)=k thì k = 2.
Thực hành 2 trang 82 Toán 11 Tập 1: Xét tính liên tục của hàm số: y=√x−1+√2−x trên [1; 2].
Lời giải:
Đặt y=f(x)=√x−1+√2−x
Với mọi x0 ∈ (1; 2), ta có:
limx→x0f(x)=limx→x0(√x−1+√2−x)=√x0−1+√2−x0=f(x0)
Ta lại có:
limx→1+f(x)=limx→1+(√x−1+√2−x)=1=f(1);
limx→2−f(x)=limx→2−(√x−1+√2−x)=1=f(2).
Vậy hàm số y=√x−1+√2−x liên tục trên [1; 2].
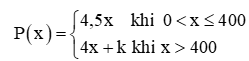
a) Với k = 0, xét tính liên tục của hàm số P(x) trên (0; +∞).
b) Với giá trị nào của k thì hàm số P(x) liên tục trên (0; +∞)?
Lời giải:
a) Với k = 0, hàm số
+) Lấy x0 ∈ (0; 400) khi đó P(x) = 4,5x
Suy ra limx→x0P(x)=limx→x0(4,5x)=4,5x0=P(x0)
Do đó P(x) liên tục trên (0; 400).
+) Tại x0 = 400, ta có:
limx→400−P(x)=limx→400−(4,5x)=4,5.400=1800.
limx→400+P(x)=limx→400+(4x)=4.400=1600.
Suy ra limx→400−P(x)≠limx→400+P(x). Do đó không tồn tại limx→400P(x).
Vì vậy hàm số không liên tục tại x = 400.
+) Lấy x0 ∈ (400; +∞) khi đó P(x) = 4x
Suy ra limx→x0P(x)=limx→x0(4x)=4x0=P(x0)
Do đó P(x) liên tục trên (400; +∞) .
Vậy hàm số liên tục trên (0; 400) và (400; +∞).
b) Để hàm số P(x) liên tục trên (0; +∞) thì P(x) phải liên tục trên x0 = 400.
Do đó limx→400−P(x)=limx→400+P(x)⇔1800=4.400+k⇔k=200.
Vậy với k = 200 thì hàm số liên tục trên (0; +∞).
3. Tính liên tục của hàm số sơ cấp
Hoạt động khám phá 3 trang 82 Toán 11 Tập 1: Cho hai hàm số y = f(x) = 1x−1 và y = g(x) = √4−x.
a) Tìm tập xác định của mỗi hàm số đã cho.
b) Mỗi hàm số liên tục trên những khoảng nào? Giải thích.
Lời giải:
a) +) Xét hàm số: y = f(x) = 1x−1
Điều kiện xác định của hàm số là x ≠ 1.
Vậy tập xác định của hàm số là: D = ℝ \ {1}.
+) Xét hàm số: y = g(x) = √4−x
Điều kiện xác định của hàm số là: 4 – x ≥ 0 ⇔ x ≤ 4.
Vậy tập xác định của hàm số là: D = (– ∞; 4].
b) +) Xét hàm số f(x):
Với x0 ∈ ( – ∞; 1) thì limx→x0f(x)=limx→x011−x=11−x0=f(x0).
Suy ra hàm số f(x) liên tục trên (– ∞; 1).
Với x0 ∈ ( 1; + ∞) thì limx→x0f(x)=limx→x011−x=11−x0=f(x0).
Suy ra hàm số f(x) liên tục trên (1; + ∞).
+) Xét hàm số g(x):
Với x0 ∈ (– ∞; 4) thì limx→x0g(x)=limx→x0√4−x=√4−x0=g(x0).
Tại x0 = 4 thì limx→4−g(x)=limx→4−√4−x=0=g(4).
Vậy hàm số liên tục trên (– ∞; 4].
Thực hành 3 trang 83 Toán 11 Tập 1: Xét tính liên tục của hàm số y=√x2−4.
Lời giải:
Đặt y = f(x) = √x2−4
Tập xác định của hàm số D = (– ∞; 2) ∪ (2; +∞).
Với x0 ∈ ( – ∞; 2) thì limx→x0f(x)=limx→x0√x2−4=√x20−4=f(x0)
Suy ra hàm số liên tục trên ( – ∞; 2).
Với x0 ∈ ( 2; +∞) thì limx→x0f(x)=limx→x0√x2−4=√x20−4=f(x0)
Suy ra hàm số liên tục trên (2; +∞).
Thực hành 4 trang 83 Toán 11 Tập 1: Cho hàm số f(x) = 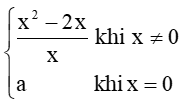
Lời giải:
+) Với x ≠ 0 thì f(x) = x2−2xx liên tục trên (– ∞; 0) và (0; + ∞).
+) Với x = 0 thì
Ta có: limx→0f(x)=limx→0x2−2xx=limx→0x(x−2)x=limx→0(x−2)=−2 và f(0) = a.
Để y = f(x) liên tục trên ℝ thì f(x) phải liên tục tại x = 0 do đó a = – 2.
T(x) =
Xét tính liên tục của hàm số T(x).
Lời giải:
+) Với x0 ∈ (0; 0,7) hàm số f(x) = 10 000 là hàm đa thức nên liên tục trên (0; 0,7).
+) Với x0 ∈ (0,7; 20) hàm số f(x) = 10 000 + (x – 0,7).14 000 là hàm đa thức nên liên tục trên (0,7; 20).
+) Với x0 ∈ (20; +∞) hàm số f(x) = 280 200 + (x – 20).12 000 là hàm đa thức nên liên tục trên (20; +∞).
+) Tại x0 = 0,7 ta có:
limx→0,7−f(x)=limx→0,7−10000=10000;
limx→0,7+f(x)=limx→0,7+[10 000 + (x-0,7).14 000] = 10 000.
Suy ra limx→0,7−f(x)=limx→0,7+f(x)=10000. Do đó tồn tại limx→0,7f(x)=10000.
Mà f(0,7) = 10 000 nên limx→0,7f(x)= f(0,7) = 10000.
Vì vậy hàm số liên tục tại x0 = 0,7.
+) Tại x0 = 20 ta có:
limx→20−f(x)=limx→20−[10 000 + (x-0,7).14 000] = 280 200.
limx→20+f(x)=limx→20+[280 200+(x-20).12 000] = 280 200.
Suy ra limx→20−f(x)=limx→20+f(x)=280200. Do đó tồn tại limx→20f(x)=280200.
Mà f(20) = 280 200 nên limx→20f(x)=f(20)=280200.
Vì vậy hàm số liên tục tại x = 20.
Vậy hàm số T(x) liên tục trên ℝ.
4. Tổng, hiệu, tích, thương của hàm số liên tục
Lời giải:
Xét hàm số y = h(x) = f(x) + g(x) = 1x−1+√4−x có tập xác định D = [4; +∞) \ {1}.
Tại x0 = 2 ∈ D thì limx→2h(x)=limx→2(1x−1+√4−x) = 3 = h(2).
Do đó hàm số liên tục tại x0 = 2.
Thực hành 5 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số:
a) y = √x2+1 + 3 - x;
b) y = x2−1x.cos x.
Lời giải:
a) Đặt y = f(x) = √x2+1 + 3 - x
Tập xác định của hàm số D = ℝ.
Khi đó limx→x0f(x)=limx→x0(√x2+1+3−x)=√x20+1+3−x0=f(x0).
Vậy hàm số liên tục trên ℝ.
b) Đặt y = g(x) = x2−1x.cos x.
Tập xác định của hàm số D = ℝ\{0}.
Trên các khoảng (– ∞; 0) và (0; +∞) ta thấy hàm số y=x2−1x và y = cos x liên tục.
Vậy hàm số đã cho liên tục trại mọi điểm x0 ≠ 0.
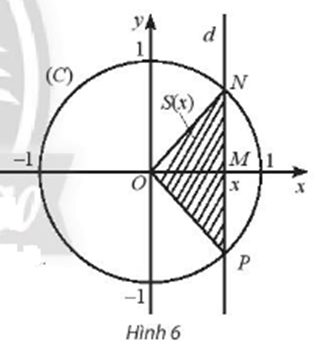
a) Viết biểu thức S(x) biểu thị diện tích của tam giác ONP.
b) Hàm số y = S(x) có liên tục trên (– 1; 1) không? Giải thích.
c) Tìm các giới hạn limx→1−S(x) và limx→−1+S(x).
Lời giải:
a) Xét tam giác OMN vuông tại M có:
MN = √ON2−OM2=√1−x2
⇒NP=2√1−x2
Diện tích của tam giác ONP là:
S(x) = 12.NP.OM = 12.2.√1-x2.x = x√1-x2
b) Trên (– 1; 1) hàm số y = √1-x2 xác định và liên tục và hàm số y = x liên tục.
Do đó hàm số S(x) liên tục trên (– 1; 1).
c) Ta có:
limx→−1+S(x)=limx→−1+(√1−x2.x)=0
limx→1−S(x)=limx→1−(√1−x2.x)=0.
Bài tập
Bài 1 trang 84 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:
a) f(x) = 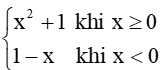
b) f(x) = 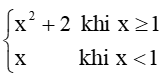
Lời giải:
a) Tại x = 0, ta có:
limx→0+f(x)=limx→0+(x2+1)=1;
limx→0−f(x)=limx→0−(1−x)=1.
Suy ra limx→0+f(x)=limx→0−f(x)=1. Do đó limx→0f(x)=1
Mà f(0) = 02 + 1 = 1 nên limx→0f(x)=f(0)=1.
Vậy hàm số đã cho liên tục tại điểm x = 0.
b) Tại x = 1 ta có:
limx→1+f(x)=limx→1+(x2+2)=3;
limx→1−f(x)=limx→1−x=1.
Suy ra limx→1+f(x)≠limx→1−f(x). Do đó không tồn tại limx→1f(x).
Vậy hàm số không liên tục tại x = 1.
Bài 2 trang 84 Toán 11 Tập 1: Cho hàm số f(x) = 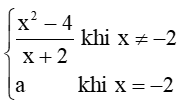
Lời giải:
Ta có:
limx→−2f(x)=limx→−2x2−4x+2=limx→−2(x−2)(x+2)x+2=limx→−2(x−2)=−4.
f(-2) = a.
Để hàm số f(x) liên tục trên ℝ thì hàm số liên tục tại x = – 2
⇔limx→−2f(x)= f(-2)
⇔a = -4
Vậy a = – 4 thì hàm số đã cho liên tục trên ℝ.
Bài 3 trang 85 Toán 11 Tập 1: Xét tính liên tục của hàm số sau:
a) f(x) = xx2−4;
b) g(x) = √9-x2;
c) h(x) = cosx + tanx.
Lời giải:
a) Tập xác định của hàm số D = ℝ \ {– 2; 2}.
Hàm số f(x) = xx2−4 liên tục tại mọi điểm khác – 2 và 2.
b) Tập xác định của hàm số D = [– 2; 2].
Hàm số g(x) = √9-x2 liên tục trên [– 2; 2].
c) Tập xác định của hàm số: D = R\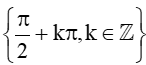
Hàm số y = cosx hoặc y = tanx đều liên tục trên các khoảng xác định của nó.
Vậy h(x) = cosx + tanx liên tục trên từng khoảng xác định.
Lời giải:
+) Xét hàm số y = f(x).g(x) có tập xác định D = [1; +∞).
Hàm số f(x) = 2x – sinx, g(x) = √x−1 đều liên tục trên D.
Vậy hàm số y = f(x).g(x) liên tục trên D.
+) Xét hàm số y = f(x)g(x) có tập xác định D = (1; +∞).
Hàm số f(x) = 2x – sinx, g(x) = √x−1 đều liên tục trên D.
Vậy hàm số y = f(x)g(x) liên tục trên D.
C(x) =
Xét tính liên tục của hàm số C(x).
Lời giải:
+) Với x ∈ (0; 2) ta có: C(x) = 60 000 nên hàm số liên tục trên (0; 2).
+) Với x ∈ (2; 4) ta có: C(x) = 100 000 nên hàm số liên tục trên (2; 4).
+) Với x ∈ (4; 24) ta có: C(x) = 200 000 nên hàm số liên tục trên (4; 24).
+) Tại x = 2 ta có: limx→2−C(x)=60000≠100000=limx→2+C(x). Suy ra không tồn tại limx→2C(x).
+) Tại x = 4 ta có: limx→4−C(x)=100000≠200000=limx→4+C(x). Suy ra không tồn tại limx→4C(x).
Lời giải:
+) Ta có: y = GMrR3 liên tục trên (0; R) và y = GMr2 liên tục trên (R; + ∞).
+) Tại r = R, ta có:
limr→R−F(r)=limr→R−GMrR3=GMR2
limr→R+F(r)=limr→R−GMr2=GMR2
Suy ra limr→R−F(r)=limr→R+F(r). Do đó limr→RF(r)=GMR2
Mà F(R)=GMR2 nên limr→RF(r)=F(R)=GMR2
Suy ra hàm số liên tục tại x = R.
Vậy hàm số liên tục trên (0; +∞).
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian