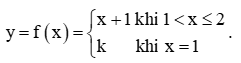Cho hàm số y=f(x). a) Xét tính liên tục của hàm số tại mỗi điểm x0 ∈ (1; 2)

Hoạt động khám phá 2 trang 81 Toán 11 Tập 1: Cho hàm số .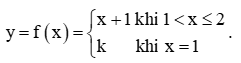

a) Xét tính liên tục của hàm số tại mỗi điểm x₀ ∈ (1; 2).

b) Tìm $\underset{x\to 2^{-}}{\lim }f\left(x\right)$ và so sánh giá trị này với f(2).

c) Với giá trị nào của k thì $\underset{x\to 1^{+}}{\text{lim}}\text{f}\left(x\right)=k$?

Trả lời

a) Tại mỗi điểm x₀ ∈ (1; 2) thì f(x) = x + 1

Khi đó: $\underset{x\to x_0}{\lim }f\left(x\right)=\underset{x\to x_0}{\lim }\left(x+1\right)=x_0+1$ và f(x₀) = x₀ + 1

Suy ra $\underset{x\to x_0}{\lim }f\left(x\right)=f\left(x_0\right)=x_0+1$

Vì vậy hàm số liên tục tại x₀.

b) Tại x₀ = 2 ta có f(x) = x + 1, khi đó:

$\underset{x\to 2^{-}}{\lim }f\left(x\right)=\underset{x\to 2^{-}}{\lim }\left(1+x\right)=3$

f(2) = 2 + 1 = 3

Vậy $\underset{x\to 2^{-}}{\lim }f\left(x\right)=f\left(2\right)=3.$

c) +) Tại x₀ = 1 ta có f(x₀) = k;

+) Tại x₀ = 1

Dãy (x_n) bất kì thỏa mãn 1 < x_n ≤ 2 và x_n → 1 thì f(x_n) = x_n + 1 khi đó $\underset{x_n\to 1^{+}}{\lim }f\left(x_n\right)=\underset{x_n\to 1^{+}}{\lim }\left(x_n+1\right)=2$.

Suy ra $\underset{x\to 1^{+}}{\lim }f\left(x\right)=2$

Để $\underset{x\to 1^{+}}{\lim }f\left(x\right)=k$ thì k = 2.

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Giới hạn của dãy số

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3

Bài 1: Điểm, đường thẳng và mặt phẳng trong không gian

Bài 2: Hai đường thẳng song song