Sách bài tập Toán 8 Bài 34: Ba trường hợp đồng dạng của hai tam giác
(1) 2 cm, 3 cm, 4 cm và 6 cm, 9 cm, 12 cm.
(2) 3 cm, 5 cm, 6 cm và 6 cm, 10 cm, 11 cm.
(3) 2 cm, 3 cm, 3 cm và 2 cm, 2 cm, 3 cm.
(4) 4 cm, 4 cm, 4cm và 3 cm, 3 cm, 3 cm.
Lời giải:
(1) Vì 26=39=412 nên hai tam giác này đồng dạng với nhau theo trường hợp cạnh – cạnh – cạnh.
(2) Vì 36=510≠611 nên hai tam giác này không đồng dạng với nhau.
(3) Vì 22=33≠32 nên hai tam giác này không đồng dạng với nhau.
(4) Vì 43=43=43 nên hai tam giác này đồng dạng với nhau theo trường hợp cạnh – cạnh – cạnh.
Lời giải:
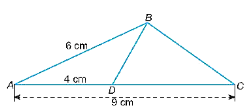
Theo tính chất dãy tỉ số bằng nhau ta có:
34=ABDE=ACDF=AB+ACDE+DF=15−BC20−FE
Do đó,
4(15 – BC) = 3(20 – FE)
60 – 4BC = 60 – 3FE
4BC = 3FE
Suy ra BCFE=34 .
Tam giác ABC và tam giác DEF có:
ABDE=ACDF=BCEF(=34).
Nên ∆ABC ᔕ ∆DEF (c.c.c).
Đề bài của sách bài tập chưa chính xác, cần sửa như sau:
Cho hai tam giác ABC và DEF thỏa mãn 2AB = 3AC = 4BC và DE = 6 cm, DF = 4 cm, EF = 4 cm. Chứng minh rằng ∆ABC ᔕ ∆DEF.
Lời giải:
Vì DE = 6 cm, DF = 4 cm, EF = 3 cm nên ta có: DE : DF : EF = 6 : 4 : 3.
Do đó DE6=DF4=EF3 . Suy ra 2DE12=3DF12=4EF12 .
Suy ra 2DE = 3DF = 4EF.
Mà 2AB = 3AC = 4BC (gt)
Do đó, ABDE=ACDF=BCEF .
Suy ra, ∆ABC ᔕ ∆DEF (c.c.c).
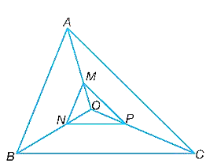
Lời giải:
Vì OA = 3OM, OB = 3ON, OC = 3OP.
Nên OAOM=3;OBON=3;OCOP=3 . Suy ra OAOM=OBON=OCOP=3 .
Tam giác OMN có: OAOM=OBON.
Nên suy ra AB song song với MN (định lí Thalès đảo).
Do đó, ABMN=OAOM=3 .
Chứng minh tương tự ta có: ACMP=3;BCNP=3 .
Tam giác ABC và tam giác MNP có:
ABMN=ACMP=BCNP=3.
Do đó, ∆ABC ᔕ ∆MNP (c.c.c) với tỉ số đồng dạng 3.
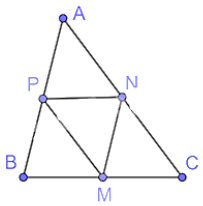
Lời giải:
Tam giác ABC có:
M, N lần lượt là trung điểm của BC, CA
Nên MN là đường trung bình của tam giác ABC.
Do đó, MN // AB và ABMN=2 .
Chứng minh tương tự ta có:BCPN=2; ACPM=2 .
Tam giác ABC và tam giác MNP có:
ABMN=BCPN=ACPM(= 2).
Nên ∆ABC ᔕ ∆MNP (c.c.c) theo tỉ số đồng dạng là 2.
Lời giải:
Tam giác ABD và tam giác BDC có:
ABBD=BDDC=ADBC (do 24=48=36=12
Do đó, ∆ABD ᔕ ∆BDC (c.c.c).
Suy ra: ^ABD=^BDC (hai góc tương ứng).
Mà hai góc này ở vị trí so le trong. Do đó, AB song song với CD.
Lời giải:
Vì tam giác MNP đồng dạng với tam giác ABC nên:
MNAB=NPBC=MPAC(các cạnh tương ứng tỉ lệ).
Mà trong tam giác ABC, cạnh AC lớn nhất nên trong tam giác MNP cạnh lớn nhất là MP.
Do đó, MP = 9 cm.
Khi đó MNAB=NPBC=MPAC=96=32 .
Suy ra: MN=32AB=32.4=6 (cm), NP=32BC=32⋅5=152 (cm).
(1) ∆ABC ᔕ ∆DEF.
(2) ∆CAB ᔕ ∆DEF.
(3) ∆ABC ᔕ ∆EFD
(4) ∆BCA ᔕ ∆EFD.
(5) ∆ABC ᔕ ∆FDE.
(6) ∆BAC ᔕ ∆FED.
Lời giải:
Hai tam giác ABC và tam giác DEF có:
ABEF=BCDF
^ABC=^DFE
Do đó, ∆ABC ᔕ ∆EFD (c.g.c).
Khi đó, đỉnh A tương ứng với đỉnh E, đỉnh B tương ứng với đỉnh F và đỉnh C tương ứng với đỉnh D.
Suy ra các đáp án đúng là (2), (3), (6).
(1) ∆ABC ᔕ ∆MNP.
(2) ∆BCA ᔕ ∆MNP.
(3) ∆ABC ᔕ ∆NPM.
(4) ∆CAB ᔕ ∆NPM.
(5) ∆ABC ᔕ ∆PMN.
(6) ∆BAC ᔕ ∆MNP.
Lời giải:
Tam giác ABC và tam giác MNP có:
^ABC=^NMP
^ACB=^MNP
Do đó, ∆ABC ᔕ ∆PMN (g.g).
Khi đó đỉnh A tương ứng với đỉnh P, đỉnh B tương ứng với đỉnh M, đỉnh C tương ứng với đỉnh N.
Suy ra, các khẳng định đúng là (2), (4), (5).
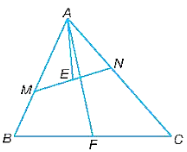
a) Chứng minh rằng ∆AMN ᔕ ∆ACB.
b) Lấy E, F lần lượt là trung điểm của MN, BC. Chứng minh rằng ^EAB=^FAC .
Lời giải:
Vì AM . AB = AN . AC nên AMAC=ANAB .
Tam giác AMN và tam giác ABC có:
AMAC=ANAB
^BAC chung.
Do đó, ∆AMN ᔕ ∆ACB (c.g.c).
b)
Vì ∆AMN ᔕ ∆ACB (cmt) nên ^AMN=ˆC và AMAC=MNCB .
Mà E, F lần lượt là trung điểm của MN, BC nên MN = 2ME, BC = 2FC.
Do đó: AMAC=MNCB=2ME2FC=MEFC .
Tam giác MAE và tam giác CAF có:
^AME=ˆC (do ^AMN=ˆC );
AMAC=MEFC(cmt).
Do đó, ∆AME ᔕ ∆ACF (c.g.c). Suy ra ^EAM=^FAC (hai góc tương ứng).
Vậy ^EAB=^FAC .
a) AP . AB = AQ . AC.
b) ∆APC ᔕ ∆AQB.
Lời giải:
a)
Xét tam giác APQ và tam giác ACB có:
^PAQ=^BAC (hai góc đối đỉnh)
^APQ=^ACB (giả thiết)
Do đó, ∆APQ ᔕ ∆ACB (g.g) nên APAC=AQAB .
Suy ra: AP . AB = AQ . AC.
b)
Vì APAC=AQAB nên APAQ=ACAB.
Xét tam giác APC và tam giác AQB có:
^PAC=^BAQ (hai góc đối đỉnh),
APAQ=ACAB (chứng minh trên).
Do đó, ∆APC ᔕ ∆AQB (c.g.c).
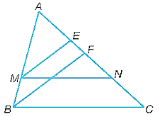
a) ∆MEN ᔕ ∆BFC.
b) AEAF=MNBC .
Lời giải:
a)
Vì MN song song với BC (gt) nên
^ENM=ˆC (hai góc đồng vị);
^AMN=^ABC (hai góc đồng vị).
Mà ME, BF lần lượt là phân giác của các góc M, B của các tam giác AMN và tam giác ABC nên ^EMN=12^AMN và ^FBC=12^ABC. Do đó, ^EMN=^FBC.
Tam giác MEN và tam giác BFC có:
^ENM=ˆC (cmt)
^EMN=^FBC (cmt)
Do đó, tam giác MEN đồng dạng với tam giác BFC (g.g).
b)
Tam giác ABC có:
MN song song với BC
Nên theo hệ quả định lý Thalès ta có:
MNBC=AMAB(1).
Vì ME, BF lần lượt là phân giác của ˆM , ˆB của tam giác AMN và tam giác ABC nên ^EMA=12^AMN=12^ABC=^FBA .
Do đó ^EMA=^FBA , mà hai góc này ở vị trí đồng vị nên ME song song với BF.
Tam giác ABF có ME song song với BF nên theo hệ quả định lý Thalès ta có:
AEAF=AMAB (2).
Từ (1) và (2) ta có: AEAF=MNBC .
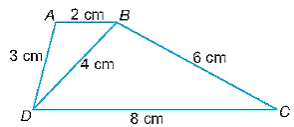
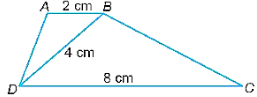
Lời giải:
Vì AB song song CD nên ^ABD=^BDC (hai góc so le trong).
Tam giác ABD và tam giác BDC có:
ABBD=BDDC (do 24=48=12 )
^ABD=^BDC(cmt)
Do đó, ∆ABD ᔕ ∆BDC (c.g.c).
Suy ra: BDDC=ADBC=ABBD=12 .
Do đó, BC = 2AD.
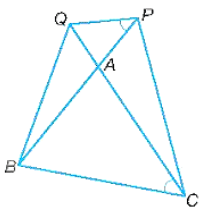
a) Chứng minh rằng: ∆EAB ᔕ ∆EDC, ∆FAB ᔕ ∆FCD.
b) Lấy hai điểm M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, E, F thẳng hàng.
Lời giải:
a)
Vì AB song song với đáy CD của tam giác EDC nên ∆EAB ᔕ ∆EDC.
Vì AB song song với đáy CD của tam giác FCD nên ∆FAB ᔕ ∆FCD.
b)
Vì ∆EAB ᔕ ∆EDC (cmt) nên EAED=ABDC=2AM2DN=AMDN (do M, N lần lượt là trung điểm của AB, CD).
Tam giác EAM và tam giác EDN có:
EAED=AMDN (cmt)
^EAM=^EDN (AM song song với DN, hai góc đồng vị)
Do đó, ∆EAM ᔕ ∆EDN (c.g.c).
Suy ra ^AEM=^DEN.
Do đó, tia EM trùng với tia EN hay 3 điểm M, E, N thẳng hàng (1).
Vì ∆FAB ᔕ ∆FCD nên FAFC=ABCD=AMCN .
Hai tam giác FAM và tam giác FCN có:
FAFC=AMCN (cmt)
^FAM=^FCN (AM song song với CN, hai góc so le trong)
Do đó, ∆FAM ᔕ ∆FCN (c.g.c).
Nên ^AFM=^CFN
Do đó, tia FM và tia FN là hai tia đối nhau.
Suy ra, F, M, N thẳng hàng (2).
Từ (1) và (2) ta có: 4 điểm M, E, F, N thẳng hàng.
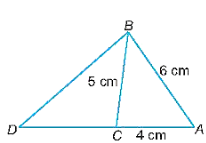
Lời giải:
Xét hai tam giác ABD và tam giác ACB có:
ˆA chung
ABAC=ADAB (do 69=46=23 )
Do đó, ∆ABD ᔕ ∆ACB (c.g.c).
Suy ra BDBC=ABAC=69=23 .
Nên BC = 32 BD.
Lời giải:
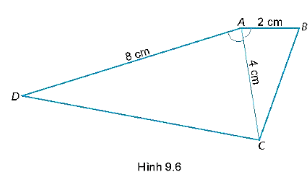
Xét tam giác ABC và tam giác ACD có:
^BAC=^DAC (vì AC là tia phân giác của )
ABAC=ACAD (do 24=48 )
Suy ra ∆ABC ᔕ ∆ACD (c.g.c).
Do đó, BCCD=ABAC=24=12 .
Suy ra CD = 2BC.
Lời giải:
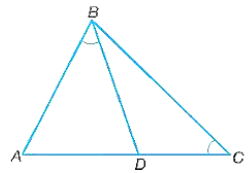
Xét tam giác ABD và tam giác ACB có:
ˆA chung
^ABD=^BCA (gt)
Do đó, ∆ABD ᔕ ∆ACB (g.g).
Suy ra ADAB=ABAC .
Nên AB2 = AD . AC.
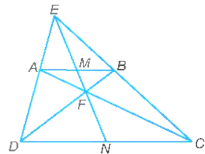
a) AM . AB = AN . AC.
b) OM . OC = ON . OB.
Lời giải:
a)
Xét tam giác ABN và tam giác ACM có:
ˆA chung
^ABN=^ACM (gt)
Do đó, ∆ABN ᔕ ∆ACM (g.g).
Suy ra ABAC=ANAM nên AM . AB = AN . AC.
b)
Tam giác BOM và tam giác CON có:
^MBO=^NCO (do ^ABN=^ACM )
^MOB=^NOC (hai góc đối đỉnh)
Nên ∆BOM ᔕ ∆CON (g.g).
Suy ra OMON=OBOC nên OM . OC = ON . OB.
a) ∆ABC ᔕ ∆ADB.
b) ^ACB=2^ABC .
Lời giải:
a)
Ta có: AD = AC + DC = AC + BC = 4 + 5 = 9 (cm).
Xét tam giác ABC và tam giác ADB có:
ˆA chung
ABAD=ACAB (69=46).
Do đó, ∆ABC ᔕ ∆ADB (c.g.c).
b)
Vì ∆ABC ᔕ ∆ADB (cmt) nên ^ABC=^ADB .
Mà tam giác BCD cân tại C (do CD = CB) nên ^CBD=^BDC hay ^CBD=^ADB .
Do đó, ^CBD=^ABC .
Vì góc ACB là góc ngoài tại đỉnh C của tam giác DBC nên ta có:
^ACB=^CDB+^CBD=2^CBD=2^ABC.
Vậy ^ACB=2^ABC .
Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: