Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho AM . AB = AN . AC

Bài 9.21 trang 56 SBT Toán lớp 8 Tập 2: Cho hai điểm M, N lần lượt nằm trên hai cạnh AB, AC của tam giác ABC sao cho AM . AB = AN . AC.

a) Chứng minh rằng ∆AMN ᔕ ∆ACB.

b) Lấy E, F lần lượt là trung điểm của MN, BC. Chứng minh rằng $\widehat{EAB}=\widehat{FAC}$ .

Trả lời

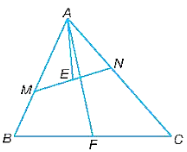
Vì AM . AB = AN . AC nên $\frac{AM}{AC}=\frac{AN}{AB}$ .

Tam giác AMN và tam giác ABC có:

$\frac{AM}{AC}=\frac{AN}{AB}$

$\widehat{BAC}$ chung.

Do đó, ∆AMN ᔕ ∆ACB (c.g.c).

b)

Vì ∆AMN ᔕ ∆ACB (cmt) nên $\widehat{AMN}=\widehat{C}$  và $\frac{AM}{AC}=\frac{MN}{CB}$ .

Mà E, F lần lượt là trung điểm của MN, BC nên MN = 2ME, BC = 2FC.

Do đó: $\frac{AM}{AC}=\frac{MN}{CB}=\frac{2ME}{2FC}=\frac{ME}{FC}$ .

Tam giác MAE và tam giác CAF có:

$\widehat{AME}=\widehat{C}$ (do $\widehat{AMN}=\widehat{C}$ );

$\frac{AM}{AC}=\frac{ME}{FC}$(cmt).

Do đó, ∆AME ᔕ ∆ACF (c.g.c). Suy ra $\widehat{EAM}=\widehat{FAC}$ (hai góc tương ứng).

Vậy $\widehat{EAB}=\widehat{FAC}$ .

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: