Cho tam giác ABC với AB = 6 cm, AC = 4 cm, BC = 5 cm. Trên tia đối của tia CA lấy điểm D sao cho CD = CB

Bài 9.30 trang 57 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB = 6 cm, AC = 4 cm, BC = 5 cm. Trên tia đối của tia CA lấy điểm D sao cho CD = CB. Chứng minh rằng:

a) ∆ABC ᔕ ∆ADB.

b) $\widehat{ACB}=2\widehat{ABC}$ .

Trả lời

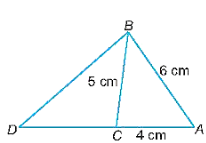
a)

Ta có: AD = AC + DC = AC + BC = 4 + 5 = 9 (cm).

Xét tam giác ABC và tam giác ADB có:

$\widehat{A}$ chung

$\frac{AB}{AD}=\frac{AC}{AB}\left(\frac{6}{9}=\frac{4}{6}\right)$.

Do đó, ∆ABC ᔕ ∆ADB (c.g.c).

b)

Vì ∆ABC ᔕ ∆ADB (cmt) nên $\widehat{ABC}=\widehat{ADB}$ .

Mà tam giác BCD cân tại C (do CD = CB) nên $\widehat{CBD}=\widehat{BDC}$  hay $\widehat{CBD}=\widehat{ADB}$  .

Do đó, $\widehat{CBD}=\widehat{ABC}$ .

Vì góc ACB là góc ngoài tại đỉnh C của tam giác DBC nên ta có:

$\widehat{ACB}=\widehat{CDB}+\widehat{CBD}=2\widehat{CBD}=2\widehat{ABC}$.

Vậy $\widehat{ACB}=2\widehat{ABC}$ .

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: