Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho góc APQ = góc ACB. Chứng minh rằng

Bài 9.22 trang 56 SBT Toán lớp 8 Tập 2: Cho tam giác ABC và hai điểm P, Q lần lượt nằm trên các tia đối của tia AB và AC sao cho $\widehat{APQ}=\widehat{ACB}$  . Chứng minh rằng:

a) AP . AB = AQ . AC.

b) ∆APC ᔕ ∆AQB.

Trả lời

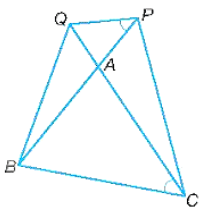
a)

Xét tam giác APQ và tam giác ACB có:

 $\widehat{PAQ}=\widehat{BAC}$ (hai góc đối đỉnh)

 $\widehat{APQ}=\widehat{ACB}$ (giả thiết)

Do đó, ∆APQ ᔕ ∆ACB (g.g) nên $\frac{AP}{AC}=\frac{AQ}{AB}$ .

Suy ra: AP . AB = AQ . AC.

b)

Vì  $\frac{AP}{AC}=\frac{AQ}{AB}$ nên $\frac{AP}{AQ}=\frac{AC}{AB}$.

Xét tam giác APC và tam giác AQB có:

$\widehat{PAC}=\widehat{BAQ}$ (hai góc đối đỉnh),

$\frac{AP}{AQ}=\frac{AC}{AB}$ (chứng minh trên).

Do đó, ∆APC ᔕ ∆AQB (c.g.c).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: