Giải SBT Toán 8 (Kết nối tri thức) Bài 35: Định lí Pythagore và ứng dụng

Sách bài tập Toán 8 Bài 35: Định lí Pythagore và ứng dụng

Bài 9.31 trang 59 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại A. Khẳng định nào sau đây là đúng ?

(1) AB² + BC² = AC².

(2) AB + BC = AC.

(3) AB² + AC² = BC².

(4) AB + AC = BC.

(5) AC² + BC² = AB².

(6) AC + BC = AB.

Lời giải:

Vì tam giác ABC vuông tại A nên:

BC là cạnh huyền

Hai cạnh góc vuông là AB, AC.

Theo định lý Pythagore ta có:

BC² = AB² + AC²

Vậy khẳng đúng là khẳng định (3).

Bài 9.32 trang 59 SBT Toán lớp 8 Tập 2: Những bộ ba số đo nào dưới đây là độ dài ba cạnh của một tam giác vuông?

(1) 1 cm, 1 cm, 2 cm.

(2) 1 cm, 1 cm, $\sqrt{2}$  cm.

(3) 2 cm, 4 cm, 20 cm.

(4) 2 cm, 4 cm, $\sqrt{20}$  cm.

(5) 3 cm, 4 cm, 5 cm.

(6) 9 cm, 16 cm, 25 cm.

Lời giải:

(1) Vì 1² + 2² ≠ 2² nên bộ ba số đo 1 cm, 1 cm, 2 cm không là độ dài ba cạnh của một tam giác vuông.

(2) Vì 1² + 1² =  ${\left(\sqrt{2}\right)}^2$ nên bộ ba số đo 1 cm, 1 cm, $\sqrt{2}$cm là độ dài ba cạnh của một tam giác vuông.

(3) Vì 2² + 4² ≠ 20² nên bộ ba số đo 2 cm, 4 cm, 20 cm không là độ dài ba cạnh của một tam giác vuông

(4) Vì 2² + 4² =  ${\left(\sqrt{20}\right)}^2$ nên bộ ba số đo 2 cm, 4 cm,  $\sqrt{20}$ cm là độ dài ba cạnh của một tam giác vuông.

(5) Vì 3² + 4² = 5² (= 25) nên bộ ba số đo 3 cm, 4 cm, 5 cm là độ dài ba cạnh của một tam giác vuông.

(6) Vì 9² + 16² ≠ 25² nên bộ ba số đo 9 cm, 16 cm, 25 cm không là độ dài ba cạnh của một tam giác vuông.

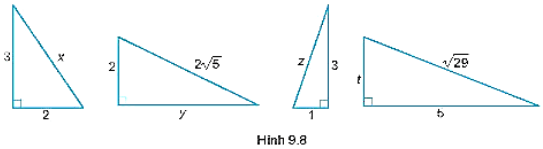
Bài 9.33 trang 59 SBT Toán lớp 8 Tập 2: Tính các độ dài x, y, z, t trong Hình 9.8

Lời giải:

Áp dụng định lý Pythagore vào các tam giác vuông trong Hình 9.8, ta có:

+) x² = 3² + 2² = 9 + 4 = $\sqrt{13}$ nên x =  (đvđd).

+) 2² + y² = ${\left(2\sqrt{5}\right)}^2$  nên y² = 20 – 4 = 16, suy ra y = 4 (đvđd).

+) z² = 3² + 1² = 9 + 1 = 10 nên z = $\sqrt{10}$  (đvđd).

+) t² + 5² = ${\left(\sqrt{29}\right)}^2$  nên t² = 29 – 25 = 4 nên t = 2 (đvđd).

Bài 9.34 trang 59 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông cân tại đỉnh A có đường cao AH. Biết rằng AB = 4 cm, hãy tính độ dài cạnh đáy BC và chiều cao AH.

Lời giải:

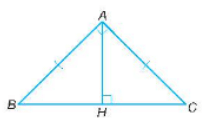
Vì tam giác ABC vuông cân tại A nên

AC = AB = 4 cm

$\widehat{B}=\widehat{C}=45°$

Tam giác AHB vuông tại H có $\widehat{B}=45°$ , suy ra tam giác AHB vuông cân tại H.

Nên AH = HB.

Tam giác AHC vuông tại H có $\widehat{C}=45°$  , suy ra tam giác AHC vuông cân tại H.

Nên AH = HC.

Khi đó, HB = HC = AH.

Mà HB + HC = BC. Suy ra HB + HB = BC hay 2HB = BC.

Do đó, AH = HC = HB = $\frac{1}{2}$ BC.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A ta có:

BC² = AB² + AC² = 4² + 4² = 32.

Suy ra BC = $\sqrt{32}$  = $4\sqrt{2}$  (cm).

Do đó, AH = $\frac{1}{2}$ BC = $2\sqrt{2}$   (cm).

Bài 9.35 trang 60 SBT Toán lớp 8 Tập 2: Hãy tính độ dài các cạnh của một hình thoi với hai đường chéo lần lượt có độ dài bằng 6 cm và 8 cm

Lời giải:

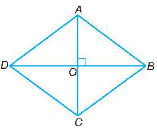
Giả sử hình thoi ABCD có hai đường chéo AC = 6 cm, BD = 8 cm và O là giao điểm của AC và BD. Khi đó, O là trung điểm của AC, O là trung điểm của BD và AC vuông góc với BD tại O.

Suy ra OC = $\frac{1}{2}$ AC = 3 cm, OD =$\frac{1}{2}$ BD = 4 cm và $\widehat{COD}=90°$ .

Do đó, tam giác COD vuông tại O.

Áp dụng định lí Pythagore ta có:

CD² = OC² + OD² = 3² + 4² = 25.

Suy ra CD = 5 cm. Vậy độ dài cạnh của hình thoi là 5 cm.

Bài 9.36 trang 60 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại đỉnh A, có BC = 26 cm và $\frac{AB}{AC}=\frac{5}{12}$. Tính độ dài các cạnh AB, AC.

Lời giải:

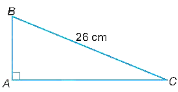
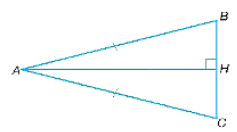
Xét tam giác ABC vuông tại A.

Áp dụng định lí Pythagore ta có:

AB² + AC² = BC² (1)

Mà $\frac{AB}{AC}=\frac{5}{12}$ nên AB = $\frac{5}{12}$ AC, thay vào (1) ta có:

$A{C}^2+{\left(\frac{5}{12}AC\right)}^2={26}^2$

$\frac{169}{144}A{C}^2=676$

AC² = 576

Suy ra AC = 24 cm.

Do đó, AB = $\frac{5}{12}$ .24 = 10 (cm).

Bài 9.37 trang 60 SBT Toán lớp 8 Tập 2: Cho tam giác ABC vuông tại đỉnh A. Gọi AD là đường cao của tam giác. Biết rằng BD = 2 cm, CD = 8 cm. Hãy tính độ dài các cạnh AB, AC và chiều cao AD của tam giác ABC.

Lời giải:

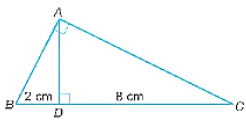
Vì AD là đường cao của tam giác ABC nên AD vuông góc với BC.

Do đó, $\widehat{ADB}=\widehat{ADC}=90°$  .

Tam giác ABD và tam giác CAD có:

$\widehat{ADB}=\widehat{ADC}=90°$ (cmt)

 $\widehat{BAD}=\widehat{C}$ (cùng phụ với góc DAC).

Do đó, ∆ABD ᔕ ∆CAD (g.g).

Suy ra $\frac{AD}{CD}=\frac{BD}{AD}$  nên AD² = CD . BD = 8 . 2 = 16.

Do đó, AD = 4 cm.

Áp dụng định lý Pythagore trong tam giác vuông ABD vuông tại D có:

AB² = AD² + BD² = 4² + 2² = 20.

Nên AB = $2\sqrt{5}$ cm.

Áp dụng định lý Pythagore vào tam giác ACD vuông tại D có:

AC² = AD² + CD² = 4² + 8² = 80.

Nên AC = $4\sqrt{5}$  cm.

Bài 9.38 trang 60 SBT Toán lớp 8 Tập 2: Tìm độ dài cạnh huyền của một tam giác vuông biết rằng tỉ số của độ dài hai cạnh góc vuông là 3 : 4 và chu vi tam giác bằng 48cm.

Lời giải:

Giả sử tam giác ABC vuông tại A có: AB : AC = 3 : 4 và chu vi tam giác bằng 48 cm.

Vì AB : AC = 3 : 4 nên AB =$\frac{3}{4}$ AC.

Áp dụng định lý Pythagore vào tam giác ABC vuông tại A có:

BC² = AB² + AC² =${\left(\frac{3}{4}AC\right)}^2+A{C}^2=\frac{25}{16}A{C}^2$

Nên BC = $\frac{5}{4}AC$ .

Chu vi tam giác ABC là:

AB + BC + AC = 48

$AC+\frac{3}{4}AC+\frac{5}{4}AC=48$

3AC = 48

AC = 16 (cm)

Do đó, BC = $\frac{5}{4}AC$  = $\frac{5}{4}.16$  = 20 (cm).

Bài 9.39 trang 60 SBT Toán lớp 8 Tập 2: Tính diện tích của một tam giác cân, biết rằng tam giác đó có hai cạnh với độ dài bằng 4 cm và 8 cm.

Lời giải:

Vì tam giác cân có hai cạnh là 4 cm và 8 cm nên độ dài cạnh thứ ba của tam giác sẽ là 4 cm hoặc 8 cm.

Mà 4 + 4 = 8 không thỏa mãn bất đẳng thức tam giác nên ta loại trường hợp độ dài ba cạnh là 4 cm, 4 cm, 8 cm.

Do đó, độ dài ba cạnh của tam giác đó là 4 cm, 8 cm, 8 cm.

Giả sử tam giác ABC cân tại A có AB = AC = 8 cm, BC = 4 cm.

Kẻ đường cao AH (H thuộc BC) của tam giác ABC cân tại A. Khi đó, H là trung điểm của BC nên $BH=\frac{1}{2}BC$ = 2 cm.

Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có:

AH² + BH² = AB²

Suy ra AH² = AB² – BH² = 8² – 2² = 60.

Do đó, AH = $2\sqrt{15}$  cm.

Diện tích tam giác ABC là: $\frac{1}{2}AH\cdot BC=\frac{1}{2}\cdot 2\sqrt{15}\cdot 4=4\sqrt{15}$   (cm²).

Bài 9.40 trang 60 SBT Toán lớp 8 Tập 2: Tính chiều cao và diện tích của một tam giác đều có cạnh bằng 4 cm.

Lời giải:

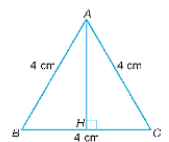
Xét tam giác đều ABC có cạnh AB = AC = BC = 4 cm.

Kẻ đường cao AH của tam giác đều ABC.

Khi đó, đường cao AH đồng thời là đường trung tuyến. Do đó, ta có:

BH = $\frac{1}{2}$ BC = $\frac{1}{2}.4$ = 2 (cm).

Áp dụng định lý Pythagore vào tam giác ABH vuông tại H có:

AH² + BH² = AB²

Suy ra AH² = AB² – BH² = 4² – 2² = 12.

Do đó, $AH=\sqrt{12}$  =$2\sqrt{3}$  (cm).

Diện tích tam giác ABC là: $\frac{1}{2}AH\cdot BC=\frac{1}{2}\cdot 2\sqrt{3}\cdot 4=4\sqrt{3}$ (cm²).

Bài 9.41 trang 60 SBT Toán lớp 8 Tập 2: Một chiếc ti vi màn hình phẳng 32 inch với chiều ngang màn hình là 72 cm (1 inch = 2,54 cm). Tính chiều cao của màn hình ti vi đó.

Lời giải:

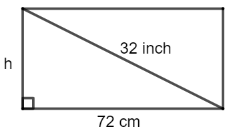
Gọi chiều cao màn hình ti vi là h (cm).

Áp dụng định lý Pythagore cho tam giác vuông với hai cạnh góc vuông là hai cạnh của màn hình chiếc ti vi.

Khi đó, cạnh huyền của tam giác vuông này có độ dài bằng: 32 . 2,54 = 81,28 (cm).

Áp dụng định lý Pythagore cho tam giác vuông ta suy ra:

h² = 81,28² – 72² = 1 422,4384

Suy ra h = $\sqrt{1422,4384}$   ≈ 37,72 (cm).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Bài 33: Hai tam giác đồng dạng

Bài 34: Ba trường hợp đồng dạng của hai tam giác

Bài 36: Các trường hợp đồng dạng của hai tam giác vuông

Bài 37: Hình đồng dạng

Bài tập cuối chương 9