Sách bài tập Toán 8 Bài 33: Hai tam giác đồng dạng
Lời giải:
Khi viết ∆ABC ᔕ ∆MNP thì góc ABC của tam giác CBA tương ứng với góc PNM của tam giác MNP.
Ta có:
Các cặp góc tương ứng bằng nhau: ;
Các cặp cạnh tương ứng tỉ lệ: .
Bài 9.2 trang 52 sách bài tập Toán 8 Tập 2: Cho ∆ABC ᔕ ∆DEF. Những cách viết nào dưới đây đúng ?
(1) ∆BCA ᔕ ∆FED.
(2) ∆CAB ᔕ ∆EDF.
(3) ∆BAC ᔕ ∆EDF.
(4) ∆CBA ᔕ ∆FED.
Lời giải:
Vì ∆ABC ᔕ ∆DEF nên ;
Do đó, đáp án (3), (4) đúng vì:
(3) ∆BAC ᔕ ∆EDF
(4) ∆CBA ᔕ ∆FED
đều suy ra: ;
(1) AB = MN, AC = MP, BC = NP.
(2) .
(3)
(4) .
Lời giải:
Vì ∆ABC ᔕ ∆MNP nên
và .
Do đó, đáp án đúng là (2), (3).
Lời giải:
Vì ∆ABC ᔕ ∆A'B'C' nên , , .
Tam giác ABC có: (tổng ba góc trong một tam giác) nên:
.
Do đó, .
Lời giải:
Vì ∆ABC ᔕ ∆MNP nên: .
Theo tính chất của dãy tỉ số bằng nhau ta có:
.Chu vi tam giác ABC bằng 20 cm nên AB + BC + AC = 20.
Do đó, MN + MP + NP = 20 : = 32 (cm).
Vậy ∆ABC ᔕ ∆MNP với tỉ số đồng dạng và chu vi tam giác MNP bằng 32 cm.
Lời giải:
Theo giả thiết ta có: .
Vì tổng các góc trong một tam giác bằng 180° nên > và .Do hai tam giác đồng dạng thì có các đỉnh tương ứng bằng nhau nên chỉ có thể xảy ra , , kết hợp với . Suy ra ∆ABC ᔕ ∆FDE.
Lời giải:
Vì nên cạnh AB tương ứng với cạnh NP, cạnh AC tương ứng với cạnh PM, cạnh BC tương ứng với cạnh MN.
Do các đỉnh tương ứng sẽ đối diện với các cạnh tương ứng nên các cặp đỉnh tương ứng của hai tam giác đồng dạng đã cho là: C và M, B và N, A và P.
Do đó, ∆ABC ᔕ ∆PNM.
Lời giải:
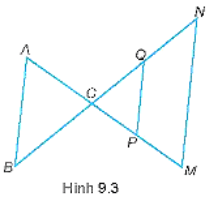
Do PQ song song với AB nên ∆CPQ ᔕ ∆CAB.
Do AB song song với MN nên ∆CMN ᔕ ∆CAB.
Do PQ song song với MN (vì PQ và MN cùng song song với AB) nên ∆CPQ ᔕ ∆CMN.
Lời giải:
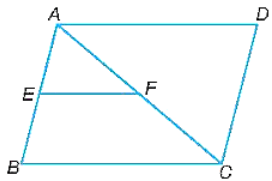
Vì ABCD là hình bình hành nên , AB = CD, BC = AD.
Do đó, ∆ABC = ∆CDA (c.g.c). Suy ra ∆ABC ᔕ ∆CDA (1).
Tam giác ABC có E, F lần lượt là trung điểm của AB và AC nên EF là đường trung bình tam giác ABC. Do đó, EF // BC.
Tam giác ABC có:
EF // BC nên ∆AEF ᔕ ∆ABC (2).
Từ (1) và (2) suy ra: ∆AEF ᔕ ∆CDA
Lời giải:
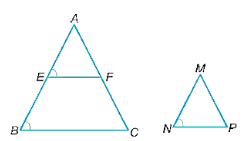
Gọi E, F lần lượt là trung điểm của AB, AC.
Khi đó, EF là đường trung bình của tam giác ABC. Suy ra EF song song với BC.
Do đó, ∆AEF ᔕ ∆ABC.
Lại có : nên ∆ABC ᔕ ∆AEF với tỉ số đồng dạng bằng 2 (1).
Vì EF song song với BC nên : (hai góc đồng vị).
Mà tam giác ABC cân tại A nên .
Do đó, .
Tam giác MNP cân tại M nên .
Lại có: (giả thiết).
Do đó, .
Ta có EF = (do EF là đường trung bình của tam giác ABC) và
(do BC = 2NP). Do đó, EF = NP.
Tam giác AEF và tam giác MNP có:
(chứng minh trên)
EF = NP (chứng minh trên)
Do đó, tam giác AEF và tam giác MNP bằng nhau (g.c.g).
Suy ra ∆AEF ᔕ ∆MNP với tỉ số đồng dạng bằng 1 (2).
Từ (1) và (2) ta có: ∆ABC ᔕ ∆MNP với tỉ số đồng dạng bằng 2.
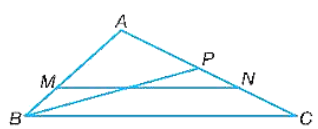
Bài 9.11 trang 52 SBT Toán lớp 8 Tập 2: Cho tam giác ABC với AB = 6 cm, AC = 9 cm.
a) Lấy điểm M, N lần lượt trên các cạnh AB, AC sao cho AM = 4 cm, AN = 6 cm. Chứng minh rằng ∆AMN ᔕ ∆ABC và tìm tỉ số đồng dạng.
b) Lấy điểm P trên cạnh AC sao cho AP = 4 cm. Chứng minh rằng ∆APB ᔕ ∆ABC.
Lời giải:
a) Xét tam giác ABC có:
Suy ra MN song song với BC (định lí Thalès đảo)
Do ∆AMN ᔕ ∆ABC với tỉ số đồng dạng (1).
b) Tam giác APB và tam giác AMN có:
AP = AM (= 4 cm)
chung
AB = AN (= 6 cm)
Do đó, ∆APB = ∆AMN (c.g.c). Suy ra ∆APB ᔕ ∆AMN (2).
Từ (1) và (2) ta có: ∆APB ᔕ ∆ABC
Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác:
