ho hình thang ABCD (AB // CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F

Bài 9.25 trang 56 SBT Toán lớp 8 Tập 2: Cho hình thang ABCD (AB // CD). Biết rằng AD cắt BC tại E, AC cắt BD tại F.

a) Chứng minh rằng: ∆EAB ᔕ ∆EDC, ∆FAB ᔕ ∆FCD.

b) Lấy hai điểm M, N lần lượt là trung điểm của AB, CD. Chứng minh rằng bốn điểm M, N, E, F thẳng hàng.

Trả lời

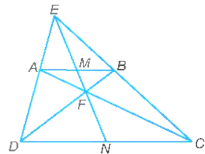
a)

Vì AB song song với đáy CD của tam giác EDC nên ∆EAB ᔕ ∆EDC.

Vì AB song song với đáy CD của tam giác FCD nên ∆FAB ᔕ ∆FCD.

b)

Vì ∆EAB ᔕ ∆EDC (cmt) nên $\frac{EA}{ED}=\frac{AB}{DC}=\frac{2AM}{2DN}=\frac{AM}{DN}$  (do M, N lần lượt là trung điểm của AB, CD).

Tam giác EAM và tam giác EDN có:

 $\frac{EA}{ED}=\frac{AM}{DN}$ (cmt)

$\widehat{EAM}=\widehat{EDN}$ (AM song song với DN, hai góc đồng vị)

Do đó, ∆EAM ᔕ ∆EDN (c.g.c).

Suy ra $\widehat{AEM}=\widehat{DEN}$.

Do đó, tia EM trùng với tia EN hay 3 điểm M, E, N thẳng hàng (1).

Vì ∆FAB ᔕ ∆FCD nên $\frac{FA}{FC}=\frac{AB}{CD}=\frac{AM}{CN}$  .

Hai tam giác FAM và tam giác FCN có:

$\frac{FA}{FC}=\frac{AM}{CN}$ (cmt)

$\widehat{FAM}=\widehat{FCN}$ (AM song song với CN, hai góc so le trong)

Do đó, ∆FAM ᔕ ∆FCN (c.g.c).

Nên $\widehat{AFM}=\widehat{CFN}$

Do đó, tia FM và tia FN là hai tia đối nhau.

Suy ra, F, M, N thẳng hàng (2).

Từ (1) và (2) ta có: 4 điểm M, E, F, N thẳng hàng.

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: