Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A1A2 = 768 800 km và B1B2 = 767 619 km

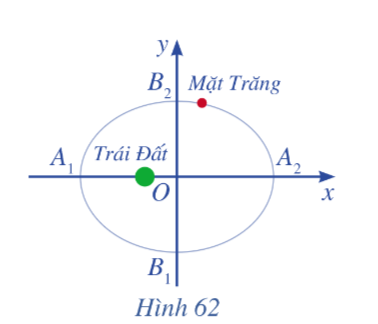
Bài 4 trang 102 Toán 10 Tập 2: Ta biết rằng Mặt Trăng chuyển động quanh Trái Đất theo quỹ đạo là một elip mà Trái Đất là một tiêu điểm. Elip đó có A₁A₂ = 768 800 km và B₁B₂ = 767 619 km (Nguồn: Ron Larson (2014), Precalculus Real Mathematics, Real People, Cengage) (Hình 62). Viết phương trình chính tắc của elip đó.

Trả lời

Phương trình chính tắc của elip cần lập có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ với a > b > 0.

+ Trục Oy là đường trung trực của đoạn A₁A₂ nên O là trung điểm của A₁A₂ 

Suy ra OA₂ = $\frac{A_1{A}_2}{2}$$=\frac{768800}{2}=384400$.

Vì điểm A₂ nằm trên trục Ox về phía bên phải điểm O nên A₂(384 800; 0).

Điểm A₂ thuộc elip (E) nên

$\frac{384{800}^2}{a^2}+\frac{0^2}{b^2}=1\iff a^2=384{800}^2\Rightarrow a=384800$ (do a > 0).

+ Trục Ox là đường trung trực của đoạn B₁B₂ nên O là trung điểm của B₁B₂

Suy ra OB₂ = $\frac{B_1{B}_2}{2}$$=\frac{767619}{2}=383\mathrm{809,5}$.

Vì điểm B₂ nằm trên trục Oy về phía bên trên điểm O nên B₂(0; 383 809,5).

Elip (E) cắt trục Oy tại B₂(0; 338309,5), thay vào phương trình elip ta được:

$\frac{0^2}{a^2}+\frac{{\mathrm{338309,5}}^2}{b^2}=1\iff b^2={\mathrm{338309,5}}^2\Rightarrow b=\mathrm{338309,5}$ (do b > 0).

Do 384 800 > 383 809,5 nên a > b > 0 (thỏa mãn).

Vậy phương trình chính tắc của elip (E) là $\frac{x^2}{384{800}^2}+\frac{y^2}{383{\mathrm{809,5}}^2}=1$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Bài tập cuối chương 7

Thực hành phần mềm Geogebra