Giải SGK Toán 10 Cánh diều Thực hành phần mềm Geogebra

Giải Toán 10 Thực hành phần mềm Geogebra

Luyện tập 1 trang 105 Toán 10 Tập 2: Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn sau:

$\left\{\begin{array}{l}x-2y+3\le 0\\ x+3y>-2\\ x\le 0.\end{array}\right.$

Lời giải

Để biểu diễn hình học tập nghiệm của hệ bất phương trình trên ta làm như sau. Ta thực hiện theo các bước sau:

- Bước 1. Mở trang Geogebra.

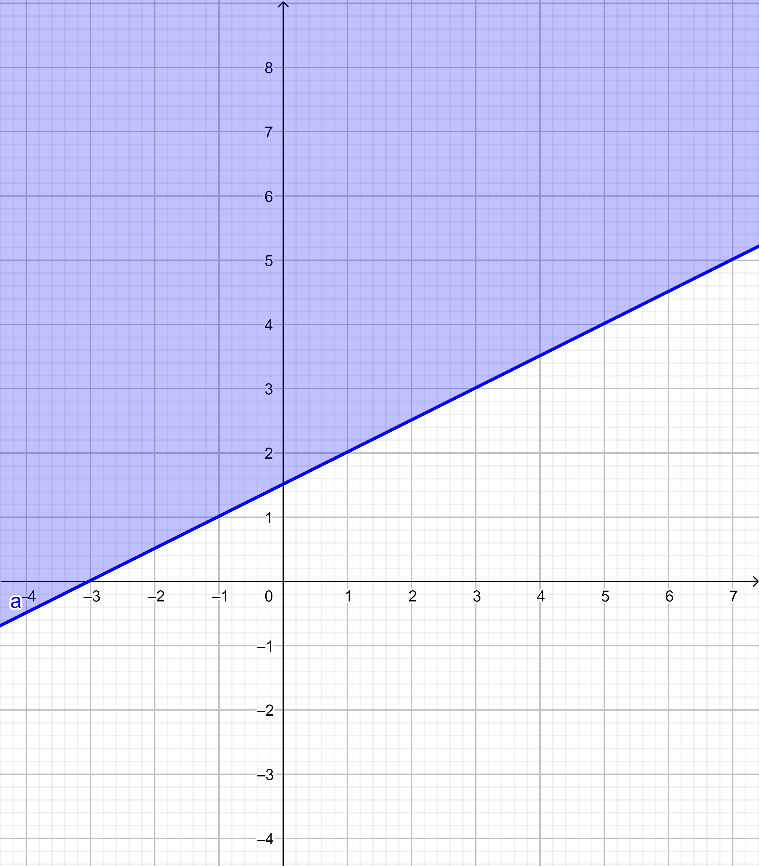
- Bước 2. Nhập bất phương trình x - 2y + 3 ≤ 0 (x - 2y + 3 <= 0) vào ô  và bấm Enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình x - 2y + 3 ≤ 0 là miền được tô màu.

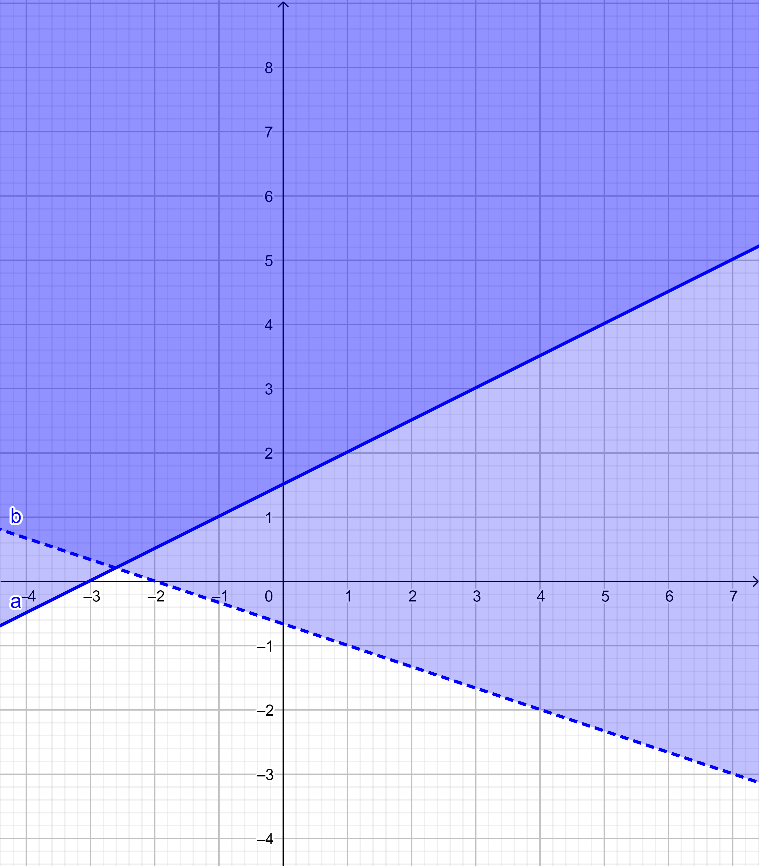
Bước 3. Nhập bất phương trình x + 3y > -2 vào ô  và bấm Enter, màn hình sẽ hiển thị như hình dưới. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng x + 3y = -2.

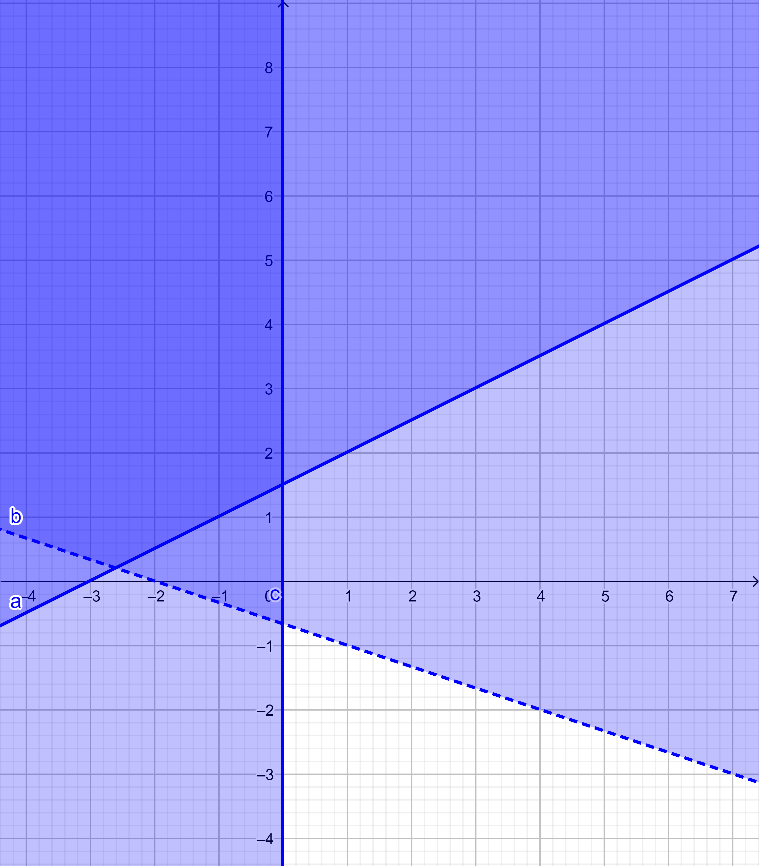
Bước 4. Nhập bất phương trình còn lại x ≤ 0 (x <= 0) vào ô  và bấm Enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của hệ là miền được tô màu đậm nhất. Các đường nét liền x - 2y + 3 = 0 và x = 0 nằm trong miền tô đậm nhất biểu thị các điểm nằm trên hai đường thẳng đó cũng thuộc miền nghiệm.

Luyện tập 2 trang 108 Toán 10 Tập 2: Vẽ hình trong mỗi trường hợp:

a) Vẽ hypebol biết hai tiêu điểm F₁(- 5; 0), F₂(5; 0) và điểm (3; 0) thuộc hypebol;

b) Vẽ parabol biết phương trình chính tắc: y² = 5x;

c) Vẽ elip tại các giá trị a = 3, b = 1 và a = 6, b = 3,5.

Lời giải

a) Để vẽ hypebol biết hai tiêu điểm F₁(-5; 0), F₂(5; 0) và điểm (3; 0) thuộc hypebol ta thực hiện theo các bước sau:

Bước 1. Mở trang Geogebra.

Bước 2. Nhập Hypebon((-5,0), (5,0), (3,0)) vào ô  rồi bấm Enter.

Khi đó màn hình sẽ hiển thị như hình dưới.

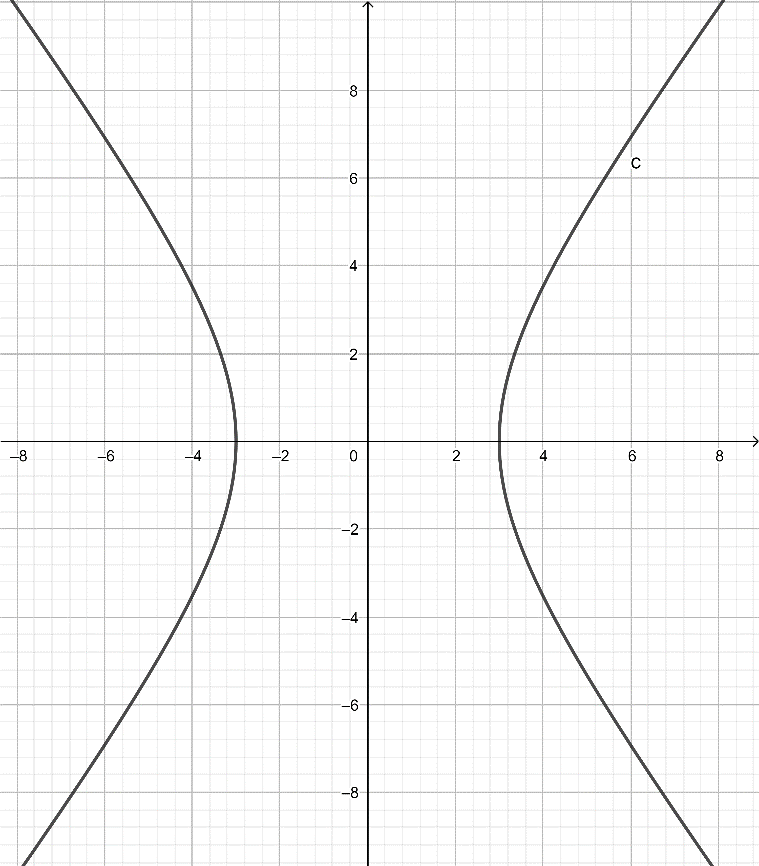
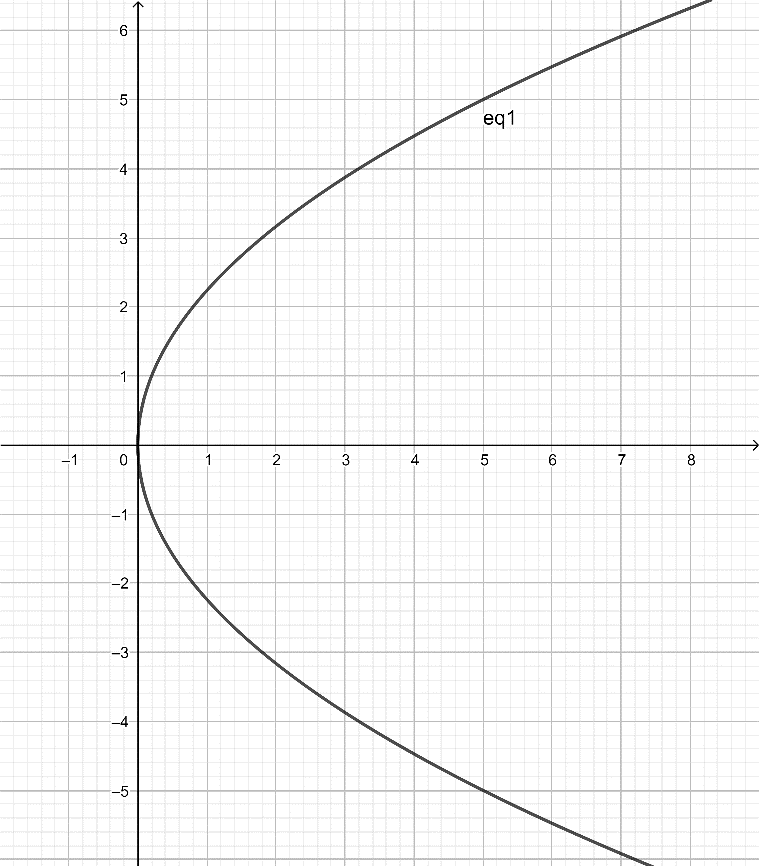
b) Để vẽ parabol có phương trình chính tắc là y² = 5x, ta thực hiện theo các bước sau:

Bước 1. Mở trang Geogebra.

Bước 2. Nhập y^2 = 5x vào ô  và bấm Enter, màn hình sẽ hiển thị như hình dưới.

c) Để vẽ elip tại các giá trị a = 3, b = 1 và a = 6, b = 3,5 ta thực hiện như sau:

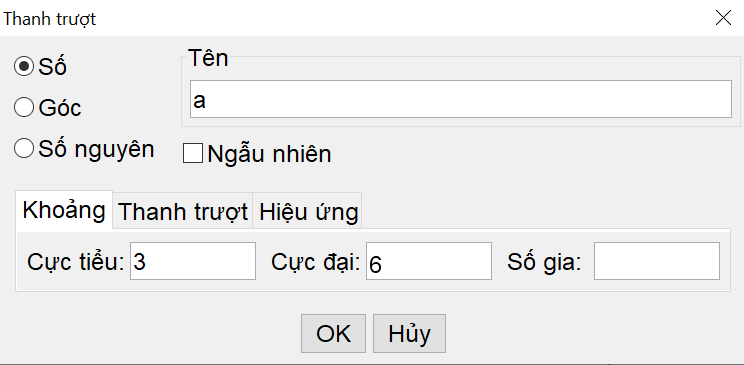
Bước 1. Chọn , nhấp chọn vào 1 khoảng trống bất kỳ trong vùng làm việc để đặt thanh trượt cho giá trị a. Ta thấy a nhận hai giá trị là 3 và 6 nên nhập cực tiểu là 3, cực đại là 6, sau đó chọn OK.

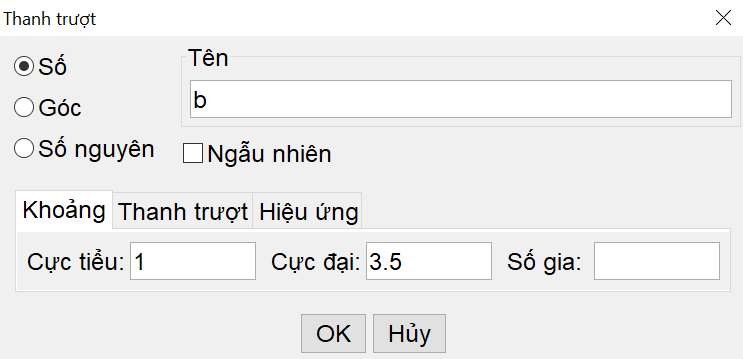
Bước 2. Nhấp chọn vào 1 khoảng trắng bất kỳ trong vùng làm việc để đặt thanh trượt cho giá trị b. Ta thấy b nhận hai giá trị là 1 và 3,5 nên nhập cực tiểu là 1, cực đại là 3,5 (3.5), sau đó chọn OK.

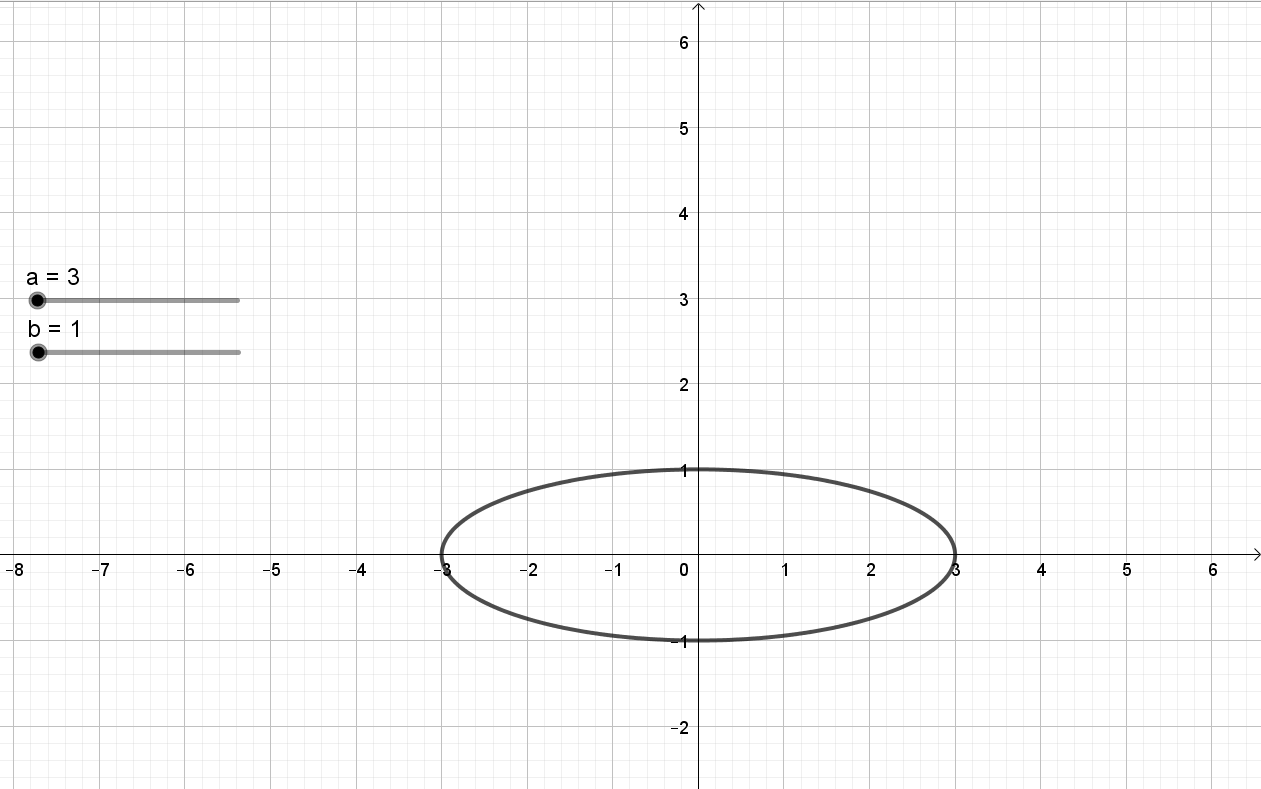
Bước 3. Chọn công cụ   để kéo thả đối tượng. Nhập x^2 / a^2 + y^2 / b^2 = 1 vào ô  và bấm Enter, màn hình sẽ hiển thị như hình dưới, ta thu được elip tại a = 3, b = 1.

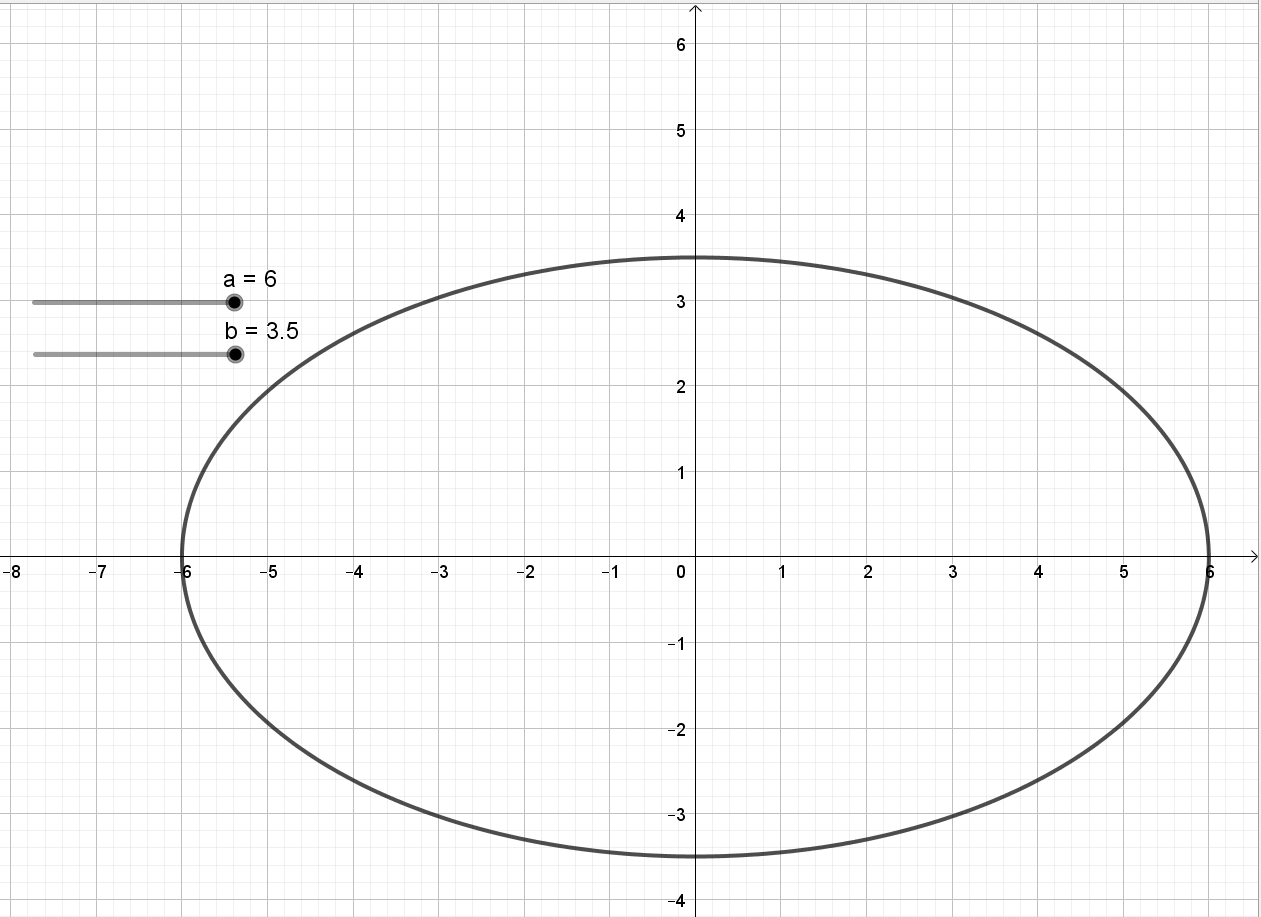
Bước 4. Trên thanh trượt của a, kéo a đến giá trị 6, trên thanh trượt b, kéo b đến giá trị 3,5 ta thu được elip tại a = 6, b = 3,5.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Bài tập cuối chương 7