Giải SGK Toán 10 (Cánh diều) Bài tập cuối chương 7 trang 103, 104

Giải Toán 10 Bài tập cuối chương 7 trang 103, 104

Bài 1 trang 103 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho A(3; 4); B(2; 5). Tọa độ của $\overrightarrow{AB}$ là:

A. (1; –1).           

B. (1; 1). 

C. (– 1; 1).  

D. (– 1; – 1).

Lời giải

Đáp án đúng là: C.

Ta có: $\overrightarrow{AB}=\left(2-3;5-4\right)$. Suy ra $\overrightarrow{AB}=\left(-1;1\right)$.

Bài 2 trang 103 Toán 10 Tập 2: Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng Δ: 2x – 3y + 4 = 0?

A. $\overrightarrow{n_1}=\left(3;2\right)$.

B. $\overrightarrow{n_2}=\left(2;3\right)$.

C. $\overrightarrow{n_3}=\left(3;-2\right)$.

D. $\overrightarrow{n_4}=\left(2;-3\right)$.

Lời giải

Đáp án đúng là: D.

Đường thẳng ∆: 2x – 3y + 4 = 0 có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$

Bài 3 trang 103 Toán 10 Tập 2: Tọa độ tâm I của đường tròn (C): (x + 6)² + (y – 12)² = 81 là:

A. (6; – 12).              

B. (– 6; 12).              

C. (– 12; 6).              

D.(12; – 6).

Lời giải

Đáp án đúng là: B.

Ta có: (x + 6)² + (y – 12)² = 81

⇔ [x – (– 6)]² + (y – 12)² = 9².

Vậy đường tròn (C) có tâm I(– 6; 12).

Bài 4 trang 103 Toán 10 Tập 2: Khoảng cách từ điểm A(1; 1) đến đường thẳng Δ: 3x + 4y + 13 = 0 bằng:

A. 1.                      

B. 2.                       

C. 3.                      

 D. 4.

Lời giải

Đáp án đúng là: D.

Khoảng cách từ điểm A(1; 1) đến đường thẳng Δ: 3x + 4y + 13 = 0 là

$d\left(A,\Delta \right)=\frac{\left|3.1+4.1+13\right|}{\sqrt{3^2+4^2}}=\frac{20}{5}=4$.

Bài 5 trang 103 Toán 10 Tập 2: Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có M(2; 1), N(– 1; 3), P(4; 2).

a) Tìm tọa độ của các vectơ $\overrightarrow{OM},\overrightarrow{MN},\overrightarrow{MP}$;

b) Tính tích vô hướng $\overrightarrow{MN}.\overrightarrow{MP}$;

c) Tính độ dài các đoạn thẳng MN, MP;

d) Tính $cos\widehat{NMP}$;

e) Tìm tọa độ trung điểm I của NP và trọng tâm G của tam giác MNP.

Lời giải

a) Tọa độ của vectơ $\overrightarrow{OM}$ chính là tọa độ của điểm M(2; 1) nên $\overrightarrow{OM}=\left(2;1\right)$.

Ta có: $\overrightarrow{MN}=\left(-1-2;3-1\right)$, suy ra $\overrightarrow{MN}=\left(-3;2\right)$.

Và $\overrightarrow{MP}=\left(4-2;2-1\right)$, suy ra $\overrightarrow{MP}=\left(2;1\right)$.

b) $\overrightarrow{MN}.\overrightarrow{MP}=\left(-3\right).2+2.1=-6+2=-4$.

c) Độ dài đoạn thẳng MN là:

$MN=\left|\overrightarrow{MN}\right|=\sqrt{{\left(-3\right)}^2+2^2}=\sqrt{13}$.

Độ dài đoạn thẳng MP là:

$MP=\left|\overrightarrow{MP}\right|=\sqrt{2^2+1^2}=\sqrt{5}$.

d) Ta có: $cos\widehat{NMP}=cos\left(\overrightarrow{MN},\overrightarrow{MP}\right)$$=\frac{\overrightarrow{MN}.\overrightarrow{MP}}{\left|\overrightarrow{MN}\right|.\left|\overrightarrow{MP}\right|}=\frac{-4}{\sqrt{13}.\sqrt{5}}=\frac{-4\sqrt{65}}{65}$.

Vậy $cos\widehat{NMP}=\frac{-4\sqrt{65}}{65}$.

e) Tọa độ trung điểm I của NP là $\left\{\begin{array}{l}{x}_I=\frac{x_N+x_P}{2}=\frac{\left(-1\right)+4}{2}=\frac{3}{2}\\ y_I=\frac{y_N+y_P}{2}=\frac{3+2}{2}=\frac{5}{2}\end{array}\right.$.

Vậy $I\left(\frac{3}{2};\frac{5}{2}\right)$.

Tọa độ trọng tâm G của tam giác MNP là $\left\{\begin{array}{l}{x}_G=\frac{x_M+x_N+x_P}{3}=\frac{2+\left(-1\right)+4}{3}=\frac{5}{3}\\ y_G=\frac{y_M+y_N+y_P}{3}=\frac{1+3+2}{3}=\frac{6}{3}=2\end{array}\right.$ .

Vậy $G\left(\frac{5}{3};2\right)$.

Bài 6 trang 103 Toán 10 Tập 2: Lập phương trình tổng quát và phương trình tham số của đường thẳng d trong mỗi trường hợp sau:

a) d đi qua điểm A(– 3; 2) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$;

b) d đi qua điểm B(– 2; – 5) và có một vectơ chỉ phương là $\overrightarrow{u}=\left(-7;6\right)$;

c) d đi qua hai điểm C(4; 3) và D(5; 2).

Lời giải

a) + Đường thẳng d đi qua điểm A(– 3; 2) và có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$.

Vậy phương trình tổng quát của đường thẳng d là:

2[x – (– 3)] – 3(y – 2) = 0 hay 2x – 3y + 12 = 0.

 + Đường thẳng d có một vectơ pháp tuyến là $\overrightarrow{n}=\left(2;-3\right)$ suy ra d có một vectơ chỉ phương là $\overrightarrow{u}=\left(3;2\right)$.

Vậy phương trình tham số của đường thẳng d là $\left\{\begin{array}{l}x=-3+3t\\ y=2+2t\end{array}\right.$ (t là tham số).

b) + Đường thẳng d đi qua điểm B(– 2; – 5) và có một vectơ chỉ phương là $\overrightarrow{u}=\left(-7;6\right)$.

Vậy phương trình tham số của đường thẳng d là $\left\{\begin{array}{l}x=-2-7t\\ y=-5+6t\end{array}\right.$ (t là tham số).

+ Đường thẳng d có một vectơ chỉ phương là $\overrightarrow{u}=\left(-7;6\right)$ nên d có một vectơ pháp tuyến là $\overrightarrow{n}=\left(6;7\right)$.

Vậy phương trình tổng quát của đường thẳng d là:

6(x + 2) + 7(y + 5) = 0 hay 6x + 7y + 47 = 0.

c) Ta có: $\overrightarrow{CD}=\left(5-4;2-3\right)$, suy ra $\overrightarrow{CD}=\left(1;-1\right)$.

+ Đường thẳng d đi qua 2 điểm C, D nên có một vectơ chỉ phương là $\overrightarrow{u}=\overrightarrow{CD}=\left(1;-1\right)$.

Vậy phương trình tham số của đường thẳng d là $\left\{\begin{array}{l}x=4+t\\ y=3-t\end{array}\right.$ (t là tham số).

+ Đường thẳng d có vectơ chỉ phương là $\overrightarrow{u}=\left(1;-1\right)$ nên d có một vectơ pháp tuyến là $\overrightarrow{n}=\left(1;\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}1\right)$.

Vậy phương trình tổng quát của đường thẳng d là:

1(x – 4) + 1(y – 3) = 0 hay x + y – 7 = 0.

Bài 7 trang 103 Toán 10 Tập 2: Lập phương trình đường tròn (C) trong mỗi trường hợp sau:

a) (C) có tâm I(– 4; 2) và bán kính R = 3;

b) (C) có tâm P(3; – 2) và đi qua điểm E(1; 4);

c) (C) có tâm Q(5; – 1) và tiếp xúc với đường thẳng Δ: 3x + 4y – 1 = 0;

d) (C) đi qua ba điểm A(– 3; 2), B(– 2; – 5) và D(5; 2).

Lời giải

a) Đường tròn (C) có tâm I(– 4; 2) và bán kính R = 3.

Vậy phương trình đường tròn (C) là

[x – (– 4)]² + (y – 2)² = 3² hay (x + 4)² + (y – 2)² = 9.

b) Đường tròn (C) có tâm P(3; – 2) và đi qua điểm E(1; 4).

Do đó bán kính đường tròn (C) là

R = PE = $\sqrt{{\left(1-3\right)}^2+{\left(4-\left(-2\right)\right)}^2}=\sqrt{40}$.

Vậy phương trình đường tròn (C) là

${\left(x-3\right)}^2+{\left[y-\left(-2\right)\right]}^2={\left(\sqrt{40}\right)}^2$ hay (x – 3)² + (y + 2)² = 40.

c) Đường tròn (C) có tâm Q(5; – 1) và tiếp xúc với đường thẳng Δ: 3x + 4y – 1 = 0.

Do đó bán kính của đường tròn (C) là

R = d(Q, ∆) = $\frac{\left|3.5+4.\left(-1\right)-1\right|}{\sqrt{3^2+4^2}}=\frac{10}{5}=2$.

Vậy phương trình đường tròn (C) là

(x – 5)² + [y – (– 1)]² = 2² hay (x – 5)² + (y + 1)² = 4.

d) Đường tròn (C) đi qua ba điểm A(– 3; 2), B(– 2; – 5) và D(5; 2).

 Giả sử tâm của đường tròn là điểm I(a; b).

Ta có IA = IB = ID ⇔ IA² = IB² = ID².

Vì IA² = IB², IB² = ID² nên

$\left\{\begin{array}{l}{\left(-3-a\right)}^2+{\left(2-b\right)}^2={\left(-2-a\right)}^2+{\left(-5-b\right)}^2\\ {\left(-2-a\right)}^2+{\left(-5-b\right)}^2={\left(5-a\right)}^2+{\left(2-b\right)}^2\end{array}\right.$

$\iff \left\{\begin{array}{l}{a}^2+6a+9+b^2-4b+4=a^2+4a+4+b^2+10b+25\\ a^2+4a+4+b^2+10b+25=a^2-10a+25+b^2-4b+4\end{array}\right.$

$\iff \left\{\begin{array}{l}2a-14b=16\\ 14a+14b=0\end{array}\right.\iff \left\{\begin{array}{l}a=1\\ b=-1\end{array}\right.$

Đường tròn tâm I(1; – 1) có bán kính

R = IA = $\sqrt{{\left(-3-a\right)}^2+{\left(2-b\right)}^2}$$=\sqrt{{\left(-3-1\right)}^2+{\left(2+1\right)}^2}=5$

Phương trình đường tròn (C) là (x – 1)² + [y – (– 1)]² = 5².

Vậy phương trình đường tròn (C) là (x – 1)² + (y + 1)² = 25.

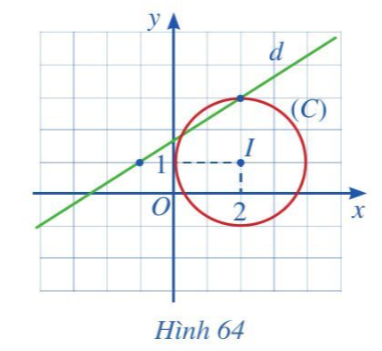
Bài 8 trang 104 Toán 10 Tập 2: Quan sát Hình 64 và thực hiện các hoạt động sau:

a) Lập phương trình đường thẳng d;

b) Lập phương trình đường tròn (C);

c) Lập phương trình tiếp tuyến của đường tròn (C) tại điểm $M\left(2+\sqrt{2};1+\sqrt{2}\right)$.

Lời giải

a) Từ Hình 64 ta thấy đường thẳng d đi qua hai điểm A(– 1; 1) và B(2; 3).

Ta có: $\overrightarrow{AB}=\left(3;2\right)$.

Đường thẳng d đi qua điểm A(– 1; 1) và có một vectơ chỉ phương là $\overrightarrow{u}=\overrightarrow{AB}=\left(3;2\right)$.

Vậy phương trình tham số của đường thẳng d là $\left\{\begin{array}{l}x=-1+3t\\ y=1+2t\end{array}\right.$ (t là tham số).

b) Từ Hình 64 ta thấy đường tròn (C) có tâm I(2; 1) và bán kính R = 2.

Vậy phương trình đường tròn (C) là

(x – 2)² + (y – 1)² = 2² hay (x – 2)² + (y – 1)² = 4.

c) Phương trình tiếp tuyến của đường tròn (C) tại điểm $M\left(2+\sqrt{2};1+\sqrt{2}\right)$ là

$\left(2+\sqrt{2}-2\right)\left[x-\left(2+\sqrt{2}\right)\right]+\left(1+\sqrt{2}-1\right)\left[y-\left(1+\sqrt{2}\right)\right]=0$

$\iff \sqrt{2}x-2\sqrt{2}-2+\sqrt{2}y-\sqrt{2}-2=0$

$\iff \sqrt{2}x+\sqrt{2}y-3\sqrt{2}-4=0$

$\iff x+y-3-2\sqrt{2}=0$.

Vậy phương trình tiếp tuyến là $x+y-3-2\sqrt{2}=0$.

Bài 9 trang 104 Toán 10 Tập 2: Cho hai đường thẳng:

${\Delta }_1:\sqrt{3}x+y-4=\mathrm{0,}{\Delta }_2:x+\sqrt{3}y-2\sqrt{3}=0.$

a) Tìm tọa độ giao điểm của hai đường thẳng Δ₁ và Δ₂.

b) Tính số đo góc giữa hai đường thẳng Δ₁ và Δ₂.

Lời giải

a) Tọa độ giao điểm của hai đường thẳng Δ₁ và Δ₂ là nghiệm của hệ phương trình

$\left\{\begin{array}{l}\sqrt{3}x+y-4=0\\ x+\sqrt{3}y-2\sqrt{3}=0\end{array}\right.$.

Giải hệ phương trình:

$\left\{\begin{array}{l}\sqrt{3}x+y-4=0\\ x+\sqrt{3}y-2\sqrt{3}=0\end{array}\right.$$\iff \left\{\begin{array}{l}\sqrt{3}x+y=4\left(1\right)\\ \sqrt{3}x+3y=6\left(2\right)\end{array}\right.$

Lấy (2) – (1) ta được: 3y – y = 6 – 4 ⇔ 2y = 2 ⇔ y = 1.

Thay y = 1 vào (1) ta được: $\sqrt{3}x+1=4\iff \sqrt{3}x=3\iff x=\sqrt{3}$.

Hệ trên có nghiệm duy nhất $\left(\sqrt{3};1\right)$.

Vậy tọa độ giao điểm của hai đường thẳng Δ₁ và Δ₂ là $\left(\sqrt{3};1\right)$.

b) Đường thẳng ∆₁ có vectơ pháp tuyến là $\overrightarrow{n_1}=\left(\sqrt{3};1\right)$, đường thẳng ∆₂ có vectơ pháp tuyến là $\overrightarrow{n_2}=\left(1;\sqrt{3}\right)$.

Ta có: $co\text{s}\left({\Delta }_1,{\Delta }_2\right)=\left|cos\left(\overrightarrow{n_1},\overrightarrow{n_2}\right)\right|$

$=\frac{\left|\overrightarrow{n_1}.\overrightarrow{n_2}\right|}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{\left|\sqrt{3}.1+1.\sqrt{3}\right|}{\sqrt{{\left(\sqrt{3}\right)}^2+1^2}.\sqrt{1^2+{\left(\sqrt{3}\right)}^2}}=\frac{2\sqrt{3}}{2.2}=\frac{\sqrt{3}}{2}$.

Vậy (∆₁, ∆₂) = 30°.

Bài 10 trang 104 Toán 10 Tập 2: Cho biết mỗi đường conic có phương trình dưới đây là đường conic dạng nào (elip, hypebol, parabol) và tìm tọa độ tiêu điểm của đường conic đó.

a) y² = 18x;

b) $\frac{x^2}{64}+\frac{y^2}{25}=1$;

c) $\frac{x^2}{9}-\frac{y^2}{16}=1$.

Lời giải

a) Ta có: y² = 18x ⇔ y² = 2 . 9 . x

Vậy phương trình trên là phương trình của parabol với p = 9.

Ta có $\frac{p}{2}=\frac{9}{2}$.

Vậy tọa độ tiêu điểm của parabol là $F\left(\frac{9}{2};0\right)$.

b) $\frac{x^2}{64}+\frac{y^2}{25}=1$$\iff \frac{x^2}{8^2}+\frac{y^2}{5^2}=1$.

Vậy phương trình trên là phương trình của elip với a = 8, b = 5 thỏa mãn a > b > 0.

Suy ra c² = a² – b² = 64 – 25 = 39.

Do đó, c = $\sqrt{39}$.

Vậy tọa độ các tiêu điểm của elip là $F_1\left(-\sqrt{39};0\right),F_2\left(\sqrt{39};0\right)$.

c) $\frac{x^2}{9}-\frac{y^2}{16}=1\iff \frac{x^2}{3^2}-\frac{y^2}{4^2}=1$.

Vậy phương trình trên là phương trình của hypebol với a = 3, b = 4 thỏa mãn a > 0, b > 0.

Suy ra c² = a² + b² = 9 + 16 = 25.

Do đó, c = 5.

Vậy tọa độ các tiêu điểm của hypebol là F₁(– 5; 0) và F₂(5; 0).

Bài 11 trang 104 Toán 10 Tập 2: Cho tam giác AF₁F₂, trong đó A(0; 4), F₁(– 3; 0), F₂(3; 0).

a) Lập phương trình tổng quát của các đường thẳng AF₁ và AF₂.

b) Lập phương trình đường tròn ngoại tiếp của tam giác AF₁F₂.

c) Lập phương trình chính tắc của elip (E) có hai tiêu điểm là F₁, F₂ sao cho (E) đi qua A.

Lời giải

a) +) $\overrightarrow{A{F}_1}=\left(-3;-4\right)$ là một vectơ chỉ phương của đường thẳng AF₁.

Suy ra đường thẳng AF₁ có một vectơ pháp tuyến là $\overrightarrow{n_1}=\left(4;-3\right)$.

Vậy phương trình tổng quát đường thẳng AF₁ là:

4(x – 0) – 3(y – 4) = 0 hay 4x – 3y + 12 = 0.

+) $\overrightarrow{A{F}_2}=\left(3;-4\right)$ là một vectơ chỉ phương của đường thẳng AF₂.

Suy ra đường thẳng AF₂ có một vectơ pháp tuyến là $\overrightarrow{n_2}=\left(4;3\right)$.

Vậy phương trình tổng quát đường thẳng AF₂ là:

4(x – 0) + 3(y – 4) = 0 hay 4x + 3y – 12 = 0.

b) Đường tròn ngoại tiếp tam giác AF₁F₂ chính là đường tròn đi qua 3 điểm A, F₁, F₂.

Giả sử tâm của đường tròn là điểm I(a; b).

Ta có IA = IF₁ = IF₂ ⇔ IA² = $I{F}_1^2$= $I{F}_2^2$ .

Vì IA² = $I{F}_1^2$, $I{F}_1^2$ = $I{F}_2^2$ nên

$\left\{\begin{array}{l}{\left(0-a\right)}^2+{\left(4-b\right)}^2={\left(-3-a\right)}^2+{\left(0-b\right)}^2\\ {\left(-3-a\right)}^2+{\left(0-b\right)}^2={\left(3-a\right)}^2+{\left(0-b\right)}^2\end{array}\right.$

$\iff \left\{\begin{array}{l}{a}^2+b^2-8b+16=a^2+6a+9+b^2\\ a^2+6a+9+b^2=a^2-6a+9+b^2\end{array}\right.$

$\iff \left\{\begin{array}{l}6a+8b=7\\ 12a=0\end{array}\right.\iff \left\{\begin{array}{l}a=0\\ b=\frac{7}{8}\end{array}\right.$

Đường tròn tâm $I\left(0;\frac{7}{8}\right)$ có bán kính

R = IA = $\sqrt{{\left(0-a\right)}^2+{\left(4-b\right)}^2}$$=\sqrt{{\left(4-\frac{7}{8}\right)}^2}=\frac{25}{8}$.

Phương trình đường tròn (C) là ${\left(x-0\right)}^2+{\left(y-\frac{7}{8}\right)}^2={\left(\frac{25}{8}\right)}^2$.

Vậy phương trình đường tròn (C) là $x^2+{\left(y-\frac{7}{8}\right)}^2=\frac{625}{64}$.

c) Phương trình chính tắc của elip (E) có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\left(a>b>0\right)$.

Elip (E) đi qua điểm A(0; 4) nên $\frac{0^2}{a^2}+\frac{4^2}{b^2}=1\iff b^2=4^2\Rightarrow b=4\left(dob>0\right)$.

Elip (E) có hai tiêu điểm là F₁(– 3; 0), F₂(3; 0) nên c = 3.

Ta có: a² – b² = c² 

Suy ra a² – 4² = 3² 

⇔ a² = 25.

Do đó, a = 5 (do a > 0).

Khi đó a > b > 0, vậy a = 5, b = 4 thỏa mãn.

Vậy phương trình elip (E) cần lập là $\frac{x^2}{5^2}+\frac{y^2}{4^2}=1hay\frac{x^2}{25}+\frac{y^2}{16}=1$.

Bài 12 trang 104 Toán 10 Tập 2: Trên màn hình ra đa của đài kiểm soát không lưu sân bay A có hệ trục toạ độ Oxy (Hình 65), trong đó đơn vị trên mỗi trục tính theo ki-lô-mét và đài kiểm soát được coi là gốc toạ độ O(0 ; 0). Nếu máy bay bay trong phạm vi cách đài kiểm soát 500 km thì sẽ hiển thị trên màn hình ra đa như một điểm chuyển động trong mặt phẳng với hệ trục toạ độ Oxy.

Một máy bay khởi hành từ sân bay B lúc 14 giờ. Sau thời gian t (giờ), vị trí của máy bay được xác định bởi điểm M có toạ độ như sau:

$\left\{\begin{array}{l}x=\frac{1600}{3}-\frac{1400}{3}t\\ y=\frac{1900}{3}-\frac{1400}{3}t\end{array}\right.$.

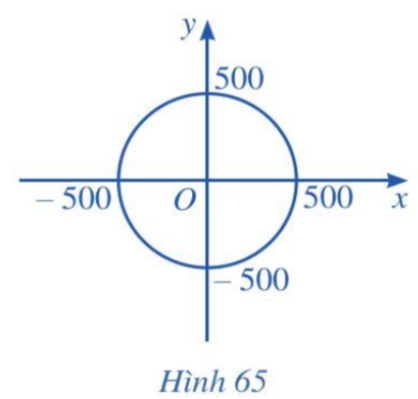
a) Tìm vị trí của máy bay lúc 14 giờ 30 phút. Thời điểm này máy bay đã xuất hiện trên màn hình ra đa chưa?

b) Lúc mấy giờ máy bay bay gần đài kiểm soát không lưu nhất? Tính khoảng cách giữa máy bay và đài kiểm soát không lưu lúc đó.

c) Máy bay ra khỏi màn hình ra đa vào thời gian nào?

Lời giải

a) Lúc 14 giờ 30 phút máy bay đã bay được:

14 giờ 30 phút – 14 giờ = 30 phút = 0,5 giờ.

Vị trí của máy bay tại thời điểm t = 0,5 là: $\left\{\begin{array}{l}x=\frac{1600}{3}-\frac{1400}{3}\mathrm{.0,5}=300\\ y=\frac{1900}{3}-\frac{1400}{3}\mathrm{.0,5}=400\end{array}\right.$.

Do đó, vị trí của máy bay lúc 14 giờ 30 phút ở tại điểm M(300; 400).

Ta có: $OM=\sqrt{{\left(300-0\right)}^2+{\left(400-0\right)}^2}=500$.

Khi đó, khoảng cách từ đài kiểm soát không lưu O đến vị trí M của máy bay lúc 14 giờ 30 phút là 500 km.

Vậy tại thời điểm này, máy bay đã xuất hiện trên màn hình ra đa.

b) Máy bay bay trên đường thẳng ∆ có phương trình tham số là: $\left\{\begin{array}{l}x=\frac{1600}{3}-\frac{1400}{3}t\\ y=\frac{1900}{3}-\frac{1400}{3}t\end{array}\right.$.

Gọi N là hình chiếu của O đến đường thẳng ∆.

Khi đó ON là khoảng cách ngắn nhất từ O đến ∆.

Do đó, tại vị trí N máy bay bay gần đài kiểm soát không lưu O nhất.

Vì N thuộc ∆ nên gọi $N\left(\frac{1600}{3}-\frac{1400}{3}t;\frac{1900}{3}-\frac{1400}{3}t\right)$.

Suy ra $\overrightarrow{ON}=\left(\frac{1600}{3}-\frac{1400}{3}t;\frac{1900}{3}-\frac{1400}{3}t\right)$.

Mà đường thẳng ∆ có một vectơ chỉ phương là $\overrightarrow{u_{\Delta }}=\left(1;1\right)$.

Mà ON ⊥ ∆

Do đó, $\overrightarrow{ON}.\overrightarrow{u_{\Delta }}=0$

$\iff \left(\frac{1600}{3}-\frac{1400}{3}t\right).1+\left(\frac{1900}{3}-\frac{1400}{3}t\right).1=0$

$\iff t=\frac{5}{4}$.

Suy ra: $\frac{1600}{3}-\frac{1400}{3}.\frac{5}{4}=-50$; $\frac{1900}{3}-\frac{1400}{3}.\frac{5}{4}=50$.

Vậy N(– 50; 50).

Suy ra $ON=\sqrt{{\left(-50\right)}^2+{50}^2}=50\sqrt{2}$.

Mặt khác: t = $\frac{5}{4}$ giờ = 1 giờ 15 phút.

Vậy máy bay bay gần đài kiểm soát không lưu nhất lúc:

14 giờ + 1 giờ 15 phút = 15 giờ 15 phút

và khoảng cách giữa máy bay và đài kiểm soát không lưu lúc này là $50\sqrt{2}$ km.

c) Gọi $M\left(\frac{1600}{3}-\frac{1400}{3}t;\frac{1900}{3}-\frac{1400}{3}t\right)$ là vị trí máy bay ra khỏi màn hình ra đa.

Khi đó OM > 500 km.

Ta có: $OM=\sqrt{{\left(\frac{1600}{3}-\frac{1400}{3}t\right)}^2+{\left(\frac{1900}{3}-\frac{1400}{3}t\right)}^2}$.

Vậy OM > 500 ⇔ $\sqrt{{\left(\frac{1600}{3}-\frac{1400}{3}t\right)}^2+{\left(\frac{1900}{3}-\frac{1400}{3}t\right)}^2}>500$

⇒ ${\left(\frac{1600}{3}-\frac{1400}{3}t\right)}^2+{\left(\frac{1900}{3}-\frac{1400}{3}t\right)}^2>250000$

$\iff \frac{3920000}{9}{t}^2-\frac{9800000}{9}t+\frac{3920000}{9}>0$

$\iff 2t^2-5t+2>0$

$\iff \left[\begin{array}{l}t<\frac{1}{2}\\ t>2\end{array}\right.$

Ta có $\frac{1}{2}$ giờ = 30 phút.

14 giờ + 30 phút = 14 giờ 30 phút; 14 giờ + 2 giờ = 16 giờ.  

Vậy máy bay bay ra khỏi màn hình ra đa vào khoảng thời gian từ 14 giờ đến trước 14 giờ 30 phút và sau 16 giờ.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Thực hành phần mềm Geogebra