Cho parabol (P) với tiêu điểm F và đường chuẩn ∆. Cũng như elip, để lập phương trình của (P), trước tiên ta sẽ chọn hệ trục tọa độ Oxy thuận tiện nhất

Hoạt động 6 trang 99, 100 Toán 10 Tập 2: Cho parabol (P) với tiêu điểm F và đường chuẩn ∆. Cũng như elip, để lập phương trình của (P), trước tiên ta sẽ chọn hệ trục tọa độ Oxy thuận tiện nhất.

Kẻ FH vuông góc với ∆ (H ∈ ∆). Đặt FH = p > 0. Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm đoạn thẳng FH và F nằm trên tia Ox (Hình 56).

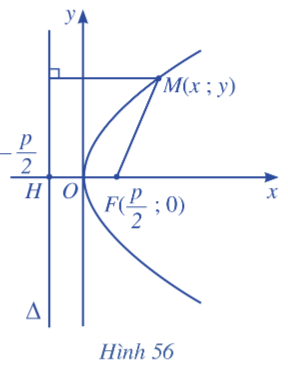
Suy ra: $F\left(\frac{p}{2};0\right),H\left(-\frac{p}{2};0\right)$ và phương trình đường thẳng ∆ là $x+\frac{p}{2}=0.$

Do đó khoảng cách từ M(x; y) ∈ (P) đến đường thẳng ∆ là $\left|x+\frac{p}{2}\right|$.

Ta có: M(x; y) ∈ (P) khi và chỉ khi độ dài MF bằng khoảng cách từ M tới ∆, tức là:

$\sqrt{{\left(x-\frac{p}{2}\right)}^2+y^2}=\left|x+\frac{p}{2}\right|\iff {\left(x-\frac{p}{2}\right)}^2+y^2={\left(x+\frac{p}{2}\right)}^2$

$\iff y^2={\left(x+\frac{p}{2}\right)}^2-{\left(x-\frac{p}{2}\right)}^2\iff y^2=2px$.

Trả lời

Xem hoạt động để nhận biết được cách xây dựng phương trình chính tắc của đường parabol.

Xem thêm lời giải bài tập SGK Toán lớp 10 Cánh diều hay, chi tiết khác:

Bài 3: Phương trình đường thẳng

Bài 4: Vị trí tương đối và góc giữa hai đường thẳng. Khoảng cách từ một điểm đến một đường thẳng

Bài 5: Phương trình đường tròn

Bài 6: Ba đường conic

Bài tập cuối chương 7

Thực hành phần mềm Geogebra