Câu hỏi:
03/04/2024 17
Gọi S là tập hợp tất cả các số thực m để phương trình \[4{\cos ^3}x + 2\cos 2x + 2 = \left( {m + 3} \right)\cos x\] có đúng 5 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]. Kết luận nào sau đây đúng?
A. \[S \subset \left( {0;7} \right)\]
B. \[\left( { - 2;8} \right) \subset S\]
C. \[S \cap \left( {0; + \infty } \right) = \emptyset \]
D. \[S \subset \left( { - 3;5} \right)\]
Trả lời:
Giải bởi Vietjack
Đáp án D
Phương pháp giải:
Giải chi tiết:
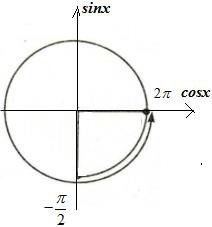
Ta có:
\[{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 4{\cos ^3}x + 2\cos 2x + 2 = \left( {m + 3} \right)\cos x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (*){\mkern 1mu} \]
\[ \Leftrightarrow 4{\cos ^3}x + 4{\cos ^2}x - \left( {m + 3} \right)\cos x = 0\]
\[ \Leftrightarrow \left( {4{{\cos }^2}x + 2\cos x - \left( {m + 3} \right)} \right).\cos x = 0\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{4{{\cos }^2}x + 4\cos x - \left( {m + 3} \right) = 0{\mkern 1mu} {\mkern 1mu} (1)}\\{\cos x = 0{\mkern 1mu} {\mkern 1mu} (2)}\end{array}} \right.\]
Phương trình \[(2) \Leftrightarrow x = \frac{\pi }{2} + k\pi {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\]. Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2}}\\{x = \frac{{3\pi }}{2}}\end{array}} \right.\]
Thay \[\cos x = 0\] vào (1): \[{4.0^2} + 4.0 - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\]
+) Với \[m = - 3\]:
Phương trình \[(1) \Leftrightarrow 4{\cos ^2}x + 4\cos x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos x = 0}\\{\cos x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k\pi }\\{x = \pi + k2\pi }\end{array}} \right.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} ,k \in \mathbb{Z}\]
Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow x \in \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\}\]
Phương trình \[(*)\] có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] là \[\left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\} \Rightarrow m = - 3\] không thỏa mãn
+) Với \[m \ne - 3\]: Phương trình (1) không có nghiệm \[x = \frac{\pi }{2},{\mkern 1mu} {\mkern 1mu} x = \frac{{3\pi }}{2}\]. Khi đó, để (*) có đúng 5 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] thì phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]
Đặt \[\cos x = t\], (1) trở thành: \[4{t^2} + 4t - \left( {m + 3} \right) = 0\] (3)
Phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]⇔ Phương trình (3) có 2 nghiệm \[{t_1},{\mkern 1mu} {\mkern 1mu} {t_2}{\mkern 1mu} {\mkern 1mu} \left( {{t_1} \le {t_2}} \right)\] thỏa mãn:
hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\], hoặc \[{t_1} = {t_2} \in \left( {0;1} \right)\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right.\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right.\]
TH1: \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\]
\[ \Rightarrow 4.{\left( { - 1} \right)^2} + 4.\left( { - 1} \right) - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\] (loại)
TH2: \[{t_1} = {t_2} \in \left( {0;1} \right)\]
\[ \Rightarrow \Delta ' = 0 \Leftrightarrow 4 + 4\left( {m + 3} \right) \Leftrightarrow 4m + 16 = 0 \Leftrightarrow m = - 4\]
Khi đó, (3) có 2 nghiệm \[{t_1} = {t_2} = - \frac{1}{2} \notin \left( {0;1} \right){\mkern 1mu} {\mkern 1mu} \Rightarrow m = - 4\]: không thỏa mãn
TH3:
\[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right. \Leftrightarrow 0 < {t_1} < 1 < {t_2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{{t_1}{t_2} - \left( {{t_1} + {t_2}} \right) + 1 < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} > 0}\\{ - \frac{4}{4} > 0}\\{1 - \left( { - \frac{4}{4}} \right) - \frac{{m + 3}}{4} < 0}\end{array}} \right. \Leftrightarrow m \in \emptyset \]
TH4:
\[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right. \Leftrightarrow {t_1} < - 1 < 0 < {t_2} < 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} < 0}\\{\left( {{t_1} + 1} \right)\left( {{t_2} + 1} \right) < 0}\\{\left( {{t_1} - 1} \right) + \left( {{t_2} - 1} \right) < 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} < 0}\\{ - \frac{{m + 3}}{4} + \left( { - \frac{4}{4}} \right) + 1 < 0}\\{ - \frac{4}{4} - 2 < 0}\\{ - \frac{{m + 3}}{4} - \left( { - \frac{4}{4}} \right) + 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 4}\\{m > - 3}\\{m < 5}\end{array}} \right. \Leftrightarrow m \in \left( { - 3;5} \right)\]
Vậy, tập các giá trị thực của m thỏa mãn yêu cầu đề bài là: \[S = \left( { - 3;5} \right)\]
Đáp án D
Phương pháp giải:
Giải chi tiết:
Ta có:
\[{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} 4{\cos ^3}x + 2\cos 2x + 2 = \left( {m + 3} \right)\cos x{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} (*){\mkern 1mu} \]
\[ \Leftrightarrow 4{\cos ^3}x + 4{\cos ^2}x - \left( {m + 3} \right)\cos x = 0\]
\[ \Leftrightarrow \left( {4{{\cos }^2}x + 2\cos x - \left( {m + 3} \right)} \right).\cos x = 0\]
\[ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{4{{\cos }^2}x + 4\cos x - \left( {m + 3} \right) = 0{\mkern 1mu} {\mkern 1mu} (1)}\\{\cos x = 0{\mkern 1mu} {\mkern 1mu} (2)}\end{array}} \right.\]
Phương trình \[(2) \Leftrightarrow x = \frac{\pi }{2} + k\pi {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \left( {k \in Z} \right)\]. Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2}}\\{x = \frac{{3\pi }}{2}}\end{array}} \right.\]
Thay \[\cos x = 0\] vào (1): \[{4.0^2} + 4.0 - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\]
+) Với \[m = - 3\]:
Phương trình \[(1) \Leftrightarrow 4{\cos ^2}x + 4\cos x = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{\cos x = 0}\\{\cos x = - 1}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = \frac{\pi }{2} + k\pi }\\{x = \pi + k2\pi }\end{array}} \right.{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} ,k \in \mathbb{Z}\]
Mà \[x \in \left( { - \frac{\pi }{2};2\pi } \right] \Rightarrow x \in \left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\}\]
Phương trình \[(*)\] có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] là \[\left\{ {\frac{\pi }{2};\frac{{3\pi }}{2};\pi } \right\} \Rightarrow m = - 3\] không thỏa mãn
+) Với \[m \ne - 3\]: Phương trình (1) không có nghiệm \[x = \frac{\pi }{2},{\mkern 1mu} {\mkern 1mu} x = \frac{{3\pi }}{2}\]. Khi đó, để (*) có đúng 5 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\] thì phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]
Đặt \[\cos x = t\], (1) trở thành: \[4{t^2} + 4t - \left( {m + 3} \right) = 0\] (3)
Phương trình (1) có đúng 3 nghiệm thuộc \[\left( { - \frac{\pi }{2};2\pi } \right]\]⇔ Phương trình (3) có 2 nghiệm \[{t_1},{\mkern 1mu} {\mkern 1mu} {t_2}{\mkern 1mu} {\mkern 1mu} \left( {{t_1} \le {t_2}} \right)\] thỏa mãn:
hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\], hoặc \[{t_1} = {t_2} \in \left( {0;1} \right)\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right.\], hoặc \[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right.\]
TH1: \[\left\{ {\begin{array}{*{20}{l}}{{t_1} = - 1}\\{{t_2} \in \left( { - 1;0} \right] \cup \left\{ 1 \right\}}\end{array}} \right.\]
\[ \Rightarrow 4.{\left( { - 1} \right)^2} + 4.\left( { - 1} \right) - \left( {m + 3} \right) = 0 \Leftrightarrow m = - 3\] (loại)
TH2: \[{t_1} = {t_2} \in \left( {0;1} \right)\]
\[ \Rightarrow \Delta ' = 0 \Leftrightarrow 4 + 4\left( {m + 3} \right) \Leftrightarrow 4m + 16 = 0 \Leftrightarrow m = - 4\]
Khi đó, (3) có 2 nghiệm \[{t_1} = {t_2} = - \frac{1}{2} \notin \left( {0;1} \right){\mkern 1mu} {\mkern 1mu} \Rightarrow m = - 4\]: không thỏa mãn
TH3:
\[\left\{ {\begin{array}{*{20}{l}}{{t_1} \in \left( {0;1} \right)}\\{{t_2} > 1}\end{array}} \right. \Leftrightarrow 0 < {t_1} < 1 < {t_2} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} > 0}\\{{t_1} + {t_2} > 0}\\{{t_1}{t_2} - \left( {{t_1} + {t_2}} \right) + 1 < 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} > 0}\\{ - \frac{4}{4} > 0}\\{1 - \left( { - \frac{4}{4}} \right) - \frac{{m + 3}}{4} < 0}\end{array}} \right. \Leftrightarrow m \in \emptyset \]
TH4:
\[\left\{ {\begin{array}{*{20}{l}}{{t_1} < - 1}\\{{t_2} \in \left( {0;1} \right)}\end{array}} \right. \Leftrightarrow {t_1} < - 1 < 0 < {t_2} < 1 \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{\Delta ' > 0}\\{{t_1}{t_2} < 0}\\{\left( {{t_1} + 1} \right)\left( {{t_2} + 1} \right) < 0}\\{\left( {{t_1} - 1} \right) + \left( {{t_2} - 1} \right) < 0}\\{\left( {{t_1} - 1} \right)\left( {{t_2} - 1} \right) > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{4m + 16 > 0}\\{ - \frac{{m + 3}}{4} < 0}\\{ - \frac{{m + 3}}{4} + \left( { - \frac{4}{4}} \right) + 1 < 0}\\{ - \frac{4}{4} - 2 < 0}\\{ - \frac{{m + 3}}{4} - \left( { - \frac{4}{4}} \right) + 1 > 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{m > - 4}\\{m > - 3}\\{m < 5}\end{array}} \right. \Leftrightarrow m \in \left( { - 3;5} \right)\]
Vậy, tập các giá trị thực của m thỏa mãn yêu cầu đề bài là: \[S = \left( { - 3;5} \right)\]
