Câu hỏi:
03/04/2024 51
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm các cạnh SA và SD.
1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
Cho hình chóp S.ABCD có đáy là hình bình hành ABCD với O là giao điểm hai đường chéo AC và BD. Gọi M, N lần lượt là trung điểm các cạnh SA và SD.
1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
Trả lời:
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
1. Sử dụng định lí \(\left\{ \begin{array}{l}d \not\subset \left( P \right)\\a \subset \left( P \right)\\d//a\end{array} \right. \Rightarrow d//\left( P \right)\) để chứng minh đường thẳng song song mặt phẳng.
Sử dụng định lí \(\left\{ \begin{array}{l}a,b \subset \left( P \right),a'b' \subset \left( Q \right)\\a \cap b = I,a' \cap b' = I'\\a//a',b//b'\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\) để chứng minh hai mặt phẳng song song.
2. Sử dụng định lí \(\left\{ \begin{array}{l}d \subset \left( P \right)\\\left( P \right)//\left( Q \right)\end{array} \right. \Rightarrow d//\left( Q \right)\) để chứng minh đường thẳng song song mặt phẳng.
3. Xác định các giao tuyến của mặt phẳng đã cho với các mặt của hình chóp và suy ra thiết diện.
Cách giải:
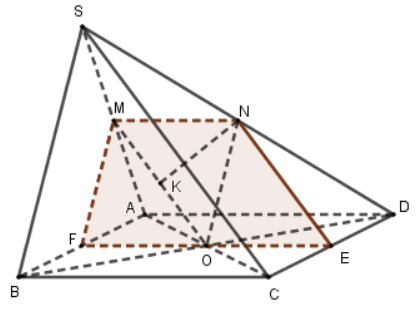
1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
Ta có: MO là đường trung bình của tam giác SAC nên \(MO//SC\).
Mà \(SC \subset \left( {SBC} \right)\) nên \(MO//\left( {SBC} \right)\).
MN là đường trung bình của \(\Delta SAD\) nên \(MN//AD\), mà \(AD//BC\) nên \(MN//BC\).
Ta có: \(\left\{ \begin{array}{l}MN,MO \subset \left( {OMN} \right)\\BC,SC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow \left( {OMN} \right)//\left( {SBC} \right)\)
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
Dễ thấy \(NK \subset \left( {OMN} \right)\).
Mà \(\left( {OMN} \right)//\left( {SBC} \right)\) nên \(NK//\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
Ta có:
\(BC \subset \left( {SBC} \right)//\left( {OMN} \right)\) nên \(BC//\left( {OMN} \right)\)
Mà \(BC \subset \left( {ABCD} \right)\) nên \(\left( {OMN} \right) \cap \left( {ABCD} \right) = Ox//BC\).
Trong \(\left( {ABCD} \right)\), qua O kẻ đường thẳng song song với BC cắt CD, AB lần lượt tại E, F.
Khi đó,
\(\left( {OMN} \right) \cap \left( {ABCD} \right) = EF\)
\(\left( {OMN} \right) \cap \left( {SAB} \right) = FM\)
\[\left( {OMN} \right) \cap \left( {SAD} \right) = MN\]
\[\left( {OMN} \right) \cap \left( {SCD} \right) = NE\]
\( \Rightarrow \) Thiết diện là tứ giác MNEF.
Mà \(MN//BC\), \(EF//BC\) nên \(MN//EF\) hay thiết diện là hình thang MNEF.
Phương pháp:
1. Sử dụng định lí \(\left\{ \begin{array}{l}d \not\subset \left( P \right)\\a \subset \left( P \right)\\d//a\end{array} \right. \Rightarrow d//\left( P \right)\) để chứng minh đường thẳng song song mặt phẳng.
Sử dụng định lí \(\left\{ \begin{array}{l}a,b \subset \left( P \right),a'b' \subset \left( Q \right)\\a \cap b = I,a' \cap b' = I'\\a//a',b//b'\end{array} \right. \Rightarrow \left( P \right)//\left( Q \right)\) để chứng minh hai mặt phẳng song song.
2. Sử dụng định lí \(\left\{ \begin{array}{l}d \subset \left( P \right)\\\left( P \right)//\left( Q \right)\end{array} \right. \Rightarrow d//\left( Q \right)\) để chứng minh đường thẳng song song mặt phẳng.
3. Xác định các giao tuyến của mặt phẳng đã cho với các mặt của hình chóp và suy ra thiết diện.
Cách giải:

1. Chứng minh MO song song với mặt phẳng \(\left( {SBC} \right)\) và mặt phẳng \(\left( {OMN} \right)\) song song với mặt phẳng \(\left( {SBC} \right)\).
Ta có: MO là đường trung bình của tam giác SAC nên \(MO//SC\).
Mà \(SC \subset \left( {SBC} \right)\) nên \(MO//\left( {SBC} \right)\).
MN là đường trung bình của \(\Delta SAD\) nên \(MN//AD\), mà \(AD//BC\) nên \(MN//BC\).
Ta có: \(\left\{ \begin{array}{l}MN,MO \subset \left( {OMN} \right)\\BC,SC \subset \left( {SBC} \right)\end{array} \right. \Rightarrow \left( {OMN} \right)//\left( {SBC} \right)\)
2. Gọi K là trung điểm của MO. Chứng minh rằng NK song song với \(\left( {SBC} \right)\).
Dễ thấy \(NK \subset \left( {OMN} \right)\).
Mà \(\left( {OMN} \right)//\left( {SBC} \right)\) nên \(NK//\left( {SBC} \right)\).
3. Xác định thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng \(\left( {OMN} \right)\). Hỏi thiết diện là hình gì?
Ta có:
\(BC \subset \left( {SBC} \right)//\left( {OMN} \right)\) nên \(BC//\left( {OMN} \right)\)
Mà \(BC \subset \left( {ABCD} \right)\) nên \(\left( {OMN} \right) \cap \left( {ABCD} \right) = Ox//BC\).
Trong \(\left( {ABCD} \right)\), qua O kẻ đường thẳng song song với BC cắt CD, AB lần lượt tại E, F.
Khi đó,
\(\left( {OMN} \right) \cap \left( {ABCD} \right) = EF\)
\(\left( {OMN} \right) \cap \left( {SAB} \right) = FM\)
\[\left( {OMN} \right) \cap \left( {SAD} \right) = MN\]
\[\left( {OMN} \right) \cap \left( {SCD} \right) = NE\]
\( \Rightarrow \) Thiết diện là tứ giác MNEF.
Mà \(MN//BC\), \(EF//BC\) nên \(MN//EF\) hay thiết diện là hình thang MNEF.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho hai đường thẳng phân biệt a, b và mặt phẳng \(\left( \alpha \right)\). Giả sử \(a//\left( \alpha \right)\), \(b \subset \left( \alpha \right)\). Khi đó:
Câu 2:
2. Trong trận bóng đá chung kết, hai bạn Việt và Nam tham gia sút phạt, biết rằng khả năng sút phạt vào lưới của Việt và Nam lần lượt là 0,7 và 0,8. Tính xác suất để ít nhất một bạn ghi bàn.
Câu 3:
Một hộp có 6 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng. Chọn ngẫu nhiên 5 viên bi trong hộp, tính xác suất để 5 viên bi được chọn có đủ ba màu và số bi xanh bằng số bi vàng.
Câu 4:
1. Trong một nhóm học sinh khối 11 tham gia hoạt động thiện nguyện gồm 3 học sinh nữ và 7 học sinh nam. Cần chọn ra 5 học sinh tham gia trong đợt thứ nhất. Tính xác suất để 5 học sinh được chọn không có quá 1 học sinh nữ.
1. Trong một nhóm học sinh khối 11 tham gia hoạt động thiện nguyện gồm 3 học sinh nữ và 7 học sinh nam. Cần chọn ra 5 học sinh tham gia trong đợt thứ nhất. Tính xác suất để 5 học sinh được chọn không có quá 1 học sinh nữ.


