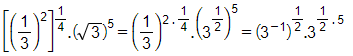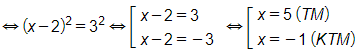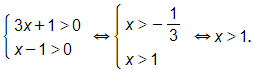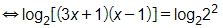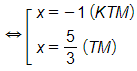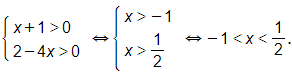Giải Toán 11 Bài tập cuối chương 6
Câu hỏi trắc nghiệm
Bài 1 trang 34 Toán 11 Tập 2: Rút gọn biểu thức 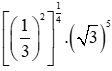
A. √3.
B. 3√3.
C. 1√3.
D. 9.
Lời giải:
Đáp án đúng là: D
=3− 12 . 352=3− 12+52=32=9.
Bài 2 trang 34 Toán 11 Tập 2: Nếu 2α = 9 thì (116)α8 có giá trị bằng
A. 13.
B. 3.
C. 19.
D. 1√3.
Lời giải:
Đáp án đúng là: A
(116)α8=(2− 4)α8=2− 4 . α8=2− 12α
=(2α)− 12=9− 12=13.
Bài 3 trang 34 Toán 11 Tập 2: Nếu a12=b (a>0 , a≠1) thì
A. log12a=b.
B. 2logab=1.
C. loga12=b.
D. log12b=a.
Lời giải:
Đáp án đúng là: B
a12=b⇔logab=12⇔2logab=1.
Bài 4 trang 34 Toán 11 Tập 2: Nếu x=log34+log94 thì 3x có giá trị bằng
A. 6.
B. 8.
C. 16.
D. 64.
Lời giải:
Đáp án đúng là: B
Ta có x=log34+log94=log34+log324
=log34+12log34=log34+log3412
=log34+12log34=log34+log32
=log3(4 . 2)=log38
⇔ 3x = 8.
Bài 5 trang 34 Toán 11 Tập 2: Cho α, β là hai số thực với α < β. Khẳng định nào sau đây đúng ?
A. (0,3)α<(0,3)β.
B. πα≥πβ.
C. (√2)α<(√2)β.
D. (12)β>(12)α.
Lời giải:
Đáp án đúng là: C
• Xét phương án A.
Do 0 < 0,3 < 1 nên hàm số y = 0,3x nghịch biến trên ℝ.
Mà α < β nên (0,3)α < (0,3)β.
• Xét phương án B.
Do π > 1 nên hàm số y = πx đồng biến trên ℝ.
Mà α < β nên πα < πβ.
• Xét phương án C.
Do √2>1 nên hàm số y=(√2)x đồng biến trên ℝ.
Mà α < β nên (√2)α<(√2)β.
• Xét phương án D.
Do 0<12<1 nên hàm số y=(12)x đồng biến trên ℝ.
Mà α < β nên(12)α<(12)β⇔(12)β>(12)α.
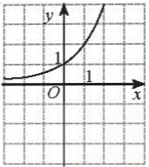
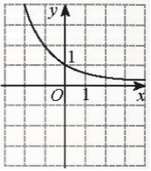
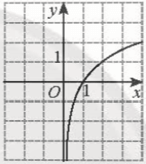
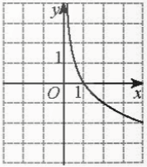
Bài 6 trang 34 Toán 11 Tập 2: Hình nào vẽ đồ thị của hàm số y=log12x?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: D
− Hàm số y=log12xnghịch biến trên (0; +∞). Loại A, C.
− Giới hạn: limx→+∞log12x=−∞; limx→0+log12x=+∞. Loại B.
Bài 7 trang 34 Toán 11 Tập 2: Phương trình 0,12x−1=100 có nghiệm là
A. −12.
B. 13.
C. 112.
D. 213.
Lời giải:
Đáp án đúng là: A
0,12x−1=100⇔0,12x−1=0,1−2⇔2x−1=−2
⇔2x=−1⇔x=−12.
Bài 8 trang 34 Toán 11 Tập 2: Tập nghiệm của bất phương trình 0,53x1>0,25 là
A. (−∞; 1).
B. (1; +∞).
C. (0; 1).
D. (−∞ ; −13).
Lời giải:
Đáp án đúng là: A
0,53x−1>0,25⇔0,53x−1>0,52
⇔3x−1<2(do 0<0,5<1)
⇔3x<3⇔x<1.
Vậy tập nghiệm của bất phương trình là (−∞;1).
Bài 9 trang 34 Toán 11 Tập 2: Nếu logx=2log5−log2 thì
A. x = 8.
B. x = 23.
C. x = 12,5.
D. x = 5.
Lời giải:
Đáp án đúng là: C
ĐKXĐ: x > 0
Khi đó: logx=2log5−log2⇔logx=log52−log2
⇔logx=log252⇔x=252=12,5.
Bài 10 trang 34 Toán 11 Tập 2: Số nguyên dương nhỏ nhất thỏa mãn log0,1(1−2x)>−1 là
A. x = 0.
B. x = 1.
C. x = −5.
D. x = −4.
Lời giải:
Đáp án đúng là: D
ĐKXĐ: 1−2x>0⇔x<12.
Khi đó: log0,1(1−2x)>−1⇔1−2x<0,1−1
⇔1−2x<10⇔−2x<9⇔x>−92.
Kết hợp với điều kiện ta được nghiệm của bất phương trình là −92<x<12.
Vậy số nguyên x nhỏ nhất thỏa mãn log0,1(1−2x)>−1 là x = − 4.
Bài tập tự luận
Bài 11 trang 35 Toán 11 Tập 2: Biết 4α + 4−α = 5. Tính giá trị biểu thức :
Lời giải:
a) Ta có (2α+2−α)2=(2α)2+2 . 2α . 2−α+(2−α)2
=(22)α+2+(22)−α=4α+2+4−α
=(4α+4−α)+2=5+2=7.
Vậy 2α+2−α=√7.
b) Ta có 42α+4−2α=(4α)2+(4−α)2
=(4α)2+2 . 4α . 4−α+(4−α)2−2 . 4α . 4−α
=(4α+4−α)2−2=52−2=23.
Vậy 42α+4−2α=23.
Bài 12 trang 35 Toán 11 Tập 2: Tính giá trị của biểu thức :
Lời giải:
a )log272−12(log23+log227)=log272−12log2(3 . 27)
=log272−12log281=log272−log28112
=log272−log29=log2729=log28
=log223=3log22=3;
b) 5log240 − log25=5log2405=5log28=5log223
=53log22=53=125;
c) 32 + log92=3log992+ log92=3log9(92 . 2)=3log32(92 . 2)
=312log3(92 . 2)=(3log3(92 . 2))12=(92 . 2)12=9√2.
Lời giải:
Ta có 5x = 3 ⇔ x = log5 3 và 3y = 5 ⇔ y = log3 5.
Do đó xy=log53 . log35=log53 . 1log53=1.
Bài 14 trang 35 Toán 11 Tập 2: Viết công thức biểu thị y theo x, biết
Lời giải:
Ta có 2log2y=2+12log2x
⇔log2y2=log222+log2x12
⇔log2y2=log2(22 . x12)
⇔y2=22 . x12⇔y=24√x.
Bài 15 trang 35 Toán 11 Tập 2: Giải các phương trình sau:
Lời giải:
a)(14)x−2=√8⇔((12)2)x−2=812
⇔(12)2(x−2)=((12)−3)12⇔(12)2x−4=(12)−32
⇔2x−4=−32⇔2x=52⇔x=54.
Vậy phương trình đã cho có nghiệm x=54.
b)92x−1=81 . 27x⇔(32)2x−1=34 . (33)x
⇔34x−2=33x+4⇔4x−2=3x+4
⇔4x−2=3x+4⇔4x−3x=2+4⇔x=6
Vậy phương trình đã cho có nghiệm x = 6.
c) ĐKXĐ: x – 2 > 0 ⇔ x > 2.
Khi đó: 2log5(x−2)=log59⇔log5(x−2)2=log532
Vậy phương trình đã cho có nghiệm x = 5.
d)ĐKXĐ:
Khi đó: log2(3x+1)=2−log2(x−1)
⇔log2(3x+1)+log2(x−1)=2
⇔log2(3x2−2x−1)=log24
⇔3x2−2x−1=4⇔3x2−2x−5=0
Vậy phương trình đã cho có nghiệm x=53.
Bài 16 trang 35 Toán 11 Tập 2: Giải các bất phương trình :
Lời giải:
a)(19)x+1>181⇔(19)x+1>(19)2
⇔x+1<2(do 0<19<1)
⇔x<1
Vậy bất phương trình đã cho có nghiệm x < 1.
b) (4√3)x≤27 . 3x⇔(314)x≤33 . 3x
⇔3x4≤33+x⇔x4≤3+x(do 3 > 1)
⇔x≥− 4.
Vậy bất phương trình đã cho có nghiệm x≥− 4.
c)ĐKXĐ:
Khi đó: log2(x+1)≤log2(2−4x)
⇔x+1≤2−4x⇔5x≤1⇔x≤15.
Kết hợp với điều kiện ta được nghiệm của bất phương trình −1<x≤15.
b) Sau 5 ngày thì số lượng vi khuẩn bằng bao nhiêu? Làm tròn kết quả đến hàng trăm.
Lời giải:
a) Ban đầu có 1000 vi khuẩn nên P0=1000.
Sau 2 ngày, số lượng vi khuẩn là:
P=125% . P0=125%.1000=1250
Ta có:P(2)=P0.a2⇔1250=1000.a2
⇔a2=1,25⇔a≈1,12.
b) Số lượng vi khuẩn sau 5 ngày là:
P(5)=P0.a5=1000.1,122≈1800(vi khuẩn).
c) Với P(t)=2P0, ta có:
P(t)=P0.at⇔2P0=P0.1,12t
⇔1,12t=2⇔t=log1,122≈6,1(ngày)
Vậy sau 6,1 ngày thì số lượng vi khuẩn vượt gấp đôi số lượng ban đầu.
Lời giải:
a)• pHA=1,9⇔−log[H+]=1,9
⇔log[H+]=−1,9⇔H+=10−1,9.
Vậy độ acid của dung dịch A là 10−1,9 mol/L.
• pHB=2,5⇔−log[H+]=2,5
⇔log[H+]=−2,5⇔H+=10−2,5.
Vậy độ acid của dung dịch B là 10−2,5mol/L.
Ta có: 10−1,910−2,5≈3,98.
Vậy độ acid của dung dịch A cao hơn độ acid của dung dịch B 3,98 lần.
b) Ta có:6,5
⇔−6,5>log[H+]>−6,7⇔10−6,5>H+>10−6,7.
Do đó nước chảy từ vòi nước có độ acid từ 10−6,7mol/L đến 10−6,5mol/L.
Vậy nước đó có độ acid cao hơn nước cất.
Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: