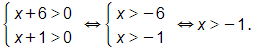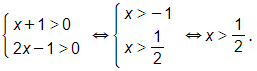Giải SGK Toán 11 (Chân trời sáng tạo) Bài 4: Phương trình, bất phương trình mũ và lôgarit

Giải Toán 11 Bài 4: Phương trình, bất phương trình mũ và lôgarit

Hoạt động khởi động trang 26 Toán 11 Tập 2: Sau khi sinh vật chết, lượng đồng vị phóng xạ carbon-14 trong cơ thể cứ sau 5730 năm thì giảm đi một nửa do quá trình phân rã. Đây là cơ sở của phương pháp xác định tuổi của hoá thạch bằng carbon phóng xạ carbon-14 trong khảo cố học.

(Nguồn:https://www.britannica.com/science/carbon-14)

Việc tính toán tuổi của hoá thạch được thực hiện như thế nào?

Lời giải:

Lượng carbon-14 trong hóa thạch được tính theo công thức $M=M_0.{\left(\frac{1}{2}\right)}^{\frac{t}{5730}}$, trong đó M₀ là lượng carbon-14 có trong cơ thể sinh vật khi chết, t là thời gian tính theo năm kể từ khi sinh vật chết đến khi khảo sát. Từ đây, nếu biết M và M₀ thì tìm được t.

1. Phương trình mũ

Hoạt động khám phá 1 trang 26 Toán 11 Tập 2: Số lượng cá thể vi khuẩn của một mẻ nuôi cấy tuân theo công thức P(t) = 50 . 10^kt, trong đó t là thời gian tính bằng giờ kể từ thời điểm bắt đầu nuôi cấy, k là hằng số.

(Nguồn: Sinh học 10, NXB Giáo dục Việt Nam, năm 2017, trang 101)

a) Ban đầu mẻ có bao nhiêu cá thể vi khuẩn?

b) Sau 1 giờ thì mẻ có 100 cá thể vi khuẩn. Tìm giá trị của k (làm tròn kết quả đến hàng phần mười).

c) Sau bao lâu thì số lượng cá thể vi khuẩn đạt đến 50000?

Lời giải:

a) Số cá thể vi khuẩn ban đầu mẻ có là:

P(0)=50.10^k.0=50.10⁰=50 (cá thể)

Vậy ban đầu mẻ có 50 cá thể vi khuẩn.

b) Với t=1,P(t)=100ta có:

P(1)=50.10^k.1⇔100=50.10^k⇔10^k=2⇔k=log2≈0,3.

Vậy k≈0,3.

c) Thời gian để số lượng cá thể vi khuẩn đạt đến 50000 là:

50000=50.10^0,3t⇔10^0,3t=1000

⇔0,3t=log1000⇔0,3t=3⇔t=10(giờ)

Vậy sau 10 giờ thì số lượng cá thể vi khuẩn đạt đến 50000.

Hoạt động khám phá 2 trang 27 Toán 11 Tập 2: Cho đồ thị của hai hàm số y = a^x và y = b như Hình 2a (với a > 0) hay Hình 2b (với 0 < a < 1). Từ đây, hãy nhận xét về số nghiệm và công thức nghiệm của phương trình a^x = b trong hai trường hợp b < 0 và b ≤ 0.

Lời giải:

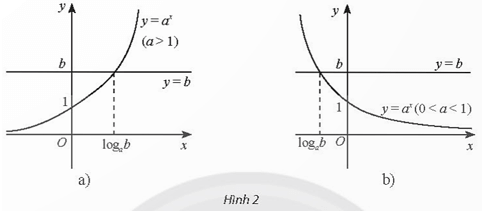
•Khi b>0, đồ thị của hai hàm số y=ax và y=b cắt nhau tại một điểm duy nhất.

Khi đó, phương trình ax=b có nghiệm duy nhất x=log_ab.

•Khi b≤0, đồ thị của hai hàm số y=ax và y=b không có điểm chung.

Khi đó, phương trình ax=b vô nghiệm.

Thực hành 1 trang 28 Toán 11 Tập 2: Giải các phương trình sau:

a) $3^{x+2}=\sqrt[3]{9}$;

b) 2.10^2x = 30;

c) 4^2x = 8^{2x – 1}.

Lời giải:

a) $3^{x+2}=\sqrt[3]{9}\iff 3^{x+2}=9^{\frac{1}{3}}\iff 3^{x+2}={\left(3^2\right)}^{\frac{1}{3}}$

$\iff 3^{x+2}=3^{\frac{2}{3}}\iff x+2=\frac{2}{3}\iff x=-\frac{4}{3}$;

b) $2.{10}^{2x}=30\iff {10}^{2x}=15\iff 2x=\log 15\iff x=\frac{1}{2}\log 15$;

c) $4^{2x}=8^{2x-1}\iff 2^{2.2x}=2^{3\left(2x-1\right)}\iff 2^{4x}=2^{6x-3}$

$\iff 4x=6x-3\iff 2x=3\iff x=\frac{3}{2}$.

Vận dụng 1 trang 28 Toán 11 Tập 2: Công thức tính khối lượng còn lại của một chất phóng xạ từ khối lượng ban đầu M₀ là $M\left(t\right)=M_0{\left(\frac{1}{2}\right)}^{\frac{t}{T}}$, trong đó t là thời gian tính từ thời điểm ban đầu và T là chu kỳ bán rã của chất. Đồng vị plutonium-234 có chu kỳ bán rã là 9 giờ.

(Nguồn: https://pubchem.ncbi.nlm.nih.gov/elemene/Plutonium#section=Atomic-

Mass-Half-Life-and-Decay)

Từ khối lượng ban đầu 200 g, sau bao lâu thì khối lượng plutonium-234 còn lại là:

a) 100 g? b) 50 g? c) 20 g?

Lời giải:

a) Với M₀ = 200, T = 9 , M(t) = 100, ta có:

$100=200{\left(\frac{1}{2}\right)}^{\frac{t}{9}}\iff {\left(\frac{1}{2}\right)}^{\frac{t}{9}}=\frac{1}{2}\iff \frac{t}{9}=1\iff t=9$.

Vậy sau 9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 100 g.

b) Với M₀ = 200, T = 9 , M(t) = 50, ta có:

$50=200{\left(\frac{1}{2}\right)}^{\frac{t}{9}}\iff {\left(\frac{1}{2}\right)}^{\frac{t}{9}}=\frac{1}{4}$

$\iff {\left(\frac{1}{2}\right)}^{\frac{t}{9}}={\left(\frac{1}{2}\right)}^2\iff \frac{t}{9}=2\iff t=18$

Vậy sau 18 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 50 g.

c) Với M₀ = 200, T = 9 , M(t) = 20, ta có:

$20=200{\left(\frac{1}{2}\right)}^{\frac{t}{9}}\iff {\left(\frac{1}{2}\right)}^{\frac{t}{9}}=\frac{1}{10}\iff \frac{t}{9}={\log }_{\frac{1}{2}}\frac{1}{10}$

$\iff \frac{t}{9}={\log }_{2}10\iff t=9{\log }_{2}10\approx \mathrm{29,9}$.

Vậy sau khoảng 29,9 giờ thì khối lượng plutonium-234 ban đầu 200 g còn lại là 20 g.

2. Phương trình lôgarit

Hoạt động khám phá 3 trang 28 Toán 11 Tập 2: Nhắc lại rằng, độ pH của một dung dịch tính theo công thức pH = −log x, trong đó x là nồng độ ion H⁺ tính bằng mol/L.

Biết sữa có độ pH là 6,5. Nồng độ H⁺ của sữa bằng bao nhiêu?

Lời giải:

Ta có pH = −log x ⇔ 6,5 = −log x

⇔ log x = −6,5 ⇔ x = 10^−6,5 ≈ 3,16.10⁻⁷.

Vậy nồng độ H⁺ của sữa bằng 3,16.10⁻⁷ mol/L.

Hoạt động khám phá 4 trang 29 Toán 11 Tập 2: Cho đồ thị của hàm số y = log_a x (a > 0, a ≠ 1) và y = b như Hình 3a (với a > 1) hay Hình 3b (với 0 < a < 1). Từ đây hãy nhận xét về số nghiệm và công thức nghiệm của phương trình ${\log }_{a}x=b$.

Lời giải:

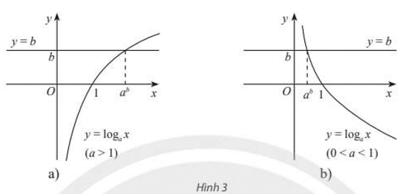
Đồ thị của hai hàm số y=log_ax và y=b luôn cắt nhau tại một điểm duy nhất.

Khi đó, phương trình log_ax=b có nghiệm duy nhất x=a^b.

Thực hành 2 trang 30 Toán 11 Tập 2: Giải phương trình sau:

a) ${\log }_{\frac{1}{2}}\left(x-2\right)=-2$;

b) ${\log }_2\left(x+6\right)={\log }_2\left(x+1\right)+1$.

Lời giải:

a) ${\log }_{\frac{1}{2}}\left(x-2\right)=-2$

Điều kiện x – 2 > 0 ⇔ x > 2.

Khi đó ${\log }_{\frac{1}{2}}\left(x-2\right)=-2\iff x-2={\left(\frac{1}{2}\right)}^{-2}$

$\iff x-2={\left(\frac{1}{2}\right)}^{-2}=4\iff x=2+4=6$ (TM)

Vậy phương trình đã cho có nghiệm là x = 6.

b) ${\log }_2\left(x+6\right)={\log }_2\left(x+1\right)+1$.

Điều kiện 

Khi đó ${\log }_2\left(x+6\right)={\log }_2\left(x+1\right)+1$

$\iff {\log }_2\left(x+6\right)-{\log }_2\left(x+1\right)=1$$\iff {\log }_2\left(\frac{x+6}{x+1}\right)=1$

$\iff \frac{x+6}{x+1}=2\iff x+6=2\left(x+1\right)$

$\iff x+6=2x+2\iff x=4$(TM).

Vậy phương trình đã cho có nghiệm là x = 4.

3. Bất phương trình mũ

Hoạt động khám phá 5 trang 30 Toán 11 Tập 2: Xét quần thể vi khuẩn ở Hoạt động khám phá 1.

a) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50 000?

b) Ở những thời điểm nào thì số lượng cá thể vi khuẩn vượt quá 50 000 nhưng chưa vượt quá 100 000?

Lời giải:

Do 10>1nên hàm số P(t)=50.10^kt đồng biến trên ℝ.

a) Tại thời điểm t=10 thì số lượng cá thể vi khuẩn bằng 50000.

Vì hàm số đồng biến trên ℝ nên với t>10 thì số lượng cá thể vi khuẩn vượt quá 50000.

b) Thời gian để số lượng cá thể vi khuẩn đạt đến 100000 là:

100000=50.10^0,3t⇔10^0,3t=2000

⇔0,3t=log2000⇔t≈11 (giờ)

•Tại thời điểm t=10 thì số lượng cá thể vi khuẩn bằng 50000.

•Tại thời điểm t=11 thì số lượng cá thể vi khuẩn bằng 100000.

Vì hàm số đồng biến trên ℝ nên với 10

Thực hành 3 trang 31 Toán 11 Tập 2: Giải các bất phương trình sau:

a)2^x > 16;

b) 0,1^x ≤ 0,001;

c) ${\left(\frac{1}{5}\right)}^{x-2}\ge {\left(\frac{1}{25}\right)}^x$.

Lời giải:

a) 2^x > 16 ⇔ 2^x > 2⁴ ⇔ x > 4 (do 2 > 1).

Vậy nghiệm của bất phương trình đã cho là x > 4.

b) 0,1^x ≤ 0,001 ⇔ 0,1^x ≤ 0,1³⇔ x ≥ 3 (do 0 < 0,1 < 1).

Vậy nghiệm của bất phương trình đã cho là x ≥ 3.

c) ${\left(\frac{1}{5}\right)}^{x-2}\ge {\left(\frac{1}{25}\right)}^x\iff {\left(\frac{1}{5}\right)}^{x-2}\ge {\left({\left(\frac{1}{5}\right)}^2\right)}^x$

$\iff {\left(\frac{1}{5}\right)}^{x-2}\ge {\left(\frac{1}{5}\right)}^{2x}\iff x-2\le 2x$ (do $0<\frac{1}{5}<1$).

$\iff x\ge -2$.

Vậy nghiệm của bất phương trình đã cho là x ≥ −2.

4. Bất phương trình lôgarit

Hoạt động khám phá 6 trang 31 Toán 11 Tập 2: Biết rằng máu của người bình thường có độ pH từ 7,3 đến 7,45 (nguồn: Hóa học 11, NXB Giáo dục Việt Nam, năm 2017, trang 15). Nồng độ H⁺trong máu nhận giá trị trong miền nào?

Lời giải:

Ta có $pH=-\log x={\log }_{{10}^{-1}}x={\log }_{\frac{1}{10}}x$.

Do $0<\frac{1}{10}<1$nên hàm số $pH={\log }_{\frac{1}{10}}x$nghịch biến trên (0; +∞).

Độ pH từ 7,3 đến 7,45 hay 7,3 ≤ −log x ≤7,45

⇔ −7,3 ≥ log x ≥ −7,45⇔ 10^−7,3 ≥ x ≥ 10^−7,45.

Vì hàm số nghịch biến trên (0; +∞) nên nồng độ H⁺trong máu nhận giá trị trong miền từ 10^−7,45 mol/L đến 10^−7,3mol/L.

Thực hành 4 trang 32 Toán 11 Tập 2: Giải các bất phương trình sau:

a)${\log }_{\frac{1}{3}}\left(x+1\right)<2$;

b) ${\log }_5\left(x+2\right)\le 1$.

Lời giải:

a)${\log }_{\frac{1}{3}}\left(x+1\right)<2$

Điều kiện: x + 1 > 0 ⇔ x > −1.

${\log }_{\frac{1}{3}}\left(x+1\right)<2\iff x+1>{\left(\frac{1}{3}\right)}^2\iff x+1>\frac{1}{9}$

$\iff x>-1+\frac{1}{9}\iff x>-\frac{8}{9}$.

Vậy nghiệm của bất phương trình đã cho là $x>-\frac{8}{9}$.

b) ${\log }_5\left(x+2\right)\le 1$

Điều kiện: x + 2 > 0 ⇔ x > −2.

${\log }_5\left(x+2\right)\le 1\iff x+2\le 5\iff x\le 3$.

Kết hợp với điều kiện, ta được nghiệm của bất phương trình đã cho là −2 < x ≤ 3.

Vận dụng 2 trang 32 Toán 11 Tập 2: Nước uống đạt tiêu chuẩn có độ pH nằm trong khoảng từ 6,5 đến 8,5 (theo Quy chuẩn Việt Nam QCVN 01:2009/BYT). Nồng độ H⁺ trong nước uống tiêu chuẩn phải nằm trong khoảng nào?

Lời giải:

Ta có 6,5 ≤ pH ≤ 8,5 ⇔6,5 ≤ −log x ≤ 8,5

⇔−6,5 ≥ log x ≥ 8,5 ⇔ 10^−6,5 ≥ x ≥ 10^−8,5.

Vậy nồng độ H⁺trong máu nhận giá trị trong miền từ 10^−8,5 mol/L đến 10^−6,5mol/L.

Bài tập

Bài 1 trang 32 Toán 11 Tập 2: Giải các phương trình sau:

a) 5^{2x – 1} = 25;

b)3^{x + 1} = 9^{2x + 1};

c)10^{1 – 2x} = 100 000.

Lời giải:

a)$5^{2x-1}=25\iff 5^{2x-1}=5^2$$\iff 2x-1=2\iff x=\frac{3}{2}$.

Vậy nghiệm của phương trình đã cho là $x=\frac{3}{2}$.

b)3^{x + 1} = 9^{2x + 1} ⇔ 3^{x + 1} = 3^{2(2x + 1)}

⇔ x + 1 = 2(2x + 1) ⇔ x + 1 = 4x + 2

⇔ 3x = −1 ⇔ $x=-\frac{1}{3}$.

Vậy nghiệm của phương trình đã cho là $x=-\frac{1}{3}$.

c) 10^{1 – 2x} = 100 000 ⇔ 10^{1 – 2x} = 10⁵

⇔ 1 – 2x = 5 ⇔ 2x = – 4 ⇔ x = – 2.

Vậy nghiệm của phương trình đã cho là x = – 2.

Bài 2 trang 33 Toán 11 Tập 2: Giải các phương trình sau. Làm tròn kết quả đến hàng nghìn.

a) 3^{x + 2} = 7;

b) 3 . 10^{2x + 1} = 5.

Lời giải:

a) 3^{x + 2} = 7 ⇔ x + 3 = log₃ 7

⇔ x = –3 + log₃ 7 ⇔ x ≈ –0,229.

Vậy nghiệm của phương trình đã cho là x ≈ –0,229.

b) $3.{10}^{2x+1}=5\iff {10}^{2x+1}=\frac{5}{3}\iff 2x+1=\log \frac{5}{3}$

$\iff 2x=\log \frac{5}{3}-1\iff x=\frac{1}{2}\left(\log \frac{5}{3}-1\right)\iff x\approx -\mathrm{0,389}$.

Vậy nghiệm của phương trình đã cho là x ≈ –0,389.

Bài 3 trang 33 Toán 11 Tập 2: Giải các phương trình sau:

a) log₆ (4x + 4) = 2;

b) log₃ x – log₃ (x – 2) = 1.

Lời giải:

a) Điều kiện: 4x + 4 > 0 ⇔ x > –1

Khi đó: log₆ (4x + 4) = 2 ⇔ 4x + 4 = 6²

⇔ 4x + 4 = 36 ⇔ 4x = 32 ⇔ x = 8 (TMĐK)

Vậy nghiệm của phương trình đã cho là x = 8.

b) Điều kiện: .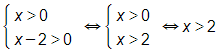

Khi đó: log₃ x – log₃ (x – 2) = 1

⇔ log₃ x – log₃ (x – 2) = 1

⇔ log₃ x = log₃ (x – 2) + 1

⇔ log₃ x = log₃ (x – 2) + log₃ 3

⇔ log₃ x = log₃ 3(x – 2)

⇔ x = 3(x – 2) ⇔ 2x = 6 ⇔ x = 3 (TMĐK)

Vậy nghiệm của phương trình đã cho là x = 3.

Bài 4 trang 33 Toán 11 Tập 2: Giải các bất phương trình sau:

a)${\left(\frac{1}{3}\right)}^{2x+1}\le 9$;

b) 4^x > 4^{x – 2}.

Lời giải:

a)${\left(\frac{1}{3}\right)}^{2x+1}\le 9\iff {\left(\frac{1}{3}\right)}^{2x+1}\le {\left(\frac{1}{3}\right)}^{-2}$

$\iff 2x+1\le -2$(do $0<\frac{1}{3}<1$)

$\iff 2x>-3\iff x>-\frac{3}{2}$.

Vậy nghiệm của bất phương trình là $x>-\frac{3}{2}$.

b)$4^x>4^{x-2}\iff {\left(2^2\right)}^x>4^{x-2}\iff 2^{2x}>4^{x-2}$

$\iff 2x>x-2$ (do 2 > 1)

⇔ x > – 2.

Vậy nghiệm của bất phương trình là x > – 2.

Bài 5 trang 33 Toán 11 Tập 2: Giải các bất phương trình sau:

a)log₂ (x – 2) < 2;

b)log (x + 1) ≥ log (2x – 1).

Lời giải:

a) Điều kiện: x – 2 > 0 ⇔ x > 2

Khi đó: log₂ (x – 2) < 2⇔ x – 2 < 2²

⇔ x – 2 < 4 ⇔ x < 6.

Kết hợp với điều kiện ta được nghiệm của bất phương trình là 2 < x < 6.

b)Điều kiện: 

Khi đó: log (x + 1) ≥ log (2x – 1)

⇔x + 1 ≥ 2x – 1 ⇔x ≥ –2⇔x ≤ 2.

Kết hợp với điều kiện ta được nghiệm của bất phương trình là $\frac{1}{2}<x\le 2$.

Bài 6 trang 33 Toán 11 Tập 2: Chất phóng xạ polonium-210 có chu kì bán rã là 138 ngày. Điều này có nghĩa là cứ sau 138 ngày, lượng polonium còn lại trong một mẫu chỉ bằng một nửa lượng ban đầu. Một mẫu 100g có khối lượng polonium-210 còn lại sau t ngày được tính theo công thức $M\left(t\right)=100{\left(\frac{1}{2}\right)}^{\frac{t}{138}}\left(g\right)$.

(nguồn://pubchem.ncbi.nlm.nih.gov/element/Polonium#section=

Atiomc-Mass-Half-Life-anh-Decay)

a) Khối lượng polonium-210 còn lại bao nhiêu sau 2 năm?

b) Sau bao lâu thì còn lại 40 g polonium-210.

Lời giải:

a) Sau 2 năm (tức t = 730), khối lượng polonium-210 còn lại là:

$M\left(730\right)=100{\left(\frac{1}{2}\right)}^{\frac{730}{138}}\approx \mathrm{1,92}\left(g\right)$.

Vậy khối lượng polonium-210 còn lại sau 2 năm khoảng 1,92 g.

b) Ta có $M\left(t\right)=40\iff 100{\left(\frac{1}{2}\right)}^{\frac{t}{138}}=40\iff {\left(\frac{1}{2}\right)}^{\frac{t}{138}}=\frac{2}{5}$

$\iff \frac{t}{138}={\log }_{\frac{1}{2}}\frac{2}{5}\iff t=138{\log }_{\frac{1}{2}}\frac{2}{5}\approx \mathrm{182,43.}$

Vậy sau khoảng 182,43 ngày thì còn lại 40 g polonium-210.

Bài 7 trang 33 Toán 11 Tập 2: Nhắc lại rằng, mức cường độ âm L được tính bằng công thức $L=\log \left(\frac{I}{I_0}\right)\left(dB\right)$, trong đó I là cường độ của âm tính bằng W/m2 và $I_0={10}^{12}\text{\hspace{0.17em}\hspace{0.17em}W}/m^2.$

(Nguồn: Vật lí 12, NXB Giáo dục Việt Nam, năm 2017, trang 52)

a) Một giáo viên đang giảng bài trong lớp học, có mức cường độ âm là 50 dB. Cường độ âm của giọng nói giáo viên bằng bao nhiêu?

b) Mức cường độ âm trong một nhà xưởng thay đổi trong khoảng từ 75 dB đến 90 dB. Cường độ âm trong nhà xưởng này thay đổi trong khoảng nào?

Lời giải:

a) Ta có $L=50\iff 10\log \left(\frac{I}{I_0}\right)=50\iff 10\log \left(\frac{I}{{10}^{-12}}\right)=50$

$\iff \log \left(\frac{I}{{10}^{-12}}\right)=5\iff \frac{I}{{10}^{-12}}={10}^5\iff I={10}^{-7}\left(W/m^2\right)$.

Vậy cường độ âm của giọng nói giáo viên bằng 10^–7 (W/m²).

b) Ta có $75\le L\le 90\iff 75\le 10\log \left(\frac{I}{I_0}\right)\le 90$

$\iff 75\le 10\log \left(\frac{I}{{10}^{-12}}\right)\le 90\iff \mathrm{7,5}\le \log \left(\frac{I}{{10}^{-12}}\right)\le 9$

$\iff {10}^{\mathrm{7,5}}\le \frac{I}{{10}^{-12}}\le {10}^9\iff {10}^{-\mathrm{4,5}}\le I\le {10}^{-3}\left(W/m^2\right)$.

Vậy cường độ âm trong nhà xưởng này thay đổi trong khoảng 10^–4,5 (W/m²) đến 10^–3 (W/m²).

Xem thêm các bài giải SGK Toán 11 Chân trời sáng tạo hay, chi tiết khác: