Giải SGK Toán 10 (Chân trời sáng tạo) Bài 4: Tích vô hướng của hai vectơ

Tổng quan

Hỏi đáp (14)

Chủ đề (7)

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 10 Bài 4: Tích vô hướng của hai vectơ sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 4. Mời các bạn đón xem:

Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ

1. Góc giữa hai vectơ

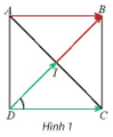
Hoạt động khám phá 1 trang 98 Toán lớp 10 Tập 1: Cho hình vuông ABCD có tâm I (Hình 1).

Cho hình vuông ABCD có tâm I (Hình 1). Tính góc IDC

a) Tính $\hat{I D C}$ .

b) Tìm hai vectơ cùng có điểm đầu là D và điểm cuối lần lượt là I và C.

c) Tìm hai vectơ cùng có điểm đầu là D và lần lượt bằng $\vec{I B}$ và $\vec{A B}$ .

Lời giải:

a) Hình vuông ABCD có tâm I nên IA = IB = IC = ID và AC $⊥$ BC tại I.

Do đó tam giác IDC vuông cân tại I.

Khi đó $\hat{I D C}$ = 45^o.

b) Vectơ có điểm đầu là D, điểm cuối là I là vectơ $\vec{D I}$ .

Vectơ có điểm đầu là D, điểm cuối là C là vectơ $\vec{D C}$ .

c) Vectơ có điểm đầu là D và bằng vectơ $\vec{I B}$ là vectơ $\vec{D I}$ .

Vectơ có điểm đầu là D và bằng vectơ $\vec{A B}$ là vectơ $\vec{D C}$ .

Thực hành 1 trang 99 Toán lớp 10 Tập 1: Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc: $(\vec{A B}, \vec{A C}), (\vec{A B}, \vec{B C}), (\vec{A H}, \vec{B C}), (\vec{B H}, \vec{B C})$ , $(\vec{H B}, \vec{B C})$ .

Lời giải:

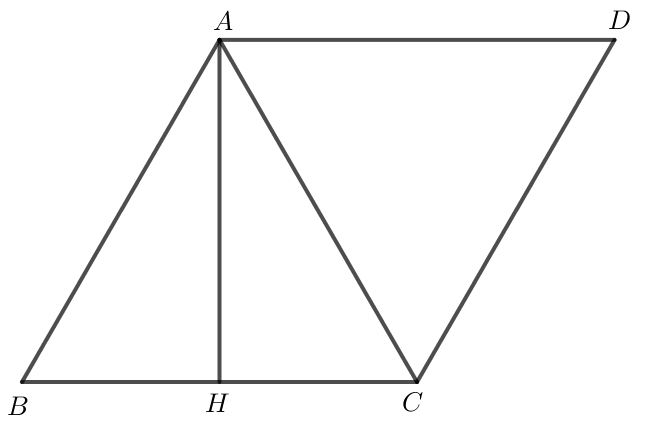
Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ - Chân trời sáng tạo (ảnh 1)

Dựng hình bình hành ABCD.

Do tam giác ABC đều nên $\hat{B A C}$ = 60^o, do đó $(\vec{A B}, \vec{A C})$ = 60^o.

Do ABCD là hình bình hành nên $\vec{B C} = \vec{A D}$ .

Do đó $(\vec{A B}, \vec{B C}) = (\vec{A B}, \vec{A D})$ .

Do ABCD là hình bình hành nên $\hat{A B C} + \hat{B A D} = 180 °$ .

Do đó $\hat{B A D} = 180 ° - \hat{A B C}$ = 180^o - 60^o = 120^o.

Khi đó $(\vec{A B}, \vec{A D})$ = 120^o hay $(\vec{A B}, \vec{B C})$ = 120^o.

Tam giác ABC đều có H là trung điểm của BC nên AH vừa là đường trung tuyến, vừa là đường cao trong tam giác ABC.

Do đó AH $⊥$ BC nên $(\vec{A H}, \vec{B C})$ = 90^o.

Hai vectơ $\vec{B H}$ và $\vec{B C}$ cùng hướng nên $(\vec{B H}, \vec{B C})$ = 0^o.

Hai vectơ $\vec{H B}$ và $\vec{B C}$ ngược hướng nên $(\vec{H B}, \vec{B C})$ = 180^o.

2. Tích vô hướng của hai vectơ

Hoạt động khám phá 2 trang 99 Toán lớp 10 Tập 1: Một người dùng một lực $\vec{F}$ kéo môt chiếc xe đi quãng đường dài 100 m. Tính công sinh bởi lực $\vec{F}$ , biết rằng góc giữa vectơ $\vec{F}$ và hướng di chuyển là 45°. (Công A (đơn vị: J) bằng tích của ba đại lượng: cường độ của lực $\vec{F}$ , độ dài quãng đường và côsin của góc giữa hai vectơ $\vec{F}$ và độ dịch chuyển $\vec{d}$ ).

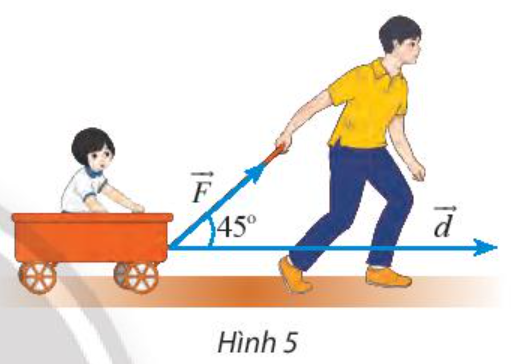
Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ - Chân trời sáng tạo (ảnh 1)

Lời giải:

Công sinh bởi lực $\vec{F}$ bằng:

$|\vec{F}| . |\vec{d}| . \cos (\vec{F}, \vec{d})$ = 10 . 100 . cos 45^o ≈ 707 J.

Vậy công sinh bởi lực $\vec{F}$ khoảng 707 J.

Thực hành 2 trang 100 Toán lớp 10 Tập 1: Cho tam giác ABC vuông cân tại A, cạnh huyền bằng $\sqrt{2}$ . Tính các tích vô hướng: $\vec{A B} . \vec{A C}, \vec{A C} . \vec{B C}, \vec{B A} . \vec{B C}$ .

Lời giải:

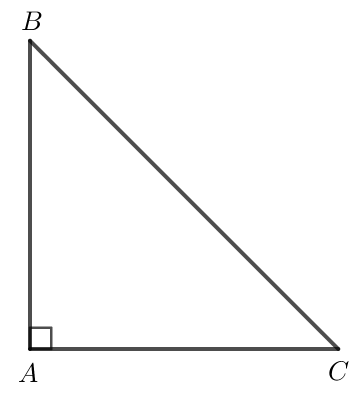
Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ - Chân trời sáng tạo (ảnh 1)

Do tam giác ABC vuông cân tại A nên AB $⊥$ AC.

Do đó $\vec{A B} ⊥ \vec{A C} \Rightarrow \vec{A B} . \vec{A C} = \vec{0}$ .

Áp dụng định lí Pythagore vào tam giác ABC vuông cân tại A ta có:

AB² + AC² = BC²

$\Rightarrow$ 2AB² = 2

$\Rightarrow$ AB² = 1

$\Rightarrow$ AB = 1 (do AB là độ dài đoạn thẳng nên AB > 0)

Tam giác vuông cân tại A nên $\hat{A B C} = \hat{A C B}$ = 45^o.

Ta có $\vec{A C} . \vec{B C} = - \vec{C A} . (- \vec{C B}) = \vec{C A} . \vec{C B}$ .

$\vec{C A} . \vec{C B} = |\vec{C A}| . |\vec{C B}| . \cos (\vec{C A} . \vec{C B})$ = 1 . $\sqrt{2}$ . cos $\hat{A C B}$ = 1 . $\sqrt{2}$ . cos 45^o = 1.

Do đó $\vec{A C} . \vec{B C}$ = 1.

$\vec{B A} . \vec{B C} = |\vec{B A}| . |\vec{B C}| . \cos (\vec{B A}, \vec{B C})$ = 1 . $\sqrt{2}$ . cos $\hat{A B C}$ = 1 . $\sqrt{2}$ . cos 45^o = 1.

Do đó $\vec{B A} . \vec{B C}$ = 1.

Thực hành 3 trang 100 Toán lớp 10 Tập 1: Hai vectơ $\vec{a}$ và $\vec{b}$ có độ dài lần lượt là 3 và 8 và có tích vô hướng là $12 \sqrt{2}$ . Tính góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ .

Lời giải:

Ta có $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b}) = 12 \sqrt{2}$

$\Rightarrow$ 3 . 8 . $\cos (\vec{a}, \vec{b}) = 12 \sqrt{2}$

$\Rightarrow \cos (\vec{a}, \vec{b}) = \frac{\sqrt{2}}{2}$

$\Rightarrow (\vec{a}, \vec{b})$ = 45^o.

Vậy góc giữa hai vectơ $\vec{a}$ và $\vec{b}$ bằng 45°.

Vận dụng 1 trang 100 Toán lớp 10 Tập 1: Một người dùng một lực $\vec{F}$ có độ lớn là 20 N kéo một vật dịch chuyển một đoạn 50 m cùng hướng với $\vec{F}$ . Tính công sinh bởi lực $\vec{F}$ .

Lời giải:

Do vật dịch chuyển cùng hướng với $\vec{F}$ nên góc tạo bởi vectơ hướng di chuyển của vật và $\vec{F}$ bằng 0^o.

Khi đó công sinh bởi lực $\vec{F}$ bằng:

20 . 50 . cos 0^o = 1 000 J.

Vậy công sinh bởi lực $\vec{F}$ bằng 1 000 J.

3. Tính chất của tích vô hướng

Thực hành 4 trang 101 Toán lớp 10 Tập 1: Cho hai vectơ $\vec{i}, \vec{j}$ vuông góc, cùng có độ dài bằng 1.

a) Tính: ${(\vec{i} + \vec{j})}^{2}; {(\vec{i} - \vec{j})}^{2}; (\vec{i} + \vec{j}) . (\vec{i} - \vec{j})$ .

b) Cho $\vec{a} = 2 \vec{i} + 2 \vec{j}, \vec{b} = 3 \vec{i} - 3 \vec{j}$ . Tính tích vô hướng $\vec{a} . \vec{b}$ và tính góc $(\vec{a}, \vec{b})$ .

Lời giải:

Do hai vectơ $\vec{i}, \vec{j}$ vuông góc nên $\vec{i} . \vec{j} = |\vec{i}| . |\vec{j}| c o s 90 ° = 0$ .

a) Ta có ${(\vec{i} + \vec{j})}^{2} = {\vec{i}}^{2} + 2 \vec{i} . \vec{j} + {\vec{j}}^{2} = {|\vec{i}|}^{2} + 2 |\vec{i}| . |\vec{j}| . c o s 90 ° + {|\vec{j}|}^{2}$ = 1² + 2 . 0 + 1² = 2.

${(\vec{i} - \vec{j})}^{2} = {\vec{i}}^{2} - 2 \vec{i} . \vec{j} + {\vec{j}}^{2} = {|\vec{i}|}^{2} - 2 |\vec{i}| . |\vec{j}| . c o s 90 ° + {|\vec{j}|}^{2}$ = 1² - 2 . 0 + 1² = 2.

$(\vec{i} + \vec{j}) . (\vec{i} - \vec{j}) = {\vec{i}}^{2} - {\vec{j}}^{2}$ = ${|\vec{i}|}^{2} - {|\vec{j}|}^{2}$ = 1² - 1² = 0.

b) $\vec{a} = 2 \vec{i} + 2 \vec{j} = 2 (\vec{i} + \vec{j})$ ; $\vec{b} = 3 \vec{i} - 3 \vec{j} = 3 (\vec{i} - \vec{j})$ .

Do đó $\vec{a} . \vec{b} = 2 (\vec{i} + \vec{j}) .3 (\vec{i} - \vec{j}) = 6 (\vec{i} + \vec{j}) (\vec{i} - \vec{j})$ = 6 . 0 = 0.

Khi đó cos $(\vec{a}, \vec{b})$ = $\frac{\vec{a} . \vec{b}}{|\vec{a}| . |\vec{b}|}$ = 0 (do $|\vec{a}|$ > 0 và $|\vec{b}|$ > 0).

$\Rightarrow (\vec{a}, \vec{b})$ = 90^o.

Vận dụng 2 trang 101 Toán lớp 10 Tập 1: Phân tử sulfur dioxide (SO₂) có cấu tạo hình chữ V, góc liên kết $\hat{O S O}$ gần bằng 120°. Người ta biểu diễn sự phân cực giữa nguyên tử S với mỗi nguyên tử O bằng các vectơ $\vec{μ_{1}}$ và $\vec{μ_{2}}$ có cùng phương với liên kết cộng hóa trị, có chiều từ nguyên tử S về mỗi nguyên tử O và cùng có độ dài là 1,6 đơn vị (Hình 6). Cho biết vectơ tổng $\vec{μ} = \vec{μ_{1}} + \vec{μ_{2}}$ được dùng để biểu diễn sự phân cực của cả phân tử SO₂. Tính độ dài của $\vec{μ}$ .

Phân tử sulfur dioxide (SO2) có cấu tạo hình chữ V, góc liên kết OSO gần bằng 120 độ

Lời giải:

Do $\vec{μ} = \vec{μ_{1}} + \vec{μ_{2}}$ nên $|\vec{μ}| = |\vec{μ_{1}} + \vec{μ_{2}}|$ .

Ta có ${|\vec{μ_{1}} + \vec{μ_{2}}|}^{2} = {(\vec{μ_{1}} + \vec{μ_{2}})}^{2} = {\vec{μ_{1}}}^{2} + 2 \vec{μ_{1}} . \vec{μ_{2}} + {\vec{μ_{2}}}^{2}$

$= 1, 6^{2} + 2 |\vec{μ_{1}}| . |\vec{μ_{2}}| . \cos (\vec{μ_{1}}, \vec{μ_{2}}) + 1, 6^{2}$

= 1,6² + 2 . 1,6 . 1,6 . cos 120^o + 1,6²

= 2,56

Do đó $|\vec{μ}| = |\vec{μ_{1}} + \vec{μ_{2}}| = \sqrt{2, 56}$ = 1,6.

Vậy độ dài của $\vec{μ}$ bằng 1,6 đơn vị.

Bài tập

Bài 1 trang 101 Toán lớp 10 Tập 1: Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng: $\vec{A B} . \vec{A D}$ , $\vec{A B} . \vec{A C}$ , $\vec{A C} . \vec{CB}$ , $\vec{A C} . \vec{BD}$ .

Lời giải:

Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng: vectơ AB . vectơAD, vectơ AB . vectơAC

AC là độ dài cạnh huyền của tam giác vuông cân có cạnh bằng a nên

AC = $\sqrt{a^{2} + a^{2}} = \sqrt{2} a$ .

Ta có ABCD là hình vuông nên AC = BD = $\sqrt{2} a$ .

Vì AB $⊥$ AD nên $\vec{A B} ⊥ \vec{A D}$ ⇒ $\vec{A B} . \vec{A D}$ = 0.

Tam giác ABC vuông cân tại B nên $\hat{B A C} = \hat{B C A}$ = 45^o.

$\vec{A B} . \vec{A C} = |\vec{A B}| . |\vec{A C}| . \cos (\vec{A B}, \vec{A C})$ = a . $\sqrt{2} a$ . cos $\hat{B A C}$ = $\sqrt{2}$ a² . cos 45^o = a².

Do đó $\vec{A B} . \vec{A C}$ = a².

$\vec{A C} . \vec{CB} = - \vec{C A} . \vec{CB} = - |\vec{C A}| . |\vec{C B}| . \cos (\vec{C A}, \vec{CB})$

= - $\sqrt{2} a$ . a . cos $\hat{B C A}$ = $- \sqrt{2}$ a² . cos 45^o = -a².

Do đó $\vec{A C} . \vec{CB}$ = -a².

Do ABCD là hình vuông nên AC $⊥$ BD.

Do đó $\vec{A C} ⊥ \vec{B D}$ nên $\vec{A C} . \vec{B D} =$ 0.

Bài 2 trang 101 Toán lớp 10 Tập 1: Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

a) $\vec{A B} . \vec{A O}$

b) $\vec{A B} . \vec{A D}$

Lời giải:

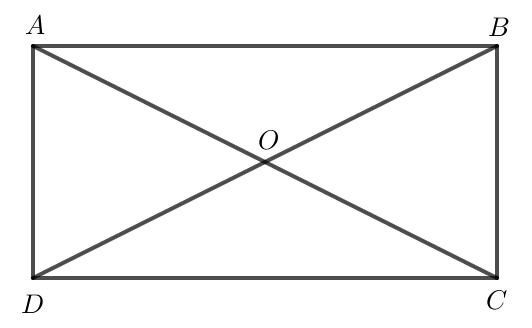
Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ - Chân trời sáng tạo (ảnh 1)

a) AC là độ dài cạnh huyền của tam giác vuông có độ dài hai cạnh lần lượt là 2a và a.

Do đó AC = $\sqrt{{(2 a)}^{2} + a^{2}} = \sqrt{5} a$ (do AC là độ dài đoạn thẳng nên AC > 0).

Hình chữ nhật ABCD có tâm O nên O là trung điểm của AC.

Do đó AO = $\frac{1}{2}$ AC = $\frac{\sqrt{5} a}{2}$ .

Tam giác ABC vuông tại B nên $cos \hat{B A C} = \frac{A B}{A C} = \frac{2 a}{\sqrt{5} a} = \frac{2}{\sqrt{5}}$ .

$\vec{A B} . \vec{A O} = |\vec{A B}| . |\vec{A O}| . \cos (\vec{A B}, \vec{A O})$ = 2a . $\frac{\sqrt{5} a}{2}$ . cos $\hat{B A O}$ = = 2a . $\frac{\sqrt{5} a}{2}$ . $\frac{2}{\sqrt{5}}$ = 2a².

Vậy $\vec{A B} . \vec{A O} = 2 a^{2}$ .

b) Do AB $⊥$ AD nên $\vec{A B} ⊥ \vec{A D}$ do đó $\vec{A B} . \vec{A D} = 0$ .

Bài 3 trang 101 Toán lớp 10 Tập 1: Cho ba điểm O, A, B thẳng hàng và OA = a, OB = b. Tính tích vô hướng $\vec{O A} . \vec{O B}$ trong hai trường hợp:

a) Điểm O nằm ngoài đoạn thẳng AB;

b) Điểm O nằm trong đoạn thẳng AB.

Lời giải:

Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ - Chân trời sáng tạo (ảnh 1)

Do O nằm ngoài đoạn thẳng AB nên hai vectơ $\vec{O A}$ và $\vec{O B}$ cùng hướng.

Do đó $(\vec{O A}, \vec{O B})$ = 0^o.

Khi đó $\vec{O A} . \vec{O B} = |\vec{O A}| . |\vec{O B}| . \cos (\vec{O A}, \vec{O B})$ = a . b . cos 0^o = a.b.

Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ - Chân trời sáng tạo (ảnh 1)

Do O nằm trong đoạn thẳng AB nên hai vectơ $\vec{O A}$ và $\vec{O B}$ ngược hướng.

Do đó $(\vec{O A}, \vec{O B})$ = 180^o.

Khi đó $\vec{O A} . \vec{O B} = |\vec{O A}| . |\vec{O B}| . \cos (\vec{O A}, \vec{O B})$ = a . b . cos 180^o = -a.b.

Bài 4 trang 101 Toán lớp 10 Tập 1: Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng: $\vec{M A} . \vec{M B} = M O^{2} - O A^{2}$ .

Lời giải:

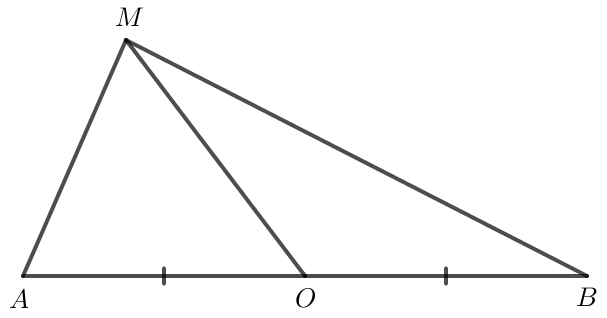
Giải Toán 10 Bài 4: Tích vô hướng của hai vectơ - Chân trời sáng tạo (ảnh 1)

Do O là trung điểm của AB nên $- \vec{O A} = \vec{O B}$ .

Khi đó $\vec{M A} . \vec{M B} = (\vec{M O} + \vec{O A}) . (\vec{M O} + \vec{O B}) = (\vec{M O} + \vec{O A}) . (\vec{M O} - \vec{O A})$

$= {\vec{M O}}^{2} - {\vec{O A}}^{2}$ = MO² - OA².

Vậy $\vec{M A} . \vec{M B}$ = MO² - OA².

Bài 5 trang 101 Toán lớp 10 Tập 1: Một người dùng một lực $\vec{F}$ có độ lớn là 90 N làm một vật dịch chuyển một đoạn 100 m. Biết lực $\vec{F}$ hợp với hướng dịch chuyển một góc 60°. Tính công sinh bởi lực $\vec{F}$ .

Lời giải:

Công sinh bởi lực $\vec{F}$ bằng: $\vec{F} . \vec{d} = |\vec{F}| . |\vec{d}| . c o s (\vec{F}, \vec{d}) =$ 90 . 100 . cos 60^o = 4 500 J.

Vậy công sinh bởi lực $\vec{F}$ bằng 4 500 J.

Bài 6 trang 101 Toán lớp 10 Tập 1: Cho hai vectơ có độ dài lần lượt là 3 và 4 và có tích vô hướng là – 6. Tính góc giữa hai vectơ đó.

Lời giải:

Gọi hai vectơ đó lần lượt là $\vec{a}$ và $\vec{b}$ .

Khi đó ta có $\vec{a} . \vec{b} = |\vec{a}| . |\vec{b}| . \cos (\vec{a}, \vec{b})$ = -6.

$\Rightarrow$ 3 . 4 . $\cos (\vec{a}, \vec{b})$ = -6

$\Rightarrow \cos (\vec{a}, \vec{b}) = \frac{- 1}{2}$

$\Rightarrow (\vec{a}, \vec{b})$ = 120^o.

Vậy góc giữa hai vectơ đó bằng 120^o.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ

Câu hỏi liên quan

Cho hình vuông ABCD có cạnh bằng a. Tính các tích vô hướng: vectơ AB.vectơ AD, vectơ AB.vectơ AC, vectơ AC.vectơ CB, vectơ AC.vectơ BD

AC là độ dài cạnh huyền của tam giác vuông cân có cạnh bằng a nên
Xem thêm

Cho tam giác đều ABC có H là trung điểm của cạnh BC. Tìm các góc: (vectơ AB, vectơ AC),(vectơ AB, vectơ BC),(vectơ AH,vectơ BC)

Dựng hình bình hành ABCD.
Xem thêm

Cho hai vectơ i, j vuông góc, cùng có độ dài bằng 1. a) Tính: (vectơ i + vectơ j)^2; (vectơ i - vectơ j)^2; (vectơ i + vectơ j).(vectơ i - vectơ j)

Do hai vectơ i, j vuông góc
Xem thêm

Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng: vectơ MA.vectơ MB = MO^2 - OA^2

Do O là trung điểm của AB
Xem thêm

Cho hình vuông ABCD có tâm I (Hình 1). a) Tính góc IDC

a) Hình vuông ABCD có tâm I nên IA = IB = IC = ID
Xem thêm

Cho hai vectơ có độ dài lần lượt là 3 và 4 và có tích vô hướng là – 6. Tính góc giữa hai vectơ đó

Vậy góc giữa hai vectơ đó bằng 120độ
Xem thêm

Cho tam giác ABC vuông cân tại A, cạnh huyền bằng căn 2. Tính các tích vô hướng: vectơ AB.vectơ AC, vectơ AC.vectơ BC, vectơ BA.vectơ BC

Do tam giác ABC vuông cân tại A nên AB vuông góc AC.
Xem thêm

Phân tử sulfur dioxide (SO2) có cấu tạo hình chữ V, góc liên kết OSO gần bằng 120°. Người ta biểu diễn sự phân cực giữa nguyên tử S

Vậy độ dài của vectơ u bằng 1,6 đơn vị.
Xem thêm

Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính: a) vectơ AB . vectơ AO

a) AC là độ dài cạnh huyền của tam giác vuông có độ dài hai cạnh lần lượt là 2a và a.
Xem thêm

Hai vectơ a và b có độ dài lần lượt là 3 và 8 và có tích vô hướng là 12 căn 2. Tính góc giữa hai vectơ a và b

Vậy góc giữa hai vectơ a và b bằng 45°.
Xem thêm

Xem tất cả hỏi đáp với chuyên mục: Tích vô hướng của hai vectơ CTST

Được cập nhật 11/09/2023 538 lượt xem

Bởi vietjack3

Chủ đề: giải sgk toán 10 Tích vô hướng của hai vectơ

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Giải sgk Toán 10 - CTST

Giải SGK Toán 10 (Chân trời sáng tạo) Bài 4: Ba đường conic trong mặt phẳng tọa độ

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 10 Bài 4: Ba đường conic trong mặt phẳng tọa độ sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 4. Mời các bạn đón xem:

706 1 năm trước

Giải sgk Toán 10 - CTST

Giải SGK Toán 10 (Chân trời sáng tạo) Bài tập cuối chương 9 trang 73, 74, 75

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 10 Bài tập cuối chương 9 trang 73, 74, 75 sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10. Mời các bạn đón xem:

360 1 năm trước

Giải sgk Toán 10 - CTST

Giải SGK Toán 10 (Chân trời sáng tạo) Bài 1: Không gian mẫu và biến cố

1900.edu.vn xin giới thiệu giải bài tập Toán lớp 10 Bài 1: Không gian mẫu và biến cố sách Chân trời sáng tạo hay nhất, chi tiết giúp học sinh dễ dàng làm bài tập Toán 10 Bài 1. Mời các bạn đón xem:

409 1 năm trước