Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính: a) vectơ AB . vectơ AO

Bài 2 trang 101 Toán lớp 10 Tập 1: Cho hình chữ nhật ABCD có tâm O và cho AD = a, AB = 2a. Tính:

a) $\overrightarrow{AB}.\overrightarrow{AO}$

b) $\overrightarrow{AB}.\overrightarrow{A\text{D}}$

Trả lời

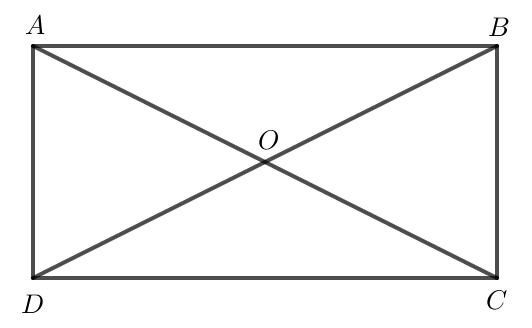
a) AC là độ dài cạnh huyền của tam giác vuông có độ dài hai cạnh lần lượt là 2a và a.

Do đó AC = $\sqrt{{\left(2\text{a}\right)}^2+a^2}=\sqrt{5}a$ (do AC là độ dài đoạn thẳng nên AC > 0).

Hình chữ nhật ABCD có tâm O nên O là trung điểm của AC.

Do đó AO = $\frac{1}{2}$AC = $\frac{\sqrt{5}a}{2}$.

Tam giác ABC vuông tại B nên $\text{cos}\widehat{BAC}=\frac{AB}{AC}=\frac{2a}{\sqrt{5}a}=\frac{2}{\sqrt{5}}$.

$\overrightarrow{AB}.\overrightarrow{AO}=\left|\overrightarrow{AB}\right|.\left|\overrightarrow{AO}\right|.\cos \left(\overrightarrow{AB},\overrightarrow{AO}\right)$ = 2a . $\frac{\sqrt{5}a}{2}$ . cos $\widehat{BAO}$ = = 2a . $\frac{\sqrt{5}a}{2}$ . $\frac{2}{\sqrt{5}}$ = 2a².

Vậy $\overrightarrow{AB}.\overrightarrow{AO}=2a^2$.

b) Do AB $\perp$ AD nên $\overrightarrow{AB}\perp \overrightarrow{A\text{D}}$ do đó $\overrightarrow{AB}.\overrightarrow{A\text{D}}=0$.

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ