Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng: vectơ MA.vectơ MB = MO^2 - OA^2

Bài 4 trang 101 Toán lớp 10 Tập 1: Cho đoạn thẳng AB có O là trung điểm và cho điểm M tùy ý. Chứng minh rằng: $\overrightarrow{MA}.\overrightarrow{MB}=M{O}^2-O{A}^2$.

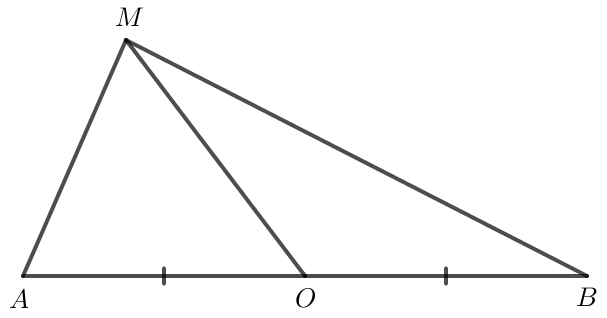
Do O là trung điểm của AB nên $-\overrightarrow{OA}=\overrightarrow{OB}$.

Khi đó $\overrightarrow{MA}.\overrightarrow{MB}=\left(\overrightarrow{MO}+\overrightarrow{OA}\right).\left(\overrightarrow{MO}+\overrightarrow{OB}\right)=\left(\overrightarrow{MO}+\overrightarrow{OA}\right).\left(\overrightarrow{MO}-\overrightarrow{OA}\right)$

$={\overrightarrow{MO}}^2-{\overrightarrow{OA}}^2$ = MO² - OA².

Vậy $\overrightarrow{MA}.\overrightarrow{MB}$ = MO² - OA².

Trả lời

Do O là trung điểm của AB nên $-\overrightarrow{OA}=\overrightarrow{OB}$.

Khi đó $\overrightarrow{MA}.\overrightarrow{MB}=\left(\overrightarrow{MO}+\overrightarrow{OA}\right).\left(\overrightarrow{MO}+\overrightarrow{OB}\right)=\left(\overrightarrow{MO}+\overrightarrow{OA}\right).\left(\overrightarrow{MO}-\overrightarrow{OA}\right)$

$={\overrightarrow{MO}}^2-{\overrightarrow{OA}}^2$ = MO² - OA².

Vậy $\overrightarrow{MA}.\overrightarrow{MB}$ = MO² - OA².

Xem thêm lời giải bài tập SGK Toán lớp 10 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Tổng và hiệu của hai vectơ

Bài 3: Tích của một số với một vectơ

Bài 4: Tích vô hướng của hai vectơ

Bài tập cuối chương 5

Bài 1: Số gần đúng và sai số

Bài 2: Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ