Giải SBT Toán 8 (Kết nối tri thức) Bài 23: Phép cộng và phép trừ phân thức đại số

Sách bài tập Toán 8 Bài 23: Phép cộng và phép trừ phân thức đại số

Bài tập 6.15 trang 9 SBT Toán 8 Tập 2: Tính các tổng sau:

a) $\frac{x^2-2}{x{\left(x-1\right)}^2}+\frac{2-x}{x{\left(x-1\right)}^2}$;

b) $\frac{1-2x}{6x^{3}y}+\frac{3+2x}{6x^{3}y}+\frac{2x-4}{6x^{3}y}$.

Lời giải:

a) $\frac{x^2-2}{x{\left(x-1\right)}^2}+\frac{2-x}{x{\left(x-1\right)}^2}$

$=\frac{x^2-2+2-x}{x{\left(x-1\right)}^2}$$=\frac{x^2-x}{x{\left(x-1\right)}^2}$

$=\frac{x\left(x-1\right)}{x{\left(x-1\right)}^2}=\frac{1}{x-1}$

b) $\frac{1-2x}{6x^{3}y}+\frac{3+2x}{6x^{3}y}+\frac{2x-4}{6x^{3}y}$

=$\frac{1-2x+3+2x+2x-4}{6x^{3}y}$

=$\frac{2x}{6x^{3}y}=\frac{1}{3x^{2}y}$

Bài tập 6.16 trang 9 SBT Toán 8 Tập 2: Tính các hiệu sau:

a) $\frac{2x^2-1}{x^2-3x}-\frac{\left(x-1\right)\left(x+1\right)}{x^2-3x}$;

b) $\frac{1}{2x-3}-\frac{13}{\left(2x-3\right)\left(4x+7\right)}$.

Lời giải:

a) $\frac{2x^2-1}{x^2-3x}-\frac{\left(x-1\right)\left(x+1\right)}{x^2-3x}$

= $\frac{2x^2-1}{x^2-3x}-\frac{x^2-1}{x^2-3x}$

= $\frac{2x^2-1-\left(x^2-1\right)}{x^2-3x}$

= $\frac{2x^2-1-x^2+1}{x^2-3x}$

= $\frac{x^2}{x^2-3x}$

= $\frac{x^2}{x\left(x-3\right)}=\frac{x}{x-3}$

b) $\frac{1}{2x-3}-\frac{13}{\left(2x-3\right)\left(4x+7\right)}$

= $\frac{4x+7}{\left(2x-3\right)\left(4x+7\right)}-\frac{13}{\left(2x-3\right)\left(4x+7\right)}$ (Mẫu thức chung là: (2x – 3)(4x + 7))

= $\frac{4x+7-13}{\left(2x-3\right)\left(4x+7\right)}$

= $\frac{4x-6}{\left(2x-3\right)\left(4x+7\right)}$

= $\frac{2\left(2x-3\right)}{\left(2x-3\right)\left(4x+7\right)}$

= $\frac{2}{4x+7}$.

Bài tập 6.17 trang 9 SBT Toán Tập 2: Tính:

a) $\frac{5x+y^2}{x^{2}y}-\frac{5y-x^2}{x{y}^2}$;

b) $\frac{y}{2x^2-xy}+\frac{4x}{y^2-2xy}$.

Lời giải:

a) $\frac{5x+y^2}{x^{2}y}-\frac{5y-x^2}{x{y}^2}$

$=\frac{y\left(5x+y^2\right)}{x^2{y}^2}-\frac{x\left(5y-x^2\right)}{x^2{y}^2}$(Mẫu thức chung là: x²y²)

$=\frac{5xy+y^3}{x^2{y}^2}-\frac{5xy-x^3}{x^2{y}^2}$

$=\frac{5xy+y^3-5xy+x^3}{x^2{y}^2}=\frac{x^3+y^3}{x^2{y}^2}$

b) $\frac{y}{2x^2-xy}+\frac{4x}{y^2-2xy}$=$\frac{y}{x\left(2x-y\right)}+\frac{4x}{y\left(y-2x\right)}$

=$\frac{-y^2}{xy\left(y-2x\right)}+\frac{4x^2}{xy\left(y-2x\right)}$ (Mẫu thức chung là: xy(y – 2x))

= $\frac{-y^2+4x^2}{xy\left(y-2x\right)}$= $\frac{{\left(2x\right)}^2-y^2}{xy\left(y-2x\right)}$ = $\frac{\left(2x-y\right)\left(2x+y\right)}{xy\left(y-2x\right)}$

=$\frac{-\left(y-2x\right)\left(2x+y\right)}{xy\left(y-2x\right)}$ = $\frac{-2x-y}{xy}$.

Bài tập 6.18 trang 9 SBT Toán Tập 2: Tính các tổng sau:

a) $\frac{5}{6x^{2}y}+\frac{7}{12x{y}^2}+\frac{11}{18xy}$;

b) $\frac{x^3+2x}{x^3+1}+\frac{2x}{x^2-x+1}+\frac{1}{x+1}$.

Lời giải:

a) $\frac{5}{6x^{2}y}+\frac{7}{12x{y}^2}+\frac{11}{18xy}$

= $\frac{30y}{36x^2{y}^2}+\frac{21x}{36x^2{y}^2}+\frac{22xy}{36x^2{y}^2}$ (Mẫu thức chung là: 36x²y²)

= $\frac{30y+21x+22xy}{36x^2{y}^2}$.

b) $\frac{x^3+2x}{x^3+1}+\frac{2x}{x^2-x+1}+\frac{1}{x+1}$

= $\frac{x^3+2x}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{2x}{x^2-x+1}+\frac{1}{x+1}$

= $\frac{x^3+2x}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{2x\left(x+1\right)}{\left(x+1\right)\left(x^2-x+1\right)}+\frac{x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}$

= $\frac{x^3+2x+2x\left(x+1\right)+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}$

= $\frac{x^3+2x+2x^2+2x+x^2-x+1}{\left(x+1\right)\left(x^2-x+1\right)}$

=$\frac{x^3+3x^2+3x+1}{\left(x+1\right)\left(x^2-x+1\right)}$

= $\frac{{\left(x+1\right)}^3}{\left(x+1\right)\left(x^2-x+1\right)}$

= $\frac{{\left(x+1\right)}^2}{x^2-x+1}$.

Bài tập 6.19 trang 9 SBT Toán 8 Tập 2: a) Rút gọn biểu thức $P=\frac{x^4}{1-x}+x^3+x^2+x+1$.

b) Tính giá trị của P tại x = –99.

Lời giải:

a)

Điều kiện xác định của biểu thức là x ≠ 1, ta có:

$P=\frac{x^4}{1-x}+x^3+x^2+x+1$

$=\frac{x^4}{1-x}+\frac{x^3\left(1-x\right)}{1-x}+\frac{x^2\left(1-x\right)}{1-x}+\frac{x\left(1-x\right)}{1-x}+\frac{1-x}{1-x}$

$=\frac{x^4+x^3\left(1-x\right)+x^2\left(1-x\right)+x\left(1-x\right)+\left(1-x\right)}{1-x}$

$=\frac{x^4+x^3-x^4+x^2-x^3+x-x^2+1-x}{1-x}$

$=\frac{1}{1-x}$

b) Thay x = –99 vào biểu thức P ta có:

$P=\frac{1}{1-(-99)}=\frac{1}{100}$.

Bài tập 6.20 trang 10 SBT Toán 8 Tập 2: a) Rút gọn biểu thức: $Q=\frac{18}{\left(x-3\right)\left(x^2-9\right)}-\frac{3}{x^2-6x+9}-\frac{x}{x^2-9}$.

b) Tính giá trị của Q tại x = 103.

Lời giải:

a) Điều kiện xác định của Q là: x ≠ ± 3.

Ta có $Q=\frac{18}{\left(x-3\right)\left(x^2-9\right)}-\frac{3}{x^2-6x+9}-\frac{x}{x^2-9}$

$=\frac{18}{\left(x-3\right)\left(x-3\right)\left(x+3\right)}-\frac{3}{{\left(x-3\right)}^2}-\frac{x}{\left(x-3\right)\left(x+3\right)}$

$=\frac{18}{{\left(x-3\right)}^2\left(x+3\right)}-\frac{3\left(x+3\right)}{{\left(x-3\right)}^2\left(x+3\right)}-\frac{x\left(x-3\right)}{{\left(x-3\right)}^2\left(x+3\right)}$

$=\frac{18-3\left(x+3\right)-x\left(x-3\right)}{{\left(x-3\right)}^2\left(x+3\right)}$

$=\frac{18-3x-9-x^2+3x}{{\left(x-3\right)}^2\left(x+3\right)}$

$=\frac{-x^2+9}{{\left(x-3\right)}^2\left(x+3\right)}$

$=\frac{\left(3-x\right)\left(3+x\right)}{{\left(3-x\right)}^2\left(x+3\right)}=\frac{1}{3-x}$.

b) Thay x = 103 vào Q ta có: Q = $\frac{1}{3-103}=\frac{-1}{100}$.

Bài tập 6.21 trang 10 SBT Toán 8 Tập 2: a) Chứng minh rằng nếu a, b, c ≠ 0, a + b + c = 0 thì $\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=0$.

b) Chứng minh rằng nếu x ≠ y, y ≠ z, z ≠ x thì:

$\frac{1}{\left(x-y\right)\left(y-z\right)}+\frac{1}{\left(y-z\right)\left(z-x\right)}+\frac{1}{\left(z-x\right)\left(x-y\right)}=0$.

Lời giải:

a) Với a, b, c ≠ 0, ta có:

$\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}$

$=\frac{c}{abc}+\frac{a}{abc}+\frac{b}{abc}$

$=\frac{a+b+c}{abc}$

Mà a + b + c = 0 nên ta suy ra: $\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}=\frac{0}{abc}=0$ (điều cần phải chứng minh).

b) Với x ≠ y, y ≠ z, z ≠ x, ta có:

$\frac{1}{\left(x-y\right)\left(y-z\right)}+\frac{1}{\left(y-z\right)\left(z-x\right)}+\frac{1}{\left(z-x\right)\left(x-y\right)}$

$=\frac{z-x}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}+\frac{x-y}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}+\frac{y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}$

$=\frac{z-x+x-y+y-z}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=\frac{0}{\left(x-y\right)\left(y-z\right)\left(z-x\right)}=0$.

Vậy $\frac{1}{\left(x-y\right)\left(y-z\right)}+\frac{1}{\left(y-z\right)\left(z-x\right)}+\frac{1}{\left(z-x\right)\left(x-y\right)}=0$ (điều cần phải chứng minh).

Bài tập 6.22 trang 10 SBT Toán 8 Tập 2: Cho biểu thức $P=\frac{x}{y-2}+\frac{2x-3y}{x-6}$. Chứng minh rằng x, y thay đổi luôn thỏa mãn điều kiện 3y – x = 6 thì P có giá trị không đổi.

Lời giải:

Điều kiện xác định của P là: y ≠ 2, x ≠ 6.

Nếu 3y – x = 6 thì x = 3y – 6. Thay x = 3y – 6 vào biểu thức P ta có:

$P=\frac{x}{y-2}+\frac{2x-3y}{x-6}$

$=\frac{3y-6}{y-2}+\frac{2.\left(3y-6\right)-3y}{\left(3y-6\right)-6}$

$=\frac{3y-6}{y-2}+\frac{6y-12-3y}{3y-6-6}$

$=\frac{3\left(y-2\right)}{y-2}+\frac{3y-12}{3y-12}=3+1=4$ không đổi với mọi x, y thỏa mãn 3y – x = 6.

Bài tập 6.23 trang 10 SBT Toán Tập 2: Cho biểu thức

$P=\frac{2x-6}{x^3-3x^2-x+3}+\frac{2x^2}{1-x^2}-\frac{6}{x-3}$ (x ≠ 3, x ≠ 1, x ≠ –1).

a) Rút gọn phân thức $\frac{2x-6}{x^3-3x^2-x+3}$.

b) Chứng tỏ rằng có thể viết $P=a+\frac{b}{x-3}$ trong đó a, b là những hằng số.

c) Tìm tập hợp các giá trị nguyên của x để P có giá trị là số nguyên.

Lời giải:

a) Ta có $\frac{2x-6}{x^3-3x^2-x+3}$$=\frac{2\left(x-3\right)}{\left(x^3-3x^2\right)-\left(x-3\right)}$

$=\frac{2\left(x-3\right)}{x^2\left(x-3\right)-\left(x-3\right)}$$=\frac{2\left(x-3\right)}{\left(x-3\right)\left(x^2-1\right)}$$=\frac{2}{x^2-1}$

b) $P=\frac{2x-6}{x^3-3x^2-x+3}+\frac{2x^2}{1-x^2}-\frac{6}{x-3}$

$=\frac{2}{x^2-1}+\frac{2x^2}{1-x^2}-\frac{6}{x-3}$

$=\frac{-2}{1-x^2}+\frac{2x^2}{1-x^2}-\frac{6}{x-3}$

$=\left(\frac{-2}{1-x^2}+\frac{2x^2}{1-x^2}\right)-\frac{6}{x-3}$

$=\frac{-2\left(1-x^2\right)}{1-x^2}-\frac{6}{x-3}$

$=-2-\frac{6}{x-3}=-2+\frac{-6}{x-3}$

Do đó, P có thể viết dưới dạng $P=a+\frac{b}{x-3}$ trong đó a = –2; b = –6.

c) Vì $P=-2-\frac{6}{x-3}$nên để P là số nguyên thì $\frac{6}{x-3}$ phải là số nguyên.

Suy ra 6 ⋮ (x – 3) hay (x – 3) ∈ Ư(6).

Khi đó (x – 3) ∈ {1; 2; 3; 6; –1; –2; –3; –6}.

Suy ra x ∈ {4; 5; 6; 9; 2; 1; 0; –3}.

Loại x = 1 vì không thỏa mãn điều kiện x ≠ 3, x ≠ 1, x ≠ –1.

Vậy x ∈ {4; 5; 6; 9; 2; 0; –3} thì thỏa mãn yêu cầu đề bài.

Bài tập 6.24 trang 10 SBT Toán 8 Tập 2: a) Rút gọn biểu thức $P=\frac{x^2+2x}{x^3-1}-\frac{1}{x^2-x}-\frac{1}{x^2+x+1}$ (x ≠ 0, x ≠ 1).

b) Chứng tỏ rằng chỉ có một giá trị nguyên của của x để P cũng nhận giá trị nguyên

Lời giải:

a) Ta có:

$P=\frac{x^2+2x}{x^3-1}-\frac{1}{x^2-x}-\frac{1}{x^2+x+1}$ (x ≠ 0, x ≠ 1)

$=\frac{x^2+2x}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{1}{x\left(x-1\right)}-\frac{1}{x^2+x+1}$

$=\frac{\left(x^2+2x\right)x}{x\left(x-1\right)\left(x^2+x+1\right)}-\frac{x^2+x+1}{x\left(x-1\right)\left(x^2+x+1\right)}-\frac{x\left(x-1\right)}{x\left(x-1\right)\left(x^2+x+1\right)}$

$=\frac{\left(x^2+2x\right)x-\left(x^2+x+1\right)-x\left(x-1\right)}{x\left(x-1\right)\left(x^2+x+1\right)}$

$=\frac{x^3+2x^2-x^2-x-1-x^2+x}{x\left(x-1\right)\left(x^2+x+1\right)}$$=\frac{x^3-1}{x\left(x-1\right)\left(x^2+x+1\right)}$

$=\frac{\left(x-1\right)\left(x^2+x+1\right)}{x\left(x-1\right)\left(x^2+x+1\right)}$$=\frac{1}{x}$

b) Để P nguyên thì 1 ⋮ x, tức là x ∈ Ư(1).

Suy ra x ∈ Ư(1) = {1; –1}.

Mà điều kiện xác định của P là x ≠ 0, x ≠ 1 nên ta loại trường hợp x = 1.

Do đó, chỉ có một giá trị x = –1 thỏa mãn yêu cầu đề bài.

Bài tập 6.25 trang 10 SBT Toán 8 Tập 2: Một tàu chở hàng đi từ cảng A đến cảng B cách nhau 900 km với vận tốc không đổi là x (km/h). Khi đi được $\frac{1}{3}$ quãng đường thì một động cơ của tàu bị hỏng nên tàu chỉ còn chạy với vận tốc 12 km/h trong suốt 3 giờ tàu sửa chữa động cơ. Để về cảng B không muộn hơn dự định, tàu phải tăng vận tốc thêm 5 km/h. Viết phân thức tính thời gian thực tế để tàu đi từ cảng A đến cảng B.

Lời giải:

Quãng đường tàu đi với vận tốc x (km/h) là: $900.\frac{1}{3}$= 300 (km).

Thời gian tàu đi với vận tốc x (km/h) là: $\frac{300}{x}$ (giờ).

Quãng đường tàu đi với vận tốc 12 km/h là: 12 . 3 = 36 (km).

Quãng đường còn lại dài: 900 – 300 – 36 = 564 (km).

Vận tốc tàu đi trên quãng đường 564 km là: x + 5 (km/h).

Thời gian tàu đi quãng đường 564 km là: $\frac{564}{x+5}$ (giờ).

Thời gian thực tế tàu đi là:

$\frac{300}{x}+3+\frac{564}{x+5}=\frac{300\left(x+5\right)}{x\left(x+5\right)}+\frac{3x\left(x+5\right)}{x\left(x+5\right)}+\frac{564x}{x\left(x+5\right)}$

$=\frac{300x+1500+3x^2+15x+564x}{x\left(x+5\right)}$

$=\frac{3x^2+879x+1500}{x\left(x+5\right)}$(giờ)

Vậy phân thức tính thời gian thực tế để tàu đi từ cảng A đến cảng B là:

$\frac{3x^2+879x+1500}{x\left(x+5\right)}$ giờ.

Bài tập 6.26 trang 10 SBT Toán 8 Tập 2: Cho hai hình hộp chữ nhật bằng nhau cùng có thể tích 200 cm³ và một hình hộp chữ nhật có thể tích 500 cm³ sắp xếp như trong hình bên (độ dài các cạnh hình hộp được tính bằng đơn vị cm). Viết các phân thức biểu thị độ dài (tính bằng cm) của các đoạn thẳng AC và DE.

Lời giải:

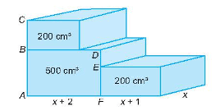
Gọi y (cm) là độ dài đoạn thẳng DE. (y > 0).

Ta có: AB = DE + EF

Vì hình hộp chữ nhật 200 cm³ có diện tích đáy là: (x + 1)x (cm²), từ đó suy ra chiều cao EF = $\frac{200}{x\left(x+1\right)}$ (cm).

Vì hình hộp chữ nhật 500 cm³ có diện tích đáy là: (x + 2)x (cm²), từ đó suy ra chiều cao AB = $\frac{500}{x\left(x+2\right)}$(cm).

Vì AB = DE + EF

Suy ra DE = AB – EF = $\frac{500}{x\left(x+2\right)}$$-\frac{200}{x\left(x+1\right)}$

= $\frac{500\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)}-\frac{200\left(x+2\right)}{x\left(x+1\right)\left(x+2\right)}$

= $\frac{500\left(x+1\right)-200\left(x+2\right)}{x\left(x+1\right)\left(x+2\right)}$

$=\frac{500x+500-200x-400}{x\left(x+1\right)\left(x+2\right)}$

$=\frac{300x+100}{x\left(x+1\right)\left(x+2\right)}$

Ta lại có:

CB = EF = $\frac{200}{x\left(x+1\right)}$ (cm) (vì hai hình hộp chữ nhật bằng nhau có cùng thể tích 200 cm²).

AC = CB + AB = $\frac{200}{x\left(x+1\right)}$ + $\frac{500}{x\left(x+2\right)}$

= $\frac{500\left(x+1\right)}{x\left(x+1\right)\left(x+2\right)}+\frac{200\left(x+2\right)}{x\left(x+1\right)\left(x+2\right)}$

= $\frac{500\left(x+1\right)+200\left(x+2\right)}{x\left(x+1\right)\left(x+2\right)}$

$=\frac{500x+500+200x+400}{x\left(x+1\right)\left(x+2\right)}$

$=\frac{700x+900}{x\left(x+1\right)\left(x+2\right)}$

Vậy phân thức biểu diễn độ dài độ dài các đoạn thẳng DE và AC là

DE =$\frac{300x+100}{x\left(x+1\right)\left(x+2\right)}$ (cm) và AC = $\frac{700x+900}{x\left(x+1\right)\left(x+2\right)}$ (cm).

Xem thêm các bài giải SBT Toán lớp 8 Kết nối tri thức hay, chi tiết khác: