Giải SBT Toán 8 Bài tập cuối chương 8
Giải SBT Toán 8 trang 83
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: C
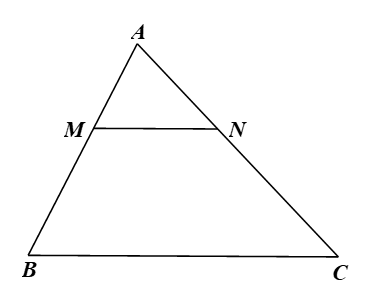
Xét ∆ABC với MN // BC, ta có (định lí Thalès)
Suy ra
Bài 57 trang 83 SBT Toán 8 Tập 2: Cho hai tam giác MNP và M’N’P’. Phát biểu nào sau đây là đúng?
A. Nếu và thì ∆MNP ᔕ ∆M’N’P’.
B. Nếu và thì ∆MNP ᔕ ∆M’N’P’.
C. Nếu và thì ∆MNP ᔕ ∆M’N’P’.
D. Nếu và thì ∆MNP ᔕ ∆M’N’P’.
Lời giải:
Đáp án đúng là: D
Xét ∆MNP và ∆M’N’P’ có:
và
Do đó ∆MNP ᔕ ∆M’N’P’ (g.g).
Vậy ta chọn phương án D.
Bài 58 trang 83 SBT Toán 8 Tập 2: Nếu ∆MNP ᔕ ∆DEG thì
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: A
Vì ∆MNP ᔕ ∆DEG nên (tỉ số đồng dạng)
Suy ra
Bài 59 trang 83 SBT Toán 8 Tập 2: Cho ∆MNP ᔕ ∆M’N’P’ và . Số đo góc P là:
A. 30°.
B. 40°.
C. 70°.
D. 110°.
Lời giải:
Đáp án đúng là: D
Do ∆MNP ᔕ ∆M’N’P’ nên (hai góc đồng dạng)
Xét ∆MNP có (tổng ba góc của một tam giác)
Suy ra =
Vậy
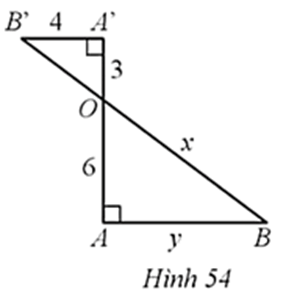
Bài 60 trang 83 SBT Toán 8 Tập 2: Hình 54 cho biết A’B’ = 4, A’O = 3, AO = 6, OB = x, AB = y
Giá trị của biểu thức x + y là:
A. 22.
B. 18.
C. 20.
D. 16.
Lời giải:
Đáp án đúng là: B
Xét ∆A’OB’ vuông tại A’ có: B’O2 = A’B’2 + A’O2 (định lí Pythagore)
Do đó =
Do A’B’ ⊥ AA’, AB ⊥ AA’ nên A’B’ // AB.
Suy ra ∆OA’B’ ᔕ ∆OAB nên (tỉ số đồng dạng)
Hay
Do đó
Vậy x + y = 10 + 8 = 18.
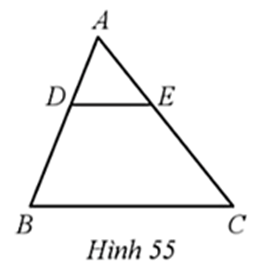
Bài 61 trang 83 SBT Toán 8 Tập 2: Cho tam giác ABC có DE // BC (Hình 55).
Khẳng định nào dưới đây đúng?
A.
B.
C.
D.
Lời giải:
Đáp án đúng là: C
Tam giác ABC có DE // BC nên theo hệ quả của định lí Thalès ta có:
Suy ra
Giải SBT Toán 8 trang 84
A. 6.
B. 9.
C. 5.
D. 8 .
Lời giải:
Đáp án đúng là: A
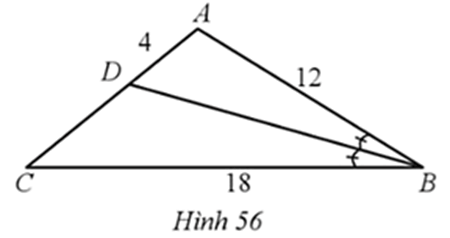
Xét ∆ABC có BD là đường phân giác góc ABC nên (tính chất đường phân giác)
Hay suy ra
Vậy DC = 6.
A. k + q.
B. kq.
C.
D.
Lời giải:
Đáp án đúng là: D
∆ABC ᔕ ∆DEF theo tỉ số đồng dạng k nên ta có (tỉ số đồng dạng).
∆MNP ᔕ ∆DEF theo tỉ số đồng dạng q nên ta có (tỉ số đồng dạng).
Ta có:
Vậy ∆ABC ᔕ ∆MNP theo tỉ số đồng dạng là
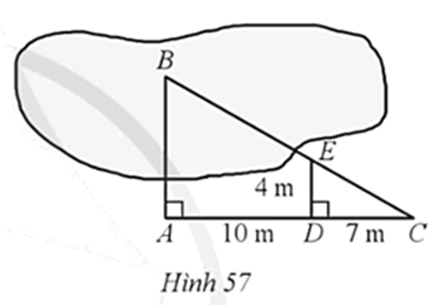
A. 9,3 m.
B. 9,4 m.
C. 9,6 m.
D. 9,7 m.
Lời giải:
Đáp án đúng là: D
Ta có AC = AD + DC = 10 + 17 = 17 (m).
Do DE ⊥ AC, BA ⊥ AC nên DE // AB
Xét ∆ABC với DE // AB, ta có (hệ quả của định lí Thalès)
Hay suy ra (m).
Vậy khoảng cách AB khoảng 9,7 m.
Lời giải:
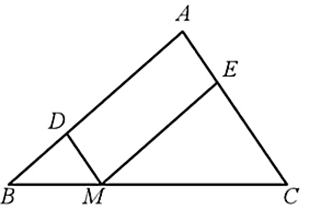
• Do MC = 2MB và MB + MC = BC nên BC = MB + 2MB = 3MB
Do đó
Vì DM // AB nên ∆BDM ᔕ ∆BAC.
Suy ra (tỉ số đồng dạng)
Do đó = = (tính chất của dãy tỉ số bằng nhau).
Mà nên
Do đó chu vi tam giác DBM là (cm).
• Do MC = 2MB hay
Do MB + MC = BC nên
Suy ra
Vì EM // AC nên ∆ECM ᔕ ∆ACB.
Suy ra (tỉ số đồng dạng)
Do đó = = (tính chất của dãy tỉ số bằng nhau).
Mà nên
Do đó chu vi tam giác ECM là (cm).
Vậy x + 2y = 10 + 2.20 = 50 (cm).
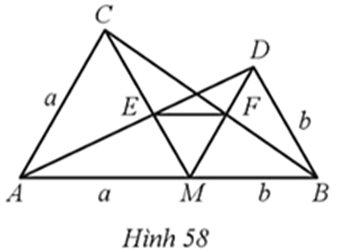
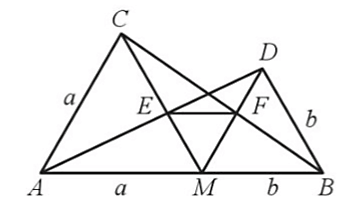
a) Chứng minh EF // AB.
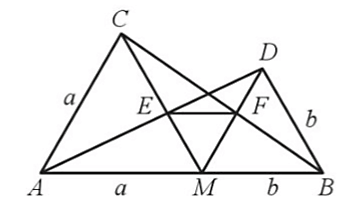
b) Tính ME, MF theo a, b.
Lời giải:
a) Do ∆AMC và ∆BMD là các tam giác đều nên ta có: AC = AM = CM = a, DM = DB = MB = b và
Mà các cặp góc này ở vị trí so le trong nên MD // AC, DB // CM.
Xét ∆ACE với MD // AC, ta có (hệ quả của định lí Thalès).
Xét ∆BDF với DB // CM, ta có (hệ quả của định lí Thalès).
Từ đó, ta có:
Xét ∆CMB có nên EF // MB hay EF // AB (do M ∈ AB).
b) Từ EF // AB (câu a) suy ra (các cặp góc ở vị trí so le trong)
Tam giác EMF có nên tam giác EMF là tam giác đều.
Do đó ME = MF = EF.
Xét ∆CMB có EF // MB nên ta có: (hệ quả của định lí Thalès).
Do đó = = = =
Hay suy ra
Vậy
Giải SBT Toán 8 trang 85
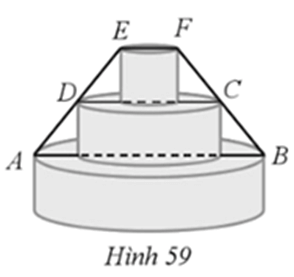
Lời giải:
Độ dài đường kính CD là: 32 ‒ 12 = 20 (cm).
Gọi H là trung điểm của EB.
Xét ∆EAB có D, H lần lượt là trung điểm của EA, EB nên DH là đường trung bình của ∆EAB. Do đó DH // AB và
Tương tự, HC là đường trung bình của ∆BEF. Do đó HC // EF và
Mà EF // AB nên DH // AB, HC // AB
Theo tiên đề Euclid ta có ba điểm D, H, C thẳng hàng.
Khi đó DC // EF // AB.
Xét ∆EAB có DH // AB nên ∆EDH ᔕ ∆EAB.
Suy ra (tỉ số đồng dạng)
Do đó (cm).
Khi đó HC = DC ‒ DH = 20 ‒ 16 = 4 (cm).
Syu ra EF = 2.HC = 2.4 = 8 (cm).
Vậy độ dài đường kính tầng trên cùng EF bằng 8 cm.
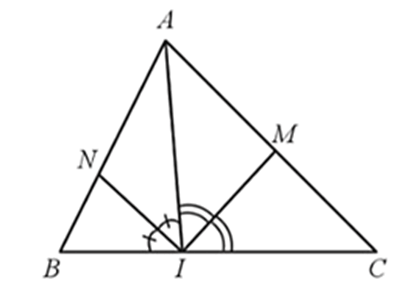
Lời giải:
Xét ∆AIC có IM là đường phân giác của các góc AIC nên (tính chất đường phân giác) (1)
Xét ∆AIB có IN là đường phân giác của các góc AIB nên (tính chất đường phân giác) (2)
Nhân lần lượt hai vế của (1), (2) với ta có:
Suy ra
Do đó: AN.BI.CM = BN.IC.AM.
Lời giải:
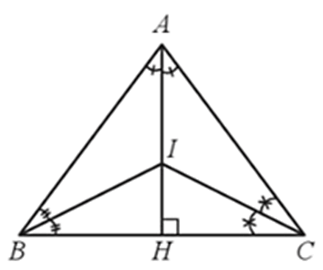
Gọi H là giao điểm của hai đường thẳng AI và BC.
Do tam giác ABC cân tại A nên đường phân giác AI cũng là đường cao, đường trung tuyến của tam giác.
Do đó (cm).
Tam giác AHB vuông tại H nên theo định lí Pythagore ta có:
AH2 = AB2 ‒ BH2 = 102 ‒ 62 = 64
Suy ra AH = 8 cm.
Xét ∆ABH có BI là phân giác góc B nên ta có: (tính chất đường phân giác)
Suy ra hay
Do đó nên (cm).
Vậy AI = 5 cm.
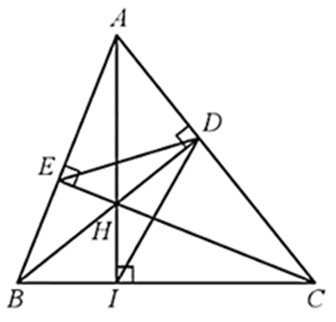
a) ∆EBH ᔕ ∆DCH, ∆ADE ᔕ ∆ABC;
b) DB là tia phân giác của góc EDI, với I là giao điểm của AH và BC.
Lời giải:
a) Do BD, CE là các đường cao nên BD ⊥ AC, CE ⊥ AB.
Xét ∆EBH và ∆DCH có:
(hai góc đối đỉnh)
Do đó ∆EBH ᔕ ∆DCH (g.g.).
Xét ∆ABD và ∆ACE có:
là góc chung
Do đó ∆ADE ᔕ ∆ABC (g.g).
Suy ra (tỉ số đồng dạng).
Xét ∆ADE và ∆ABC có:
là góc chung
Do đó ∆ADE ᔕ ∆ABC (c.g.c).
b) Do ∆ADE ᔕ ∆ABC (câu a) nên (hai góc tương ứng) (1).
Xét ∆CIA và ∆CDB có:
là góc chung
Do đó ∆CIA ᔕ ∆CDB (g.g).
Suy ra (tỉ số đồng dạng) hay
Xét ∆CDI và ∆CBA có:
là góc chung
Do đó ∆CDI ᔕ ∆CBA (c.g.c).
Suy ra (hai góc tương ứng) (2).
Từ (1) và (2), ta có
Do đó hay .
Vậy DB là đường phân giác của góc EDI.
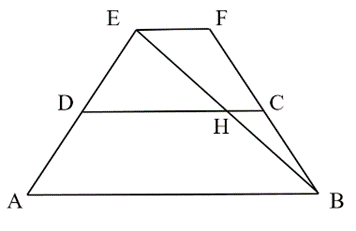
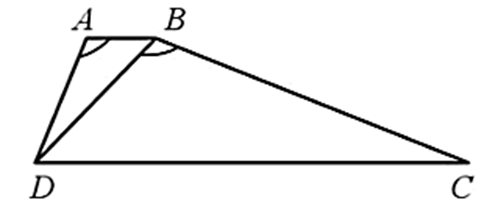
Lời giải:
Do AB // CD nên (hai góc ở vị trí so le trong)
Xét ∆ABD và ∆BDC có:
(giả thiết), (chứng minh trên)
Suy ra ∆ABD ᔕ ∆BDC (g.g).
Nên là tỉ số đồng dạng của ∆ABD ᔕ ∆BDC.
Do đó, tỉ số diện tích tam giác ABD và diện tích tam giác BDC bằng bình phương của tỉ số đồng dạng.
Suy ra diện tích tam giác ABD (kí hiệu là S∆ABD) bằng diện tích tam giác BDC (kí hiệu là S∆BDC) hay
Do đó: (cm2).
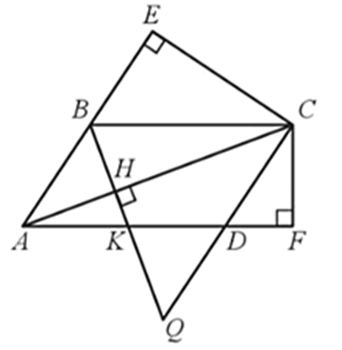
a) ∆ABH ᔕ ∆ACE; ∆CBH ᔕ ∆ACF.
b) BH2 = HK.HQ, biết tia BH cắt dường thẳng CD tại Q; cắt cạnh AD tại K.
Lời giải:
a) • Xét ∆ABH (vuông tại H) và ∆ACE (vuông tại E) có: là góc chung
Suy ra ∆ABH ᔕ ∆ACE (g.g).
• Do ABCD là hình bình hành nên AD // BC, suy ra (hai góc so le trong)
Xét ∆CBH (vuông tại H) và ACF (vuông tại F) có:
Suy ra ∆CBH ᔕ ∆ACF (g.g).
b) Do AB // CD, Q ∈ CD nên AB // CQ nên (hệ quả của định lí Thalès).
Lại có AD // BC, K ∈ AD nên BC // AK nên (hệ quả của định lí Thalès).
Suy ra hay BH2 = HK.HQ.
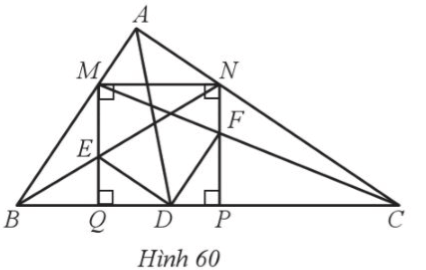
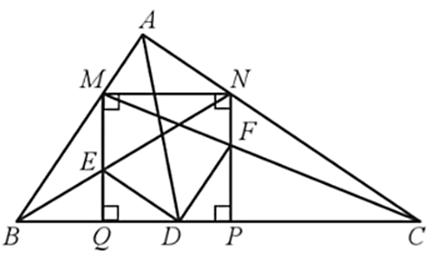
a) DE song song với AC;
b) DE = DF.
Lời giải:
a) Do MNPQ là hình vuông nên MQ // NP, mà E ∈ MQ nên EQ // NP.
Xét ∆BNP với EQ // NP, ta có (định lí Thalès) (1)
MNPQ là hình vuông nên MQ ⊥ BC, do đó tam giác BQM vuông tại Q.
Xét ∆BQM (vuông tại Q) và ∆BAC (vuông tại A) có: là góc chung
Do đó ∆BQM ᔕ ∆BAC (g.g).
Suy ra (tỉ số đồng dạng)
Hay mà QM = QP (do MNPQ là hình vuông)
Do đó (2)
Xét ∆ABC có AD là phân giác của góc BAC nên: (tính chất đường phân giác) (3)
Từ (1), (2), (3) ta có
Xét ∆NBC có nên DE // NC (định lí Thalès đảo) hay DE // AC.
b) Do DE // AC (câu a) nên (hệ quả của định lí Thalès)
Do đó
• Do MNPQ là hình vuông nên MQ // NP, mà F ∈ NP nên FP // MQ.
Xét ∆MQB với FP // MQ, ta có (định lí Thalès) (4)
Xét ∆CPN (vuông tại P) và ∆CAB (vuông tại A) có: là góc chung
Do đó ∆CPN ᔕ ∆CAB (g.g).
Suy ra (tỉ số đồng dạng) hay
Mà PQ = PN (do MNPQ là hình vuông) nên (5)
Từ ta có (6)
Từ (4), (5), (6) ta có
Xét ∆MBC có nên DF // BM (định lí Thalès đảo) hay DF // AB.
Suy ra (hệ quả của định lí Thalès), nên .
Mặt khác, ∆ABC với MN // BC (cùng vuông góc với MQ), ta có (hệ quả của định lí Thalès), do đó
Lại có nên = =
Suy ra DE = DF.
Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài 7: Trường hợp đồng dạng thứ hai của tam giác