Giải SBT Toán 8 (Cánh diều) Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Giải SBT Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Giải SBT Toán 8 trang 72

Bài 31 trang 72 SBT Toán 8 Tập 2: Tam giác thứ nhất có độ dài các cạnh là: 2,6 cm; 7,1 cm; 8 cm. Tam giác thứ hai có độ dài các cạnh là: 7,8 cm; 21,3 cm; 24 cm. Hỏi hai tam giác đó có đồng dạng không? Vì sao?

Lời giải:

Ta có: $\frac{2,6}{7,8}=\frac{26}{78}=\frac{1}{3};$ $\frac{7,1}{21,3}=\frac{71}{213}=\frac{1}{3};$ $\frac{8}{24}=\frac{1}{3}.$

Do đó: $\frac{2,6}{7,8}=\frac{7,1}{21,3}=\frac{8}{24}$

Bài 32 trang 72 SBT Toán 8 Tập 2: Tam giác ABC có độ dài các cạnh là AB = 9 cm, AC = 7 cm, BC = 15 cm. Tam giác MNP đồng dạng với tam giác ABC. Tính độ dài các cạnh của tam giác MNP, biết chu vi của nó là 46,5 cm.

Lời giải:

Do ∆MNP ᔕ ∆ABC nên $\frac{MN}{AB}=\frac{MP}{AC}=\frac{NP}{BC}$ (tỉ số đồng dạng)

Lại có chu vi của ∆ MNP là 46,5 cm nên MN + MP + NP = 46,5 (cm).

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{MN}{9}=\frac{MP}{7}=\frac{NP}{15}=\frac{MN+MP+NP}{9+7+15}=\frac{46,5}{31}=1,5$

Suy ra: MN = 9.1,5 = 13,5 (cm); MP = 7.1,5 = 10,5 (cm); NP = 15.1,5 = 22,5 (cm).

Vậy MN = 13,5 cm; MP = 10,5 cm; NP = 22,5 cm.

Bài 33 trang 72 SBT Toán 8 Tập 2: Biết tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số đồng dạng là k. Hỏi tỉ số chu vi của tam giác ABC và tam giác A’B’C’ bằng bao nhiêu?

Lời giải:

Do tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số đồng dạng là k nên $\frac{AB}{A^{\text{'}}{B}^{\text{'}}}=\frac{BC}{B^{\text{'}}{C}^{\text{'}}}=\frac{CA}{C^{\text{'}}{A}^{\text{'}}}=k.$

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

$\frac{AB}{A^{\text{'}}{B}^{\text{'}}}=\frac{BC}{B^{\text{'}}{C}^{\text{'}}}=\frac{CA}{C^{\text{'}}{A}^{\text{'}}}=\frac{AB+BC+CA}{A^{\text{'}}{B}^{\text{'}}+B^{\text{'}}{C}^{\text{'}}+C^{\text{'}}{A}^{\text{'}}}=k$

Mà chu vi tam giác ABC là AB + BC + CA;

chu vi tam giác A’B’C’ là A’B’ + B’C’ + C’A’.

Vậy tỉ số chu vi của tam giác ABC và tam giác A’B’C’ bằng k.

Bài 34 trang 72 SBT Toán 8 Tập 2: Cho tứ giác ABCD có AB = 27 cm, BC = 9 cm, BD = 8 cm, AD = 24 cm và DB² = AD.CD. Hỏi DB có thể là tia phân giác của góc ADC hay không? Vì sao?

Lời giải:

Ta có: $\frac{AB}{CB}=\frac{27}{9}=3; \frac{AD}{BD}=\frac{24}{8}=3$. Do đó $\frac{AB}{CB}=\frac{AD}{BD}$

Mặt khác, DB² = AD.CD nên $\frac{AD}{BD}=\frac{BD}{CD}$

Suy ra $\frac{AB}{CB}=\frac{AD}{BD}=\frac{BD}{CD}$

Do đó ∆BAD ᔕ ∆CBD.

Nên $\widehat{ADB}=\widehat{BDC}$ (hai góc tương ứng)

Vậy DB là tia phân giác của góc ADC.

Bài 35 trang 72 SBT Toán 8 Tập 2: Cho tam giác IKH và tam giác I’K’H’ có $\widehat{IKH}=90°$, $\widehat{KHI}=60°$, $\widehat{I^{\text{'}}{K}^{\text{'}}{H}^{\text{'}}}=90°$, $\widehat{K^{\text{'}}{I}^{\text{'}}{H}^{\text{'}}}=30°$. Chứng minh: ∆I’K’H’ ᔕ ∆IKH.

Lời giải:

Gọi H’’ là điểm đối xứng với H qua K. Khi đó KH = KH’’.

Xét ∆IKH và ∆IKH’’ có:

$\widehat{IKH}=\widehat{IK{H}^{\text{'}\text{'}}}=90°$; IK là cạnh chung; KH = KH’’.

Do đó ∆IKH = ∆IKH’’ (hai cạnh góc vuông)

Suy ra IH = IH’’ (hai cạnh tương ứng)

Nên tam giác IHH’’ cân tại I.

Lại có $\widehat{IH{H}^{\text{'}\text{'}}}=\widehat{IHK}=60°$ nên tam giác IHH’’ đều.

Suy ra IH = HH’’

Mà HH’’ = 2HK nên IH = 2HK.

Đặt HK = a (a > 0). Khi đó IH = 2a.

Xét ∆IKH có $\widehat{IKH}=90°$ nên ∆IKH vuông tại K, theo định lí Pythagore ta có:

IH² = IK² + KH²

Suy ra IK² = IH² – KH² = (2a)² – a² = 3a²

Do đó $IK=a\sqrt{3}.$

Tương tự, tam giác I’K’H’ có độ dài các cạnh là H’K’ = b (b > 0), I’H’ = 2b và $I^{\text{'}}{K}^{\text{'}}=b\sqrt{3}.$

Suy ra $\frac{I^{\text{'}}{K}^{\text{'}}}{IK}=\frac{I^{\text{'}}{H}^{\text{'}}}{IH}=\frac{H^{\text{'}}{K}^{\text{'}}}{HK}=\frac{b}{a}.$

Do đó ∆I’K’H’ ᔕ ∆IKH (c.c.c).

Bài 36 trang 72 SBT Toán 8 Tập 2: Quan sát Hình 32 có $\widehat{BAC}=90°$, $\widehat{BCD}=90°$, DB = 10,8 cm, BC = 7,2 cm và CA = 4,8 cm. Chứng minh ∆DBC ᔕ ∆BCA.

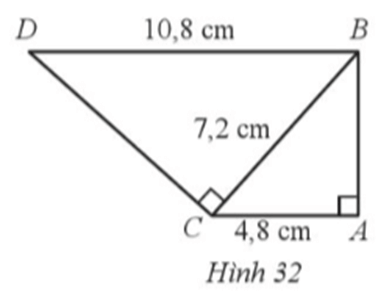
Lời giải:

Nhận thấy: $\frac{DB}{CB}=\frac{10,8}{7,2}=\frac{3}{2}, \frac{BC}{CA}=\frac{7,2}{4,8}=\frac{3}{2}$

Do đó $\frac{DB}{CB}=\frac{BC}{CA}=\frac{3}{2}.$

Xét ∆DBC và ∆BCA có:

$\widehat{BCD}=\widehat{CAB}=90°$ và $\frac{DB}{CB}=\frac{BC}{CA}$

Suy ra ∆DBC ᔕ ∆BCA (cạnh huyền và cạnh góc vuông tương ứng tỉ lệ).

Vậy ∆DBC ᔕ ∆BCA.

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác: