Cho điểm M thuộc đoạn thẳng AB, với MA = a, MB = b. Vẽ hai tam giác đều AMC và BMD; gọi E là giao điểm của AD và CM

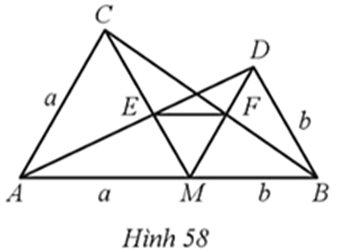
Bài 66 trang 84 SBT Toán 8 Tập 2: Cho điểm M thuộc đoạn thẳng AB, với MA = a, MB = b. Vẽ hai tam giác đều AMC và BMD; gọi E là giao điểm của AD và CM, F là giao điểm của DM và BC (Hình 58).

a) Chứng minh EF // AB.

b) Tính ME, MF theo a, b.

Trả lời

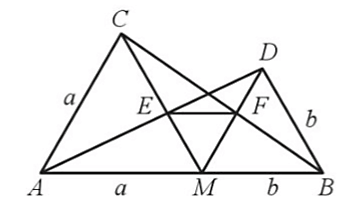
a) Do ∆AMC và ∆BMD là các tam giác đều nên ta có: AC = AM = CM = a, DM = DB = MB = b và $\widehat{DMB}=\widehat{CAM}=60°,$ $\widehat{DBM}=\widehat{CMA}=60°.$

Mà các cặp góc này ở vị trí so le trong nên MD // AC, DB // CM.

Xét ∆ACE với MD // AC, ta có $\frac{EC}{EM}=\frac{AC}{DM}=\frac{a}{b}$ (hệ quả của định lí Thalès).

Xét ∆BDF với DB // CM, ta có $\frac{FC}{FB}=\frac{CM}{DB}=\frac{a}{b}$ (hệ quả của định lí Thalès).

Từ đó, ta có: $\frac{EC}{EM}=\frac{FC}{FB}=\frac{a}{b}$

Xét ∆CMB có $\frac{EC}{EM}=\frac{FC}{FB}$ nên EF // MB hay EF // AB (do M ∈ AB).

b) Từ EF // AB (câu a) suy ra $\widehat{EFM}=\widehat{FMB}=60°,$ $\widehat{FEM}=\widehat{EMA}=60°$ (các cặp góc ở vị trí so le trong)

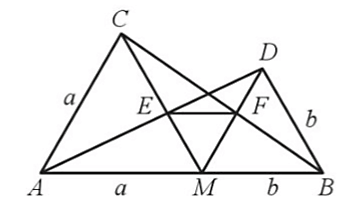
Tam giác EMF có $\widehat{EFM}=\widehat{FEM}=60°$ nên tam giác EMF là tam giác đều.

Do đó ME = MF = EF.

Xét ∆CMB có EF // MB nên ta có: $\frac{CE}{CM}=\frac{EF}{MB}$ (hệ quả của định lí Thalès).

Do đó $\frac{CE}{CM}=\frac{EF}{MB}$ = $\frac{CE+EF}{CM+MB}$ = $\frac{CE+EM}{CM+MB}$ = $\frac{CM}{CM+MB}$ = $\frac{a}{a+b}$

Hay $\frac{EF}{MB}=\frac{a}{a+b},$ suy ra $EF=\frac{a\cdot MB}{a+b}=\frac{ab}{a+b}.$

Vậy $ME=MF=EF=\frac{ab}{a+b}.$

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài 10: Hình đồng dạng trong thực tiễn

Bài tập cuối chương 8