Một chiếc kệ bảy hoa quả có ba tầng được thiết kế như Hình 59. Tầng đáy có đường kính AB là 32 cm

Bài 67 trang 85 SBT Toán 8 Tập 2: Một chiếc kệ bảy hoa quả có ba tầng được thiết kế như Hình 59. Tầng đáy có đường kính AB là 32 cm. Tầng giữa có đường kính CD nhỏ hơn đường kính tầng đáy là 12 cm. Tính độ dài đường kính tầng trên cùng EF, biết EF // AB; D, C lần lượt là trung điểm của EA và FB.

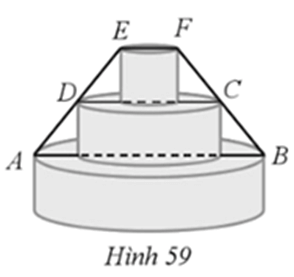
Trả lời

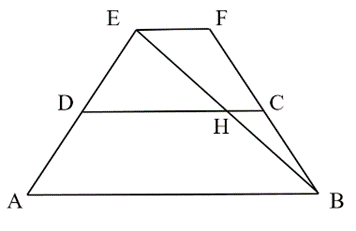
Độ dài đường kính CD là: 32 ‒ 12 = 20 (cm).

Gọi H là trung điểm của EB.

Xét ∆EAB có D, H lần lượt là trung điểm của EA, EB nên DH là đường trung bình của ∆EAB. Do đó DH // AB và $DH=\frac{1}{2}AB.$

Tương tự, HC là đường trung bình của ∆BEF. Do đó HC // EF và $HC=\frac{1}{2}EF.$

Mà EF // AB nên DH // AB, HC // AB

Theo tiên đề Euclid ta có ba điểm D, H, C thẳng hàng.

Khi đó DC // EF // AB.

Xét ∆EAB có DH // AB nên ∆EDH ᔕ ∆EAB.

Suy ra $\frac{DE}{AE}=\frac{DH}{AB}=\frac{1}{2}$ (tỉ số đồng dạng)

Do đó $\text{DH}=\frac{1}{2}AB=\frac{1}{2}\cdot 32=16$ (cm).

Khi đó HC = DC ‒ DH = 20 ‒ 16 = 4 (cm).

Syu ra EF = 2.HC = 2.4 = 8 (cm).

Vậy độ dài đường kính tầng trên cùng EF bằng 8 cm.

Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:

Bài 6: Trường hợp đồng dạng thứ nhất của tam giác

Bài 7: Trường hợp đồng dạng thứ hai của tam giác

Bài 8: Trường hợp đồng dạng thứ ba của tam giác

Bài 9: Hình đồng dạng

Bài 10: Hình đồng dạng trong thực tiễn

Bài tập cuối chương 8