Bài 70 trang 85 SBT Toán 8 Tập 2: Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau tại H. Chứng minh:
a) ∆EBH ᔕ ∆DCH, ∆ADE ᔕ ∆ABC;
b) DB là tia phân giác của góc EDI, với I là giao điểm của AH và BC.
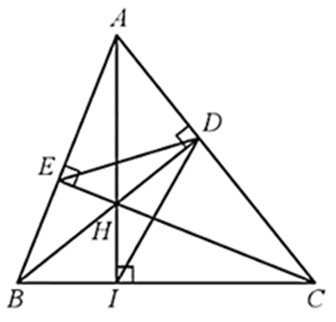
a) Do BD, CE là các đường cao nên BD ⊥ AC, CE ⊥ AB.
Xét ∆EBH và ∆DCH có:
(hai góc đối đỉnh)
Do đó ∆EBH ᔕ ∆DCH (g.g.).
Xét ∆ABD và ∆ACE có:
là góc chung
Do đó ∆ADE ᔕ ∆ABC (g.g).
Suy ra (tỉ số đồng dạng).
Xét ∆ADE và ∆ABC có:
là góc chung
Do đó ∆ADE ᔕ ∆ABC (c.g.c).
b) Do ∆ADE ᔕ ∆ABC (câu a) nên (hai góc tương ứng) (1).
Xét ∆CIA và ∆CDB có:
là góc chung
Do đó ∆CIA ᔕ ∆CDB (g.g).
Suy ra (tỉ số đồng dạng) hay
Xét ∆CDI và ∆CBA có:
là góc chung
Do đó ∆CDI ᔕ ∆CBA (c.g.c).
Suy ra (hai góc tương ứng) (2).
Từ (1) và (2), ta có
Do đó hay .
Vậy DB là đường phân giác của góc EDI.
Xem thêm các bài giải SBT Toán 8 Cánh diều hay, chi tiết khác:
Bài 6: Trường hợp đồng dạng thứ nhất của tam giác
Bài 7: Trường hợp đồng dạng thứ hai của tam giác
Bài 8: Trường hợp đồng dạng thứ ba của tam giác