Giải SBT Toán 8 (Cánh diều) Bài tập cuối chương 5 trang 103

Giải SBT Toán 8 Bài tập cuối chương 5 trang 103

Bài 37 trang 103 SBT Toán 8 Tập 1: Cho hình bình hành $ABCD$ có $\hat{A}=3\hat{B}$. Số đo các góc của hình bình hành $ABCD$ là:

Bài 38 trang 103 SBT Toán 8 Tập 1: Cho hình vuông $ABCD$ có độ dài bằng 8 cm. Độ dài đường chéo $AC$ là:

A.  $4\sqrt{2}cm$

B.  $8\sqrt{2}cm$

C.  $2\sqrt{8}cm$

D.  $4\sqrt{8}cm$

Lời giải:

Xét tam giác vuông cân $ABC$ ta có:

$A{C}^2=A{B}^2+B{C}^2$ suy ra $A{C}^2=8^2+8^2=128$

Vậy độ dài đường chéo $AC=\sqrt{128}=8\sqrt{2}cm$

→  Đáp án đúng là đáp án B.

Bài 39 trang 103 SBT Toán 8 Tập 1: Cho tứ giác $ABCD$ có $E,F,G,H$ lần lượt là trung điểm của $AB,BC,CD,DA$. Điều kiện của tứ giác $ABCD$ để tứ giác $EFGH$ là hình chữ nhật là:

A.  $BD=AC$

B.  $AB\mathrm{\perp }BC$

C.  $BD\mathrm{\perp }AC$

D.  $AB=CD$

Lời giải:

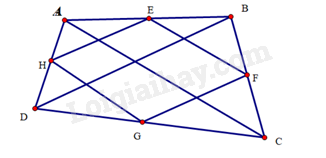
Nối $AC,BD$

Xét tam giác $ABCD$ có $E,H$ lần lượt là trung điểm của $AB,AD$ nên $EH$ là đường trung bình của tam giác $ABD$.

Suy ra $EH//BD,EH=\frac{1}{2}BD$ (1)

Tương tự xét tam giác $CBD$ có $F,G$ lần lượt là trung điểm của $BC,CD$ nên $Fg$ là đường trung bình của tam giác $CBD$ suy ra $FG//BD,FG=\frac{1}{2}BD$ (2)

Từ (1), (2) suy ra $EH//FG;EH=FG$ nên $EFGH$ là hình bình hành (dấu hiệu nhận biết).

Để hình bình hành $EFGH$ là hình chữ nhật thì $\widehat{EHG}={90}^{\circ }$ hay $EH\mathrm{\perp }HG$

Lại có $HG//AC$ (do $HG$ là đường trung bình của tam giác $DAC$) nên $EH\mathrm{\perp }AC$ mà $EH\mathrm{\perp }BD$ (cmt) nên $AC\mathrm{\perp }BD$.

Vậy tứ giác $ABCD$ cần có $AC\mathrm{\perp }BD$ thì $EFGH$ là hình chữ nhật.

→   Đáp án đúng là đáp án C.

Bài 40 trang 103 SBT Toán 8 Tập 1: Một công ti dự định làm một đường ống dẫn từ một nhà máu ở địa điểm $C$ trên bờ đến một địa điểm $B$ trên biển. Khoảng cách giữa địa điểm $A$ trên đảo với địa điểm $B$, địa điểm $C$ lần lượt là $9km$, $15km$; $AB$ vuông góc với $BC$ (minh họa ở Hình 27). Giá làm 1 km đường ống là 5 000 đô la Mỹ. Hỏi chi phí làm đường ống từ địa điểm $C$ đến địa điểm $B$ là bao nhiêu đồng? Biết 1 đô la Mỹ bằng 23 635 đồng.

Lời giải:

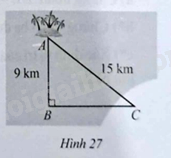
Trong tam giác $ABC$ vuông tại $B$ ta có: $A{C}^2=A{B}^2+B{C}^2$ (theo định lí Pythagore).

Suy ra $B{C}^2=A{C}^2-A{B}^2={15}^2-9^2=144$. Do đó $BC=\sqrt{144}=12\left(km\right)$

Chi phí làm đường ống từ địa điểm $C$ đến địa điểm $B$ là:

$\mathrm{5000.23635.12}=1418100000$ (đồng)

Bài 41 trang 104 SBT Toán 8 Tập 1: Cho tam giác $ABC$ vuông tại $A$ có đường cao $AH$. Kẻ $HJ$ vuông góc với $AB$ tại $J$ và $HK$ vuông góc với $AC$ tại $K$. Trên tia $HJ$ lấy điểm $D$ sao cho $DJ=JH$. Trên tia $HK$ lấy điểm $E$ sao cho $EK=KH$.

a) Chứng minh $A$ là trung điểm của $DE$.

b) Tứ giác $AJHK$ là hình gì? Vì sao?

c) Chứng minh $BC=BD+CE$.

Lời giải:

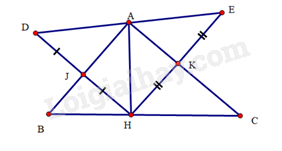
a)  Xét $\mathrm{\Delta }ADJ$ vuông tại $J$ và $\mathrm{\Delta }AHJ$ vuông tại $J$ có:

$DJ=HJ$ (gt), $AJ$ là cạnh chung

Do đó $\mathrm{\Delta }ADJ=\mathrm{\Delta }AHJ$ (hai cạnh góc vuông)

Suy ra $AD=AH$ (hai cạnh tương ứng) và $\widehat{JAD}=\widehat{JAH}$ (hai góc tương ứng)

Tương tự ta cũng chứng minh được $\mathrm{\Delta }AHK=\mathrm{\Delta }AEk$ (hai cạnh góc vuông)

Suy ra $AH=AE$ (hai cạnh tương ứng) và $\widehat{KAH}=\widehat{KAE}$ (hai góc tương ứng)

Ta có:

$\widehat{JAD}+\widehat{JAH}+\widehat{KAH}+\widehat{KAE}=2\left(\widehat{JAH}+\widehat{KAH}\right)=2.\widehat{JAK}={2.90}^{\circ }={180}^{\circ }$

Hay $\widehat{DAE}={180}^{\circ }$ nên ba điểm $D,A,E$ thẳng hàng

Lại có $AD=AH$ và $AH=AE$ nên $AD=AE$

Do đó $A$ là trung điểm của $DE$.

b) Ta có $AB\mathrm{\perp }HE$ tại $K$ nên $\widehat{AJH}={90}^{\circ }$

$AC\mathrm{\perp }HE$ tại $K$ nên $\widehat{AKH}={90}^{\circ }$

Xét tứ giác $AJKH$ có:

$\widehat{AJH}=\widehat{JAK}=\widehat{AKH}={90}^{\circ }$ nên là hình chữ nhật.

c) Xét tam giác $BDJ$ vuông tại $J$ và tam giác $BHJ$ vuông tại $J$ có:

$DJ=HJ$ (gt), $BJ$ là cạnh chung

Do đó $\mathrm{\Delta }BDJ=\mathrm{\Delta }BHJ$ (hai cạnh góc vuông)

Suy ra $BD=BH$ (hai cạnh tương ứng)

Tương tự, ta cũng có $\mathrm{\Delta }CHK=\mathrm{\Delta }CEK$ (hai cạnh góc vuông)

Suy ra $CH=CE$ (hai cạnh tương iwnsg)

Khi đó $BC=BH+CH=BD+CE$

Vậy $BC=BD+CE$.

Bài 42 trang 104 SBT Toán 8 Tập 1: Cho hình thang cân $ABCD$ có $AB//CD,\hat{D}={45}^{\circ }$. Kẻ $AH$ vuông góc với $CD$ tại $H$. Lấy điểm $E$ thuộc cạnh $CD$ sao cho $HE=DH$.

a) Chứng minh tứ giác $ABCE$ là hình bình hành.

b) Đường thẳng qua $D$ song song với $AE$ cắt $AH$ tại $F$. Tứ giác $ADFE$ là hình gì? Vì sao?

c) Tìm điều kiện của hình thang cân $ABCD$ để $E$ là trung điểm của $BF$ (bỏ qua giả thiết $\hat{D}={45}^{\circ }$).

Lời giải:

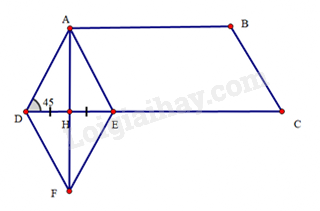
a) $\mathrm{\Delta }ADH=\mathrm{\Delta }AEH$ (cạnh góc vuông – cạnh góc vuông), suy ra $AD=AE$ (hai cạnh tương ứng)

Xét tứ giác $ABCE$, ta có:

$AB//EC$

Vì $AD=AE$ mà $AD=BC$ nên $AE=BC$

Vậy tứ giác $ABCE$ là hình bình hành.

b) Xét tam giác $AHE$ và $FHD$, ta có:

$\widehat{AEH}=\widehat{FDH}$ (so le trong); $\widehat{AHE}=\widehat{FHD}={90}^{\circ }$; $DH=HE$

Suy ra $\mathrm{\Delta }AHE=\mathrm{\Delta }DHD$ (g.c.g)

Suy ra $AH=HF$

Xét tứ giác $ADEF$, ta có:

$HD=HE;HA=HF$

Mà $AF\mathrm{\perp }DE$

Suy ra tứ giác $ADEF$ là hình thoi.

c)  Để $E$ là trung điểm của $BF$ thì $BE=FE$ và ba điểm $B,E,F$ thẳng hàng.

Khi bỏ qua giả thiết $\widehat{ADC}={45}^{\circ }$ thì ta chứng minh được tứ giác $ADEF$ có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên $ADEF$ là hình bình hành.

Do $ABCE$ và $ADEF$ đều là hình bình hành nên $AE=BC,AE//BC$ và $AE=DF.AE//DF$

Suy ra $BC=DF$ và $BC//DF$

Tứ giác $BCFD$ có $BC=DF$ và $BC//DF$ nên $BCFD$ là hình bình hành.

Mà $E$ là trung điểm của $BF$, suy ra $E$ là trung điểm của $CD$ hay $EC=ED=\frac{1}{2}CD$.

Mặt khác, $AB=EC$ (vì $ABCE$ là hình bình hành), suy ra $AB=\frac{1}{2}CD$

Dễ thấy nếu hình thang cân $ABCD\left(AB//CD\right)$ có $AB=\frac{1}{2}CD$ thì $E$ là trung điểm của $BF$.

Vậy điều kiện của hình thang cân $ABCD\left(AB//CD\right)$ để $E$ là trung điểm của $BF$ là $AB=\frac{1}{2}CD$.

Bài 43 trang 104 SBT Toán 8 Tập 1: Cho hình bình hành $ABCD$ có $BC=2AB$. Gọi $M,N$ lần lượt là trung điểm của $BC,AD$

a) Chứng minh tứ giác $MBND$ là hình bình hành.

b) Gọi $P$ là giao điểm của $AM$ và $BN,Q$ là giao điểm của $CN$ và $DM$. Chứng minh tứ giác $PMQN$ là hình chữ nhật.

c) Tìm điều kiện của hình bình hành $ABCD$ để tứ giác $PMQN$ là hình vuông.

d) Tính diện tích của tứ giác $PMQN$, biết $AB=2cm,\widehat{MAD}={30}^{\circ }$.

Lời giải:

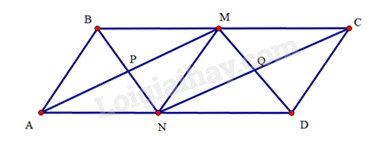
a) Do $ABCD$ là hình bình hành nên $BC//AD$ và $BC=AD$

Mà $M\in BC,N\in AD$ nên $MB//ND$

Lại có $M,N$ lần lượt là trung điểm của $BC,AD$ nên $MB=MC=\frac{1}{2}BC,NA=ND=\frac{1}{2}A$

Do đó $MB=MC=NA=ND$

Tứ goác $MBND$ có $MB//ND$ và $MB=ND$ nên là hình bình hành.

b) Tương tự câu a, ta chứng minh được $MANC$ là hình bình hành.

Do $MBND,MANC$ đều là hình bình hành nên $PN//MQ,PM//NQ$. Suy ra tứ giác $PMQN$ là hình bình hành.

$\mathrm{\Delta }ABN=\mathrm{\Delta }MBN$ (c.g.c). Suy ra $AB=MN$.

Tứ giác $ABMN$ có $AB=BM-MN=AN$ nên $ABMN$ là hình thoi. Suy ra $AM\mathrm{\perp }Bn$

Hình bình hành $PMQN$ có $\widehat{MPN}={90}^{\circ }$ nên $PMQN$ là hình chữ nhật.

c) Để hình chữ nhật $PMQN$ là hình vuông thì $PM=PN$.

Mà $ABMN$ là hình thoi nên $ABMN$ là hình bình hành. Suy ra $AM,BN$ cắt nhau tại trung điểm $P$ của mỗi đường. mà $PM=PN$, suy ra $AM=BN$

Hình bình hành $ABMN$ có $AM=BN$ nên $ABMN$ là hình chữ nhật

Suy ra $\widehat{ABM}={90}^{\circ }$ hay $\widehat{ABC}={90}^{\circ }$

Hình bình hành $ABCD$ có $\widehat{ABC}={90}^{\circ }$ nên $ABCD$ là hình chữ nhật.

Dễ thấy, nếu hình bình hành $ABCD$ là hình chữ nhật và $BC=2AB$ thì $PMQN$ là hình vuông.

Vậy điều kiện của hình bình hành $ABCD$ để $PMQN$ là hình vuông là hình bình hành $ABCD$ là hình chữ nhật có $BC=2AB$.

d) Ta có: $BM=AB$ nên $BM=2cm$

Do $ABMN$ là hình thoi nên $AM$ là tia phân giác của $\widehat{BAN}$

Suy ra $\widehat{BAN}=2\widehat{MAD}={60}^{\circ }$

Tam giác $ABN$ có $AB=AN$ và $\widehat{BAN}={60}^{\circ }$ nên tam giác $ABN$ đều.

Suy ra $BN=AN=AB=2cm$

Do $P$ là trung điểm của $BN$ nên $BP=NP=\frac{BN}{2}=1cm$

Trong tam giác $BMP$ vuông tại $P$, ta có: $B{M}^2=B{P}^2+M{P}^2$

Suy ra $M{P}^2=B{M}^2-B{P}^2=3$. Do đó $MP=\sqrt{3}$ cm

Do $PMQN$ là hình chữ nhật nên diện tích của $PMQN$ là:

$MP.NP=\sqrt{3}.1=\sqrt{3}\left(c{m}^2\right)$.

Bài 44 trang 104 SBT Toán 8 Tập 1: Cho hình vuông $ABCD$. Lấy điểm $M$ thuộc đường chéo $BD$. Kẻ $ME$ vuông góc với $AB$ tại $E$,$MF$ vuông góc với $AD$ tại $F$.

a) Chứng minh: $DE=CF;DE\mathrm{\perp }CF$.

b) Chứng minh ba đường thẳng $DE,BF,CM$ cùng đi qua một điểm.

c) Xác định vị trí của điểm $M$ trên đường chéo $BD$ để diện tích của tứ giác $AEMF$ lớn nhất.

Lời giải:

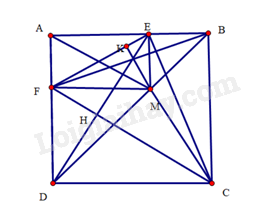
Gọi $H$ là giao điểm của $DE$ và $CF$, $K$ là giao điểm của $CM$ và $EF$.

Do $ABCD$ là hình vuông nên ta có:

$\widehat{DAB}={90}^{\circ },CD=DA,\widehat{ADB}=\widehat{ABD}=\widehat{DBC}={45}^{\circ }$

a) Ta chứng minh được tam giác $FDM$ vuông cân tại $F$.

Suy ra $FM=DF$

Tứ giác $AEMF$ có $\widehat{MFA}=\widehat{FAE}=\widehat{AEM}={90}^{\circ }$ nên $AEMF$ là hình chữ nhật. Suy ra $AE=FM$.

Do đó $AE=DF$ (vì cùng bằng $FM$)

$\mathrm{\Delta }ADE=\mathrm{\Delta }DCF$ (c.g.c). Suy ra $DE=CF$, $\widehat{AED}=\widehat{DFC}$.

Trong tam giác $ADE$ vuông tại $A$, ta có: $\widehat{AED}+\widehat{ADE}={90}^{\circ }$

Suy ra $\widehat{DFC}+\widehat{ADE}={90}^{\circ }$ hay $\widehat{DFH}+\widehat{FHD}={90}^{\circ }$. Từ đó ta tính được $\widehat{DHF}={90}^{\circ }$. Vậy $DE\mathrm{\perp }CF$.

b) Tương tự câu a, ta chứng minh được $BF\mathrm{\perp }CE$.

$\mathrm{\Delta }ABM=\mathrm{\Delta }CBM$ (c.g.c). Suy ra $AM=CM$. Mà $EF=AM$ (vì $AEMF$ là hình chữ nhật) suy ra $EF=CM$.

$\mathrm{\Delta }DEF=\mathrm{\Delta }FCM$ (c.c.c). Suy ra $\widehat{DEF}=\widehat{FCM}$ hay $\widehat{FEH}=\widehat{FCK}$

Trong tam giác $HEF$ vuông tại $H$, ta có $\widehat{FEH}+\widehat{EFH}={90}^{\circ }$

Suy ra $\widehat{FCK}+\widehat{EFH}={90}^{\circ }$ hay $\widehat{FCK}+\widehat{KFC}={90}^{\circ }$. Từ đó, ta tính được $\widehat{CKF}={90}^{\circ }$. Do đó, $CK\mathrm{\perp }EF$.

Trong tam giác $CEF$, ta có: $DE\mathrm{\perp }CF,BF\mathrm{\perp }CE,CM\mathrm{\perp }EF$ nên ba đường thẳng $DE,BF,CM$ là các đường cao của tam giác $CEF$. Vậy ba đường thẳng $DE,BF,CM$ cùng đi qua một điểm.

c) Chu vi của hình chữ nhật $AEMF$ là: $2\left(AE+AF\right)=2\left(DF+AF\right)=2AD$

Mà $AD$ không đổi nên chu vi của hình chữ nhật $AEMF$ không đổi. Do đó, diện tích của tứ giác $AEMF$ lớn nhất khi $AEMF$ là hình vuông. Suy ra $ME=MF$.

Khi đó $\mathrm{\Delta }BEM=\mathrm{\Delta }DFM$ (cạnh góc vuông – góc nhọn kề). Suy ra $BM=DM$ hay $M$ là trung điểm của $BC$

Vậy với $M$ là trung điểm của $BC$ thì diện tích của tứ giác $AEMF$ lớn nhất.

Xem thêm Lời giải bài tập Toán 8 sách Cánh diều hay, chi tiết khác:

Bài 6: Hình thoi

Bài 7: Hình vuông

Bài 1: Đơn thức nhiều biến. Đa thức nhiều biến

Bài 2: Các phép tính với đa thức nhiều biến

Bài 3: Hằng đẳng thức đáng nhớ