Giải SBT Toán 11 (Chân trời sáng tạo) Bài tập cuối chương 3 trang 91

Sách bài tập Toán 11 Bài tập cuối chương 3 trang 91

A. TRẮC NGHIỆM

Câu 1 trang 91 SBT Toán 11 Tập 1: $\text{lim}\frac{3n^2+2n}{2-n^2}$ bằng

A. $\frac{3}{2}.$

B. ‒2.

C. 3.

D. ‒3.

Lời giải:

Đáp án đúng là: D

Ta có: $\text{lim}\frac{3n^2+2n}{2-n^2}=\lim \frac{3+\frac{2}{n}}{\frac{2}{n^2}-1}=\frac{3}{-1}=-3.$

Câu 2 trang 92 SBT Toán 11 Tập 1: Ta có: $\text{lim}\frac{\sqrt{4n^2+4n+1}}{4n+1}$ bằng

A. $\frac{1}{2}.$

B. 1.

C. 2.

D. +∞.

Lời giải:

Đáp án đúng là: A

$\text{lim}\frac{\sqrt{4n^2+4n+1}}{4n+1}=\lim \frac{\sqrt{4+\frac{4}{n}+\frac{1}{n^2}}}{4+\frac{1}{n}}=\frac{\sqrt{4}}{4}=\frac{1}{2}.$

Câu 3 trang 92 SBT Toán 11 Tập 1: $\text{lim}\frac{2n+1}{\sqrt{9n^2+1}-n}$ bằng

A. $\frac{2}{3}.$

B. 1.

C. $\frac{1}{4}.$

D. 2.

Lời giải:

Đáp án đúng là: B

$\text{lim}\frac{2n+1}{\sqrt{9n^2+1}-n}=\lim \frac{2+\frac{1}{n}}{\sqrt{9+\frac{1}{n^2}}-1}=\frac{2}{3-1}=1.$

Câu 4 trang 92 SBT Toán 11 Tập 1: Cho hai dãy số (u_n) và (v_n) thoả mãn limu_n = 4, lim(v_n – 3) = 0.

lim[u_n(u_n – v_n)] bằng

A. 7.

B. 12.

C. 4.

D. 28.

Lời giải:

Đáp án đúng là: C

Ta có lim(v_n ‒ 3) = 0⇔ limv_n = 3

Khi đó $\text{lim}\left(u_n\left(u_n-v_n\right)\right)=\lim \left(u_n^2-u_n{v}_n\right)=4^2-\left(4\cdot 3\right)=4.$

Câu 5 trang 92 SBT Toán 11 Tập 1: $\text{lim}\frac{4^n}{2\cdot 4^n+3^n}$ bằng

A. $\frac{1}{2}.$

B. 1.

C. 4.

D. 0.

Lời giải:

Đáp án đúng là: A

Ta có: $\text{lim}\frac{4^n}{2\cdot 4^n+3^n}=\lim \frac{1}{2+{\left(\frac{3}{4}\right)}^n}=\frac{1}{2}.$

Câu 6 trang 92 SBT Toán 11 Tập 1: $\underset{x\to 2}{\lim }\frac{x^2-x-2}{2x-4}$ bằng

A. $\frac{3}{2}.$

B. $\frac{1}{2}.$

C. 1.

D. $-\frac{1}{2}.$

Lời giải:

Đáp án đúng là: A

Ta có $\underset{x\to 2}{\lim }\frac{x+1}{2}=\underset{x\to 2}{\lim }\frac{\left(x-2\right)\left(x+1\right)}{2\left(x-2\right)}$$=\underset{x\to 2}{\lim }\frac{x+1}{2}=\frac{2+1}{2}=\frac{3}{2}.$

Câu 7 trang 92 SBT Toán 11 Tập 1: $\underset{x\to 1}{\lim }\frac{2x-2}{\sqrt{x+3}-2}$ bằng

A. 0.

B. +∞.

C. 2.

D. 8.

Lời giải:

Đáp án đúng là: D

Ta có $\frac{2x-2}{\sqrt{x+3}-2}=\frac{\left(2x-2\right)\left(\sqrt{x+3}+2\right)}{\left(x+3-4\right)}$

$=\frac{2\left(x-1\right)\left(\sqrt{x+3}+2\right)}{x-1}=2\left(\sqrt{x+3}+2\right).$

Khi đó $\underset{x\to 1}{\lim }\frac{2x-2}{\sqrt{x+3}-2}=\underset{x\to 1}{\lim }\left(2\left(\sqrt{x+3}+2\right)\right)$ $=2\cdot \left(\sqrt{1+3}+2\right)=8.$

Câu 8 trang 92 SBT Toán 11 Tập 1: Biết $\underset{x\to 1}{\lim }\frac{x^2-3x+a}{x-1}=b$ với a và b là hai số thực. Giá trị của a + b bằng

A. 1.

B. 2.

C. 4.

D. 5.

Lời giải:

Đáp án đúng là: A

Do $\underset{x\to 1}{\lim }\left(x-1\right)=0$ nên để tồn tại giới hạn hữu hạn $\underset{x\to 1}{\lim }\frac{x^2-3x+a}{x-1}=b,$ trước hết ta phải

có $\underset{x\to 1}{\lim }\left(x^2-3x+a\right)=0$ hay 1² ‒ 3.1 + a = 0 ⇔ a = 2.

Khi đó, $\underset{x\to 1}{\text{lim}}\frac{x^2-3x+a}{x-1}=\underset{x\to 1}{\text{lim}}\frac{x^2-3x+2}{x-1}$

$\underset{x\to 1}{\text{lim}}\frac{\left(x-1\right)\left(x-2\right)}{x-1}=\underset{x\to 1}{\text{lim}}\left(x-2\right)=1-2=-1$

Theo bài, $\underset{x\to 1}{\lim }\frac{x^2-3x+a}{x-1}=b$ nên b = −1.

Suy ra a + b = 2 + (‒1) = 1.

Câu 9 trang 92 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{x^2-3x}{\left|x-3\right|}.$ Đặt $a=\underset{x\to 3^{+}}{\lim }f\left(x\right)$ và $b=\underset{x\to 3^{-}}{\lim }f\left(x\right).$ Giá trị của a ‒ 2b bằng

A. 0.

B. 9.

C. ‒3.

D. ‒9.

Lời giải:

Đáp án đúng là: B

Ta có:

$a=\underset{x\to 3^{+}}{\lim }f\left(x\right)=\underset{x\to 3^{+}}{\lim }\frac{x^2-3x}{\left|x-3\right|}=\underset{x\to 3^{+}}{\lim }\frac{x^2-3x}{x-3}=\underset{x\to 3^{+}}{\lim }x=3.$

$b=\underset{x\to 3^{-}}{\lim }f\left(x\right)=\underset{x\to 3^{-}}{\lim }\frac{x^2-3x}{\left|x-3\right|}=\underset{x\to 3^{-}}{\lim }\frac{x^2-3x}{3-x}=\underset{x\to 3^{-}}{\lim }\left(-x\right)=-3.$

Khi đó a ‒ 2b = 3 ‒ 2.(‒3) = 9.

Câu 10 trang 92 SBT Toán 11 Tập 1: Biết rằng $\underset{x\to +\infty }{\lim }f\left(x\right)=2,\underset{x\to +\infty }{\lim }\left(f\left(x\right)+2g\left(x\right)\right)=4$. Giới hạn $\underset{x\to +\infty }{\lim }\frac{f\left(x\right)-2g\left(x\right)}{f\left(x\right)+2g\left(x\right)}$ bằng

A. ‒1.

B. 0.

C. $\frac{1}{2}$

D. $-\frac{1}{2}$

Lời giải:

Đáp án đúng là: B

$\underset{x\to +\infty }{\lim }\left(f\left(x\right)+2g\left(x\right)\right)=4$

$\iff \underset{x\to +\infty }{\lim }f\left(x\right)+2\underset{x\to +\infty }{\lim }g\left(x\right)=4$

$\iff 2\underset{x\to +\infty }{\lim }g\left(x\right)=4-2=2$

Suy ra $\underset{x\to +\infty }{\lim }\frac{f\left(x\right)-2g\left(x\right)}{f\left(x\right)+2g\left(x\right)}=\frac{\underset{x\to +\infty }{\lim }f\left(x\right)-2\underset{x\to +\infty }{\lim }g\left(x\right)}{\underset{x\to +\infty }{\lim }f\left(x\right)+2\underset{x\to +\infty }{\lim }g\left(x\right)}=\frac{2-2}{2+2}=0.$

Câu 11 trang 93 SBT Toán 11 Tập 1: Biết rằng $\underset{x\to +\infty }{\lim }\frac{2\mathrm{ax}}{\sqrt{x^2+\mathrm{ax}}+x}=3.$ Giá trị của a là

A. $\frac{3}{4}$

B. 6.

C. $\frac{3}{2}$

D. 3.

Lời giải:

Đáp án đúng là: D

Ta có $\underset{x\to +\infty }{\lim }\frac{2ax}{\sqrt{x^2+ax}+x}=3\iff \underset{x\to +\infty }{\lim }\frac{2a}{\sqrt{1+\frac{a}{x}}+1}=3$

$\iff \frac{2a}{2}=3\iff a=3.$

Câu 12 trang 93 SBT Toán 11 Tập 1: $\underset{x\to -2^{-}}{\lim }\frac{1-3x}{x+2}$ bằng

A. +∞.

B. ‒∞.

C. ‒3 .

D. $\frac{7}{4}$

Lời giải:

Đáp án đúng là: B

Do $\underset{x\to -2^{-}}{\lim }\left(1-3x\right)=1-3\cdot \left(-2\right)=1+6=7;\underset{x\to -2^{-}}{\lim }\frac{1}{x+2}=-\infty$

Nên $\underset{x\to -2^{-}}{\lim }\frac{1-3x}{x+2}=\underset{x\to -2^{-}}{\lim }\left(\left(1-3x\right)\cdot \frac{1}{x+2}\right)=-\infty .$

Câu 13 trang 93 SBT Toán 11 Tập 1: Biết rằng hàm số $f\left(x\right)=\left\{\begin{array}{cc}\frac{2-\sqrt{x+1}}{x-3}& \text{ khi }x\ne 3\\ a& \text{ khi }x=3\end{array}\right.$ liên tục tại điểm x = 3. Giá trị của a bằng

A. $-\frac{1}{4}$

B. $\frac{1}{4}$

C. ‒2.

D. 3.

Lời giải:

Đáp án đúng là: A

Hàm số $f\left(x\right)=\frac{2-\sqrt{x+1}}{x-3}$ là hàm số phân thức có tập xác định D = ℝ∖{3} nên nó liên tục trên khoảng (‒∞; 3) và (3; +∞)

Do đó, để hàm số liên tục tại điểm x = 3 thì:

$\underset{x\to 3}{\lim }f\left(x\right)=f\left(3\right)$ hay $\underset{x\to 3}{\lim }\frac{2-\sqrt{x+1}}{x-3}=a$

$\iff \underset{x\to 3}{\lim }\frac{\left(2-\sqrt{x+1}\right)\left(2+\sqrt{x+1}\right)}{\left(x-3\right)\left(2+\sqrt{x+1}\right)}=a$

$\iff \underset{x\to 3}{\lim }\frac{3-x}{\left(x-3\right)\left(2+\sqrt{x+1}\right)}=a$

$\iff \underset{x\to 3}{\lim }\frac{-1}{2+\sqrt{x+1}}=a$

$\iff \frac{-1}{2+\sqrt{3+1}}=a\iff a=\frac{-1}{4}.$

Câu 14 trang 93 SBT Toán 11 Tập 1: Cho hàm số $f\mathrm{(x)} =\left\{\begin{array}{l}\tan x khi 0 \le x\le \frac{\mathrm{\pi }}{4}\\ k-cotx khi \frac{\mathrm{\pi }}{4}<x\le \frac{\mathrm{\pi }}{2}\end{array}\right.$ liên tục trên đoạn $\left[0;\frac{\pi }{2}\right].$ Giá trị của k bằng:

A. 0.

B. 1.

C. 2.

D. $\frac{\pi }{2}.$

Lời giải:

Đáp án đúng là: C

− Hàm số y = tanx là hàm lượng giác có tập xác định $D=ℝ\backslash \left\{\frac{\pi }{2}+\mathrm{k\pi }\right\}$ với k ∈ ℤ nên nó liên tục trên các khoảng $\left(\frac{\pi }{2}+\mathrm{k\pi };\frac{\pi }{2}+\left(k+1\right)\pi \right)$

Mà $\left(0;\frac{\pi }{4}\right)\subset \left(\frac{\pi }{2}+\mathrm{k\pi };\frac{\pi }{2}+\left(k+1\right)\pi \right)$ nên hàm số y = tanx liên tục trên khoảng $\left(0;\frac{\pi }{4}\right)$

− Hàm số y = k – cotx là hàm lượng giác có tập xác định D = ℝ \ {kπ} với với k ∈ ℤ nên nó liên tục trên các khoảng (kπ; (k + 1)π).

Mà $\left(\frac{\pi }{4};\frac{\pi }{2}\right)\subset \left(\mathrm{k\pi };\left(k+1\right)\pi \right)$ nên hàm số y = k – cotx liên tục trên khoảng $\left(\frac{\pi }{4};\frac{\pi }{2}\right).$

− Do đó, để hàm số liên tục trên đoạn $\left[0;\frac{\pi }{2}\right]$ thì hàm số liên tục tại điểm $x=\frac{\pi }{4}$ và $\underset{x\to 0^{+}}{\lim }f\left(x\right)=f\left(0\right),\underset{x\to {\left(\frac{\pi }{2}\right)}^{-}}{\lim }f\left(x\right)=f\left(\frac{\pi }{2}\right).$

⦁ Hàm số liên tục tại điểm $x=\frac{\pi }{4}$ khi và chỉ khi $\underset{x\to {\left(\frac{\pi }{4}\right)}^{-}}{\lim }f\left(x\right)=\underset{x\to {\left(\frac{\pi }{4}\right)}^{+}}{\lim }f\left(x\right)=f\left(\frac{\pi }{4}\right)$

$\iff \tan \frac{\pi }{4}=k-\cot \frac{\pi }{4}=k-\cot \frac{\pi }{4}\iff k-1=1\iff k=2\left(1\right)$

⦁ $\underset{x\to 0^{+}}{\lim }f\left(x\right)=f\left(0\right)\iff \underset{x\to 0^{+}}{\lim }\mathrm{tanx}=\tan 0\iff \tan 0=\tan 0$ (luôn đúng)

⦁ $\underset{x\to {\left(\frac{\pi }{2}\right)}^{-}}{\lim }f\left(x\right)=f\left(\frac{\pi }{2}\right)\iff \underset{x\to {\left(\frac{\pi }{2}\right)}^{-}}{\lim }\left(k-\text{cot}x\right)$

$=k-\text{cot}\frac{\pi }{2}\iff k-\text{cot}\frac{\pi }{2}=k-\text{cot}\frac{\pi }{2}$ (luôn đúng)

Vậy k = 2.

Câu 15 trang 93 SBT Toán 11 Tập 1: Biết rằng phương trình x³ ‒ 2x ‒3 = 0 chỉ có một nghiệm. Phương trình này có nghiệm trong khoảng nào sau đây?

A. (‒1; 0).

B. (0; 1).

C. (1; 2).

D. (2; 3).

Lời giải:

Đáp án đúng là: C

Xét hàm số f(x) = x³ ‒ 2x ‒3 liên tục trên ℝ.

f(‒1) = (‒1)³ ‒ 2.(‒1) ‒ 3 = ‒2.

f(0) = 0³ ‒ 2.0 ‒ 3 = ‒ 3.

f(1) = 1³ ‒ 2.1 ‒ 3 = ‒4.

f(2) = 2³ ‒ 2.2 ‒ 3 = 1.

f(3) = 3³ ‒ 2.3 ‒ 3 = 18.

Ta thấy f(1).f(2) < 0 nên hàm số có nghiệm trong các khoảng (1; 2).

B. TỰ LUẬN

Bài 1 trang 93 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\text{lim}\frac{n\left(2n^2+3\right)}{4n^3+1}$;

b) $\text{lim}\left(\sqrt{n}\left(\sqrt{n+5}-\sqrt{n+1}\right)\right)$.

Lời giải:

a) $\text{lim}\frac{n\left(2n^2+3\right)}{4n^3+1}=\lim \frac{2n^3+3n}{4n^3+1}=\lim \frac{2+\frac{3}{n^2}}{4+\frac{1}{n^3}}=\frac{2}{4}=\frac{1}{2}.$

b) Ta có:

$\sqrt{n}\left(\sqrt{n+5}-\sqrt{n+1}\right)$

$=\frac{\sqrt{n}\left(\sqrt{n+5}-\sqrt{n+1}\right)\left(\sqrt{n+5}+\sqrt{n+1}\right)}{\sqrt{n+5}+\sqrt{n+1}}$

$=\frac{4\sqrt{n}}{\sqrt{n+5}+\sqrt{n+1}}$

Suy ra $\lim \frac{4\sqrt{n}}{\sqrt{n+5}+\sqrt{n+1}}=\lim \frac{4}{\sqrt{1+\frac{5}{n}}+\sqrt{1+\frac{1}{n}}}$ $=\frac{4}{1+1}=2.$

Bài 2 trang 93 SBT Toán 11 Tập 1: Cho các dãy số (u_n) và (v_n) thoả mãn limu_n = 2, lim(u_n – v_n) = 4. Tìm $\text{lim}\frac{3u_n-v_n}{u_n{v}_n+3}.$

Lời giải:

Ta có lim(u_n – v_n) = 4

Suy ra limu_n – limv_n­ = 4, hay limv_n = limu_n – 4 = 2 – 4 = −2.

Do đó $\text{lim}\frac{3u_n-v_n}{u_n{v}_n+3}=\frac{3\text{lim}{u}_n-\text{lim}{v}_n}{\text{lim}{u}_n\cdot \text{lim}{v}_n+3}=\frac{3\cdot 2-\left(-2\right)}{2\cdot \left(-2\right)+3}=-8.$

Bài 3 trang 93 SBT Toán 11 Tập 1: Tìm $\lim \frac{6^n+4^n}{\left(2^n+1\right)\left(3^n+1\right)}$.

Lời giải:

Ta có $\frac{6^n+4^n}{\left(2^n+1\right)\left(3^n+1\right)}=\frac{1+{\left(\frac{2}{3}\right)}^n}{\left(1+\frac{1}{2^n}\right)\left(1+\frac{1}{3^n}\right)}$ (chia cả tử và mẫu cho 6ⁿ = 2ⁿ.3ⁿ).

Do đó $\text{lim}\frac{6^n+4^n}{\left(2^n+1\right)\left(3^n+1\right)}=\lim \frac{1+{\left(\frac{2}{3}\right)}^n}{\left(1+\frac{1}{2^n}\right)\left(1+\frac{1}{3^n}\right)}=\frac{1}{1\cdot 1}=1.$

Bài 4 trang 94 SBT Toán 11 Tập 1: Cho a > b > 0 và $\text{lim}\frac{a^{n+1}+b^n}{2a^n+b^{n+1}}=1.$ Tìm giá trị của a.

Lời giải:

Ta có $\frac{a^{n+1}+b^n}{2a^n+b^{n+1}}=\frac{a+{\left(\frac{b}{a}\right)}^n}{2+b\cdot {\left(\frac{b}{a}\right)}^n}$ (chia cả tử và mẫu cho aⁿ).

Do đó $\text{lim}\frac{a^{n+1}+b^n}{2a^n+b^{n+1}}=\lim \frac{a+{\left(\frac{b}{a}\right)}^n}{2+b{\left(\frac{b}{a}\right)}^n}=\frac{a+0}{2+b\cdot 0}=\frac{a}{2}$

Theo bài, $\text{lim}\frac{a^{n+1}+b^n}{2a^n+b^{n+1}}=1,$ suy ra $\frac{a}{2}=1$, do đó a = 2.

Bài 5 trang 94 SBT Toán 11 Tập 1: Cho dãy số (u_n) thoả mãn ${\mathrm{limnu}}_n=\frac{1}{2}.$ Tìm lim(3n – 4)u_n.

Lời giải:

Ta có $\text{lim}{u}_n=\text{lim}\left(\frac{1}{n}\cdot {\mathrm{nu}}_n\right)=\text{lim}\frac{1}{n}\cdot \text{lim}{\mathrm{nu}}_n=0\cdot \frac{1}{2}=0$.

Từ đó:

$\text{lim}\left(3n-4\right)u_n=\text{lim}\left(3{\mathrm{nu}}_n-4u_n\right)$$=3{\mathrm{limnu}}_n-4\text{lim}{u}_n=3\cdot \frac{1}{2}-4\cdot 0=\frac{3}{2}$.

Bài 6 trang 94 SBT Toán 11 Tập 1: Từ một tam giác đều có diện tích bằng 1, ta thực hiện lần lượt các bước như sau:

Bước 1: Nối trung điểm các cạnh của tam giác đã cho, chia tam giác này thành 4 tam giác nhỏ và bỏ đi tam giác ở giữa (bỏ đi 1 tam giác có diện tích $\frac{1}{4}$).

Bước 2: Làm tương tự như Bước 1 với mỗi tam giác trong 3 tam giác còn lại (bỏ đi 3 tam giác, mỗi tam giác có diện tích $\frac{1}{4^2}$).

Cứ tiếp tục quá trình như vậy (ở bước thứ n, bỏ đi 3^n‒1 tam giác, mỗi tam giác diện tích $\frac{1}{4^n}$). Tính tổng diện tích các tam giác đã bỏ đi.

Lời giải:

Ta có:

$S=\frac{1}{4}+3\cdot {\left(\frac{1}{4}\right)}^2+3^2\cdot {\left(\frac{1}{4}\right)}^3+\dots +3^n\cdot {\left(\frac{1}{4}\right)}^{n+1}+\dots$

$=\frac{1}{4}+\frac{1}{4}\cdot \frac{3}{4}+\frac{1}{4}\cdot {\left(\frac{3}{4}\right)}^2+\dots +\frac{1}{4}\cdot {\left(\frac{3}{4}\right)}^n+\dots$

Đây là tổng cấp số nhân lùi vô hạn với số hạng đầu $u_1=\frac{1}{4},$ công bội $q=\frac{3}{4}$ thỏa mãn |q| < 1 nên $S=\frac{1}{4}\cdot \frac{1}{1-\frac{3}{4}}=1$.

Bài 7 trang 94 SBT Toán 11 Tập 1: Biết rằng, từ vị trí A, một mũi tên bay với tốc độ 10m/s hướng thẳng tới bia mục tiêu đặt ở vị trí B cách vị trí A một khoảng bằng 10m (Hình 2). Một nhà thông thái lập luận như sau: “Để đến được B, trước hết mũi tên phải đến trung điểm A₁ của AB. Tiếp theo, nó phải đến trung điểm A₂ của A₁B. Tiếp nữa, nó phải đến trung điểm A₃ của A₂B. Cứ tiếp tục như vậy, vì không bao giờ hết các trung điểm nên mũi tên không thể bay đến được bia mục tiêu ở B”.

Lập luận trên có đúng không? Nếu không, hãy chỉ ra chỗ sai lầm.

Lời giải:

Thời gian để mũi tên bay từ A đến A₁ là giây, từ A₁ đến A₂ là $\frac{1}{4}=\frac{1}{2^2}$ giây, từ A₂ đến A₃ là $\frac{1}{8}=\frac{1}{2^3}$ giây, …

Tổng thời gian bay của mũi tên là $\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\dots +\frac{1}{2^n}+\dots \left(*\right)$

Đây là tổng của cấp số nhân lùi vô hạn với số hạng đầu là $u_1=\frac{1}{2}$ và công bội bằng $q=\frac{1}{2}$ thỏa mãn |q| < 1.

Do đó, tổng này bằng $\frac{1}{2}\cdot \frac{1}{1-\frac{1}{2}}=1$ (giây).

Như vậy, mũi tên đến bia mục tiêu sau 1 giây.

Lập luận của nhà thông thái không đúng, sai lầm ở chỗ cho rằng tổng ở (*) không phải là một số hữu hạn.

Bài 8 trang 94 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\left\{\begin{array}{cc}\frac{x^2-9}{\left|x+3\right|}& \text{ khi }x\ne -3\\ a& \text{ khi }x=-3.\end{array}\right.$

a) Tìm $\underset{x\to -3^{+}}{\lim }f\left(x\right)-\underset{x\to -3^{-}}{\lim }f\left(x\right).$

b) Với giá trị nào của a thì hàm số liên tục tại x = ‒3?

Lời giải:

a) Khi $x>-3,f\left(x\right)=\frac{x^2-9}{\left|x+3\right|}=\frac{x^2-9}{x+3}=x-3$.

Khi $x<-3,f\left(x\right)=\frac{x^2-9}{\left|x+3\right|}=\frac{x^2-9}{-\left(x+3\right)}=3-x$.

Từ đó, $\underset{x\to -3^{+}}{\lim }f\left(x\right)=\underset{x\to -3^{+}}{\lim }\left(x-3\right)=-6$ và $\underset{x\to -3^{-}}{\lim }f\left(x\right)=\underset{x\to -3^{-}}{\lim }\left(3-x\right)=6$.

Suy ra $\underset{x\to -3^{+}}{\lim }f\left(x\right)-\underset{x\to -3^{-}}{\lim }f\left(x\right)=-6-6=-12.$

b) Do $\underset{x\to -3^{+}}{\lim }f\left(x\right)\ne \underset{x\to -3^{-}}{\lim }f\left(x\right),$ nên không tồn tại $\underset{x\to 3}{\lim }f\left(x\right)$.

Do đó, hàm số không liên tục tại x = ‒3 với mọi giá trị của a.

Bài 9 trang 95 SBT Toán 11 Tập 1: Cho hàm số $f\left(x\right)=\frac{2x+1}{x-3}$.

a) Xét tính liên tục của hàm số đã cho.

b) Tìm các giới hạn $\underset{x\to +\infty }{\lim }f\left(x\right);\underset{x\to -\infty }{\lim }f\left(x\right);\underset{x\to 3^{+}}{\lim }f\left(x\right);\underset{x\to 3}{\lim }f\left(x\right).$

Lời giải:

a) Ta có: x ‒ 3 ≠ 0 ⇔ x ≠ 3

f(x) là hàm phân thức có tập xác định D = ℝ ∖ {3} nên nó liên tục trên các khoảng (‒∞; 3) và (3; +∞).

b) Ta có:

⦁$\underset{x\to +\infty }{\lim }f\left(x\right)=\underset{x\to +\infty }{\lim }\frac{2x+1}{x-3}=\underset{x\to +\infty }{\lim }\frac{2+\frac{1}{x}}{1-\frac{3}{x}}=\frac{2}{1}=2.$

⦁$\underset{x\to -\infty }{\lim }f\left(x\right)=\underset{x\to -\infty }{\lim }\frac{2x+1}{x-3}=\underset{x\to -\infty }{\lim }\frac{2+\frac{1}{x}}{1-\frac{3}{x}}=\frac{2}{1}=2.$

⦁$\underset{x\to 3^{+}}{\lim }f\left(x\right)=\underset{x\to 3^{+}}{\lim }\frac{2x+1}{x-3}$

Vì $\underset{x\to 3^{+}}{\lim }\left(2x+1\right)=2\cdot 3+1=7;\underset{x\to 3^{+}}{\lim }\frac{1}{x-3}=+\infty$

Nên $\underset{x\to 3^{+}}{\lim }f\left(x\right)=\underset{x\to 3^{+}}{\lim }\frac{2x+1}{x-3}=+\infty .$

⦁ $\underset{x\to 3^{-}}{\lim }f\left(x\right)=\underset{x\to 3^{-}}{\lim }\frac{2x+1}{x-3}$

Vì $\underset{x\to 3^{-}}{\lim }\left(2x+1\right)=2\cdot 3+1=7;\underset{x\to 3-}{\lim }\frac{1}{x-3}=-\infty$

Nên $\underset{x\to 3^{-}}{\lim }f\left(x\right)=\underset{x\to 3^{-}}{\lim }\frac{2x+1}{x-3}=-\infty .$

Bài 10 trang 95 SBT Toán 11 Tập 1: Cho điểm M thay đổi trên parabol y = x²; H là hình chiếu vuông góc của M trên trục hoành. Gọi x là hoành độ của điểm H.

Tìm $\underset{x\to +\infty }{\lim }\left(\mathrm{OM}-\mathrm{MH}\right).$

Lời giải:

Ta có $M\left(x;x^2\right);\mathrm{OM}=\sqrt{x^2+x^4};\mathrm{MH}=\left|x^2\right|=x^2$.

Khi đó $\underset{x\to +\infty }{\text{lim}}\left(\mathrm{OM}-\mathrm{MH}\right)=\underset{x\to +\infty }{\text{lim}}\left(\sqrt{x^2+x^4}-x^2\right)$

$=\underset{x\to +\infty }{\text{lim}}\frac{\left(\sqrt{x^2+x^4}-x^2\right)\left(\sqrt{x^2+x^4}+x^2\right)}{\sqrt{x^2+x^4}+x^2}=\underset{x\to +\infty }{\text{lim}}\frac{x^2}{\sqrt{x^2+x^4}+x^2}$

$=\underset{x\to +\infty }{\text{lim}}\frac{1}{\sqrt{\frac{1}{x^2}+1}+1}=\frac{1}{2}.$

Bài 11 trang 95 SBT Toán 11 Tập 1: Chứng minh rằng phương trình x⁵ + 3x² ‒ 1 = 0 trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1) đều có ít nhất một nghiệm.

Lời giải:

Xét hàm số f(x) = x⁵ + 3x² ‒ 1. Hàm số này liên tục trên ℝ.

Ta có:

f(‒2) = (‒2)⁵ + 3.(‒2)² ‒ 1 = ‒32 + 12 ‒ 1 = ‒21.

f(‒1) = (‒1)⁵ + 3.(‒1)² ‒ 1 = ‒1 + 3 ‒ 1 = 1.

f(0) = 0⁵ + 3.0² ‒ 1 = ‒1.

f(1) = 1⁵ + 3.1² ‒ 1 = 3.

Do f(‒2).f(‒1) = ‒21 < 0 nên phương trình f(x) có nghiệm thuộc (‒2; ‒1).

Do f(‒1).f(0) < 0 nên phương trình f(x) = 0 có nghiệm thuộc (‒1; 0).

Do f(0).f(1) = ‒3 < 0 nên phương trình f(x) = 0có nghiệm thuộc (0; 1).

Vậy trong mỗi khoảng (‒2; ‒1), (‒1; 0) và (0; 1)phương trình f(x) = 0 hay x⁵ + 3x² ‒ 1 = 0 đều có ít nhất một nghiệm.

Bài 12 trang 95 SBT Toán 11 Tập 1: Tại một bể bơi có dạng hình tròn có đường kính AB = 10m, một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc $\alpha \left(0<\alpha <\frac{\pi }{2}\right),$ rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi S(α) là quãng đường người đó đã di chuyển.

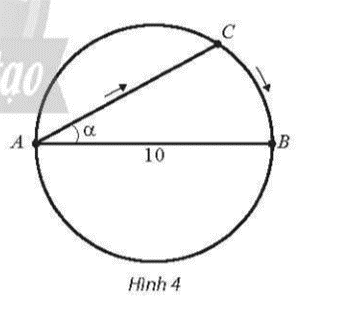
a) Viết công thức tính S(α) theo $\alpha \left(0<\alpha <\frac{\pi }{2}\right)$.

b) Xét tính liên tục của hàm số y = S(α) trên khoảng $\left(0;\frac{\pi }{2}\right)$.

c) Tính các giới hạn $\underset{x\to 0^{+}}{\lim }S\left(\alpha \right)$ và $\underset{x\to {\frac{\pi }{2}}^{+}}{\lim }S\left(\alpha \right).$

Lời giải:

Kí hiệu O là tâm hình tròn.

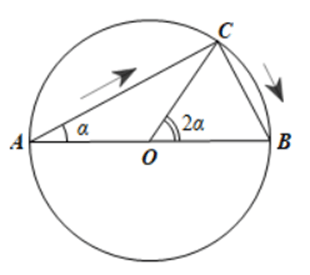
a) Do tam giác ABC vuông tại C nên AC = ABcosα = 10cosα (m).

Ta có $\widehat{\mathrm{BOC}}=2\widehat{\mathrm{BAC}}=2\alpha$.

Suy ra độ dài cung CB là $l=\mathrm{OB}.\widehat{\mathrm{BOC}}=5.2\alpha =10\alpha \left(\text{m}\right)$.

Quãng đường di chuyển (tính theo m) của người đó là:

$S\left(\alpha \right)=\mathrm{AC}+l=10\text{cos}\alpha +10\alpha =10\left(\alpha +\text{cos}\alpha \right)\left(0<\alpha <\frac{\pi }{2}\right)$

b) Do các hàm số y = α và y = cosα liên tục trên ℝ nên hàm số y = S(α) liên tục trên ℝ

Mà $\left(0;\frac{\pi }{2}\right)\subset ℝ$ nên hàm số y = S(α) liên tục trên $\left(0;\frac{\pi }{2}\right).$

c) Ta có:

$\underset{\alpha \to 0^{+}}{\lim }S\left(\alpha \right)=\underset{\alpha \to 0^{+}}{\lim }10\left(\alpha +\text{cos}\alpha \right)=10\cdot \left(0+\text{cos}0\right)=10\cdot \left(0+1\right)=10;$

$\underset{\alpha \to \frac{{\pi }^{+}}{2}}{\text{lim}}S\left(\alpha \right)=\underset{\alpha \to \frac{{\pi }^{+}}{2}}{\text{lim}}10\left(\alpha +\text{cos}\alpha \right)$$=10\cdot \left(\frac{\pi }{2}+\text{cos}\frac{\pi }{2}\right)=10\cdot \left(\frac{\pi }{2}+0\right)=5\pi .$

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục