Tại một bể bơi có dạng hình tròn có đường kính AB = 10m, một người xuất phát từ A bơi thẳng

Bài 12 trang 95 SBT Toán 11 Tập 1: Tại một bể bơi có dạng hình tròn có đường kính AB = 10m, một người xuất phát từ A bơi thẳng theo dây cung AC tạo với đường kính AB một góc $\alpha \left(0<\alpha <\frac{\pi }{2}\right),$ rồi chạy bộ theo cung nhỏ CB đến điểm B (Hình 4). Gọi S(α) là quãng đường người đó đã di chuyển.

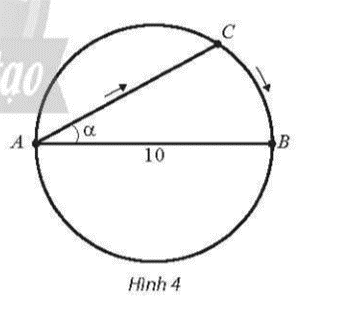
a) Viết công thức tính S(α) theo $\alpha \left(0<\alpha <\frac{\pi }{2}\right)$.

b) Xét tính liên tục của hàm số y = S(α) trên khoảng $\left(0;\frac{\pi }{2}\right)$.

c) Tính các giới hạn $\underset{x\to 0^{+}}{\lim }S\left(\alpha \right)$ và $\underset{x\to {\frac{\pi }{2}}^{+}}{\lim }S\left(\alpha \right).$

Trả lời

Kí hiệu O là tâm hình tròn.

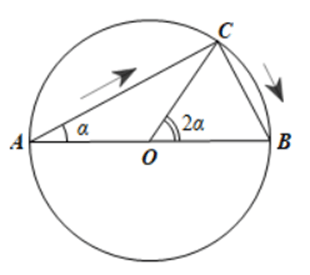
a) Do tam giác ABC vuông tại C nên AC = ABcosα = 10cosα (m).

Ta có $\widehat{\mathrm{BOC}}=2\widehat{\mathrm{BAC}}=2\alpha$.

Suy ra độ dài cung CB là $l=\mathrm{OB}.\widehat{\mathrm{BOC}}=5.2\alpha =10\alpha \left(\text{m}\right)$.

Quãng đường di chuyển (tính theo m) của người đó là:

$S\left(\alpha \right)=\mathrm{AC}+l=10\text{cos}\alpha +10\alpha =10\left(\alpha +\text{cos}\alpha \right)\left(0<\alpha <\frac{\pi }{2}\right)$

b) Do các hàm số y = α và y = cosα liên tục trên ℝ nên hàm số y = S(α) liên tục trên ℝ

Mà $\left(0;\frac{\pi }{2}\right)\subset ℝ$ nên hàm số y = S(α) liên tục trên $\left(0;\frac{\pi }{2}\right).$

c) Ta có:

$\underset{\alpha \to 0^{+}}{\lim }S\left(\alpha \right)=\underset{\alpha \to 0^{+}}{\lim }10\left(\alpha +\text{cos}\alpha \right)=10\cdot \left(0+\text{cos}0\right)=10\cdot \left(0+1\right)=10;$

$\underset{\alpha \to \frac{{\pi }^{+}}{2}}{\text{lim}}S\left(\alpha \right)=\underset{\alpha \to \frac{{\pi }^{+}}{2}}{\text{lim}}10\left(\alpha +\text{cos}\alpha \right)$$=10\cdot \left(\frac{\pi }{2}+\text{cos}\frac{\pi }{2}\right)=10\cdot \left(\frac{\pi }{2}+0\right)=5\pi .$

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài 2: Giới hạn của hàm số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3