Giải SBT Toán 11 (Chân trời sáng tạo) Bài 2: Giới hạn của hàm số

Sách bài tập Toán 11 Bài 2: Giới hạn của hàm số

Bài 1 trang 84 SBT Toán 11 Tập 1: Sử dụng định nghĩa, tìm các giới hạn sau:

a) $\underset{x\to -1}{\lim }\left(x^3-3x\right);$

b) $\underset{x\to 2}{\lim }\sqrt{2x+5};$

c) $\underset{x\to +\infty }{\lim }\frac{4-x}{2x+1}.$

Lời giải:

a) Giả sử (x_n) là dãy số bất kì thỏa mãn limx_n = ‒1.

Ta có: $\lim \left(x_n^3-3x_n\right)={\left({\text{limx}}_n\right)}^3-3\lim x_n$$={\left(-1\right)}^3-3\cdot \left(-1\right)=2.$

Vậy $\underset{x\to -1}{\lim }\left(x^3-3x\right)=2.$

b) Giả sử (x_n) là dãy số bất kì thỏa mãn $x\ge -\frac{5}{2}$ với mọi n và limx_n = 2.

Ta có:

$\lim \sqrt{2x_n+5}=\sqrt{\lim 2x_n+\lim 5}=\sqrt{2\lim x_n+\lim 5}$

$=\sqrt{2\cdot 2+5}=\sqrt{9}=3.$

Vậy $\underset{x\to 2}{\lim }\sqrt{2x+5}=3.$

c) Giả sử (x_n) là dãy số bất kì thỏa mãn limx_n = +∞.

Ta có: $\lim \frac{4-x_n}{2x_n+1}=\frac{\lim \frac{4}{x_n}-\lim 1}{\lim 2x_n+\lim \frac{1}{x_n}}=\frac{0-1}{2+0}=-\frac{1}{2}.$

Vậy $\underset{x\to +\infty }{\lim }\frac{4-x}{2x+1}=-\frac{1}{2}.$

Bài 2 trang 84 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\underset{x\to -3}{\lim }\left(8+3x-x^2\right);$

b) $\underset{x\to 2}{\lim }\left[\left(5x-1\right)\left(2-4x\right)\right];$

c) $\underset{x\to -2}{\lim }\frac{x^2-x}{{\left(2x+1\right)}^2};$

d) $\underset{x\to -1}{\lim }\sqrt{10-2x^2}.$

Lời giải:

a)$\underset{x\to -3}{\lim }\left(8+3x-x^2\right)=1+3\underset{x\to -3}{\lim }x-\underset{x\to -3}{\lim }{x}^2$

$=8+3\cdot \left(-3\right)-{\left(-3\right)}^2=-10.$

b) $\underset{x\to 2}{\lim }\left[\left(5x-1\right)\left(2-4x\right)\right]=\underset{x\to 2}{\lim }\left(5x-1\right)\cdot \underset{x\to 2}{\lim }\left(2-4x\right)$

$=\left(5\underset{x\to 2}{\lim }x-1\right)\cdot \left(2-4\underset{x\to 2}{\lim }x\right)$

= (5.2 ‒ 1)(2 ‒ 4.2) = ‒54.

c) $\underset{x\to -2}{\lim }\frac{x^2-x}{{\left(2x+1\right)}^2}=\frac{\underset{x\to -2}{\lim }\left(x^2-x\right)}{\underset{x\to -2}{\lim }\left(4x^2+4x+1\right)}$$=\frac{\underset{x\to -2}{\lim }{x}^2-\underset{x\to -2}{\lim }x}{4\underset{x\to -2}{\lim }{x}^2+4\underset{x\to -2}{\lim }x+1}$

$=\frac{{\left(-2\right)}^2-\left(-2\right)}{4\cdot {\left(-2\right)}^2+4\cdot \left(-2\right)+1}=\frac{6}{9}=\frac{2}{3}.$

d) $\underset{x\to -1}{\lim }\sqrt{10-2x^2}=\sqrt{\underset{x\to -1}{\lim }\left(10-2x^2\right)}=\sqrt{10-\underset{x\to -1}{\lim }2x^2}$

$=\sqrt{10-2\underset{x\to -1}{\lim }{x}^2}=\sqrt{10-2.{\left(-1\right)}^2}=\sqrt{8}=2\sqrt{2}.$

Bài 3 trang 84 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\underset{x\to -2}{\lim }\frac{x^2-4}{x+2};$

b) $\underset{x\to 1}{\lim }\frac{x^3-1}{1-x};$

c) $\underset{x\to 3}{\lim }\frac{x^2-4x+3}{x-3};$

d) $\underset{x\to -2}{\lim }\frac{2-\sqrt{x+6}}{x+2};$

e) $\underset{x\to 0}{\lim }\frac{x}{\sqrt{x+1}-1};$

g) $\underset{x\to 2}{\lim }\frac{x^2-4x+4}{x^2-4}.$

Lời giải:

a) $\underset{x\to -2}{\lim }\frac{x^2-4}{x+2}=\underset{x\to -2}{\lim }\frac{\left(x+2\right)\left(x-2\right)}{x+2}$$=\underset{x\to -2}{\lim }\left(x-2\right)=-2-2=-4.$

b) $\underset{x\to 1}{\lim }\frac{x^3-1}{1-x}=\underset{x\to 1}{\lim }\frac{\left(x-1\right)\left(x^2+x+1\right)}{-\left(x-1\right)}$

$=\underset{x\to 1}{\lim }\left[-\left(x^2+x+1\right)\right]=-\left(\underset{x\to 1}{\lim }{x}^2+\underset{x\to 1}{\lim }x+1\right)=-3.$

c) $\underset{x\to 3}{\lim }\frac{x^2-4x+3}{x-3}=\underset{x\to 3}{\lim }\frac{\left(x-1\right)\left(x-3\right)}{x-3}$$=\underset{x\to 3}{\lim }\left(x-1\right)=3-1=2$

d) $\underset{x\to -2}{\text{lim}}\frac{2-\sqrt{x+6}}{x+2}=\underset{x\to -2}{\text{lim}}\frac{\left(2-\sqrt{x+6}\right)\left(2+\sqrt{x+6}\right)}{\left(x+2\right)\left(2+\sqrt{x+6}\right)}$

$=\underset{x\to -2}{\text{lim}}\frac{4-\left(x+6\right)}{\left(x+2\right)\left(2+\sqrt{x+6}\right)}=\underset{x\to -2}{\text{lim}}\frac{-\left(x+2\right)}{\left(x+2\right)\left(2+\sqrt{x+6}\right)}$

$=\underset{x\to -2}{\text{lim}}\frac{-1}{2+\sqrt{x+6}}=\frac{-1}{2+\sqrt{-2+6}}=-\frac{1}{4}.$

e) $\underset{x\to 0}{\text{lim}}\frac{x}{\sqrt{x+1}-1}=\underset{x\to 0}{\text{lim}}\frac{x\left(\sqrt{x+1}+1\right)}{\left(\sqrt{x+1}-1\right)\left(\sqrt{x+1}+1\right)}$

$=\underset{x\to 0}{\text{lim}}\frac{x\left(\sqrt{x+1}+1\right)}{\left(x+1\right)-1}=\underset{x\to 0}{\text{lim}}\left(\sqrt{x+1}+1\right)=2.$

g) $\underset{x\to 2}{\lim }\frac{x^2-4x+4}{x^2-4}=\underset{x\to 2}{\lim }\frac{{\left(x-2\right)}^2}{\left(x+2\right)\left(x-2\right)}$

$=\underset{x\to 2}{\lim }\frac{x-2}{x+2}=\frac{\underset{x\to 2}{\lim }\left(x-2\right)}{\underset{x\to 2}{\lim }\left(x+2\right)}=\frac{0}{4}=0.$

Bài 4 trang 84 SBT Toán 11 Tập 1: Cho hai hàm số f(x) và g(x) có $\underset{x\to 4}{\lim }f\left(x\right)=2$ và $\underset{x\to 4}{\lim }g\left(x\right)=-3.$ Tìm các giới hạn:

a) $\underset{x\to 4}{\lim }\left[g\left(x\right)-3f\left(x\right)\right];$

b) $\underset{x\to 4}{\lim }\frac{2f\left(x\right)\cdot g\left(x\right)}{{\left[f\left(x\right)+g\left(x\right)\right]}^2}.$

Lời giải:

a) $\underset{x\to 4}{\lim }\left[g\left(x\right)-3f\left(x\right)\right]=\left(-3\right)-3\cdot 2=-9.$

b) $\underset{x\to 4}{\lim }\frac{2f\left(x\right)\cdot g\left(x\right)}{{\left[f\left(x\right)+g\left(x\right)\right]}^2}=\frac{2\cdot 2\cdot \left(-3\right)}{{\left[2+\left(-3\right)\right]}^2}=\frac{-12}{1}=-12.$

Bài 5 trang 84 SBT Toán 11 Tập 1: Cho hai hàm số f(x) và g(x) có $\underset{x\to +\infty }{\lim }f\left(x\right)=3$ và $\underset{\mathrm{x}\to +\mathrm{\infty }}{\lim }\left[\mathrm{f}\left(\mathrm{x}\right)+2\mathrm{g}\left(\mathrm{x}\right)\right]=7.$

Tìm $\underset{x\to +\infty }{\lim }\frac{2f\left(x\right)+g\left(x\right)}{2f\left(x\right)-g\left(x\right)}.$

Lời giải:

Ta có $\underset{\mathrm{x}\to +\mathrm{\infty }}{\lim }\left[\mathrm{f}\left(\mathrm{x}\right)+2\mathrm{g}\left(\mathrm{x}\right)\right]=7.$

$\Rightarrow \underset{x\to +\infty }{\lim }f\left(x\right)+2\underset{x\to +\infty }{\lim }g\left(x\right)=7$

$\Rightarrow 3+2\underset{x\to +\infty }{\lim }g\left(x\right)=7$

$\Rightarrow \underset{x\to +\infty }{\lim }g\left(x\right)=2$

Suy ra $\underset{x\to +\infty }{\lim }\frac{2f\left(x\right)+g\left(x\right)}{2f\left(x\right)-g\left(x\right)}=\frac{2\underset{x\to +\infty }{\lim }f\left(x\right)+\underset{x\to +\infty }{\lim }g\left(x\right)}{2\underset{x\to +\infty }{\lim }f\left(x\right)-\underset{x\to +\infty }{\lim }g\left(x\right)}$$=\frac{2\cdot 3+2}{2\cdot 3-2}=2.$

Bài 6 trang 84 SBT Toán 11 Tập 1: Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}3\mathrm{x}+4,\mathrm{x}\le -1\\ 3-2{\mathrm{x}}^2,\mathrm{x}>-1\end{array}\right..$

Tìm các giới hạn $\underset{x\to -1^{+}}{\lim }f\left(x\right),\underset{x\to -1^{-}}{\lim }f\left(x\right)$ và $\underset{x\to -1}{\lim }f\left(x\right).$

Lời giải:

Ta có:

⦁ $\underset{x\to -1^{+}}{\lim }f\left(x\right)=\underset{x\to -1^{+}}{\lim }\left(3-2x^2\right)=\underset{x\to -1^{+}}{\lim }3-2\underset{x\to -1^{+}}{\lim }{x}^2$

$=3-2\cdot {\left(-1\right)}^2=1.$

⦁$\underset{x\to -1^{-}}{\lim }f\left(x\right)=\underset{x\to -1^{-}}{\lim }\left(3x+4\right)=3\underset{x\to -1^{-}}{\lim }x+4=3\cdot \left(-1\right)+4=1.$

⦁ Vì $\underset{x\to -1^{+}}{\lim }f\left(x\right)=\underset{x\to -1^{-}}{\lim }f\left(x\right)=1$ nên $\underset{x\to -1}{\lim }f\left(x\right)=1.$

Bài 7 trang 84 SBT Toán 11 Tập 1: Cho hàm số $\mathrm{f}\left(\mathrm{x}\right)=\left\{\begin{array}{l}2\mathrm{x}+1,\mathrm{x}\le 1\\ \sqrt{{\mathrm{x}}^2+\mathrm{a}},\mathrm{x}>1.\end{array}\right.$

Tìm giá trị của tham số a sao cho tồn tại giới hạn $\underset{x\to 1}{\lim }f\left(x\right).$

Lời giải:

Ta có: $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{-}}{\lim }\left(2x+1\right)=2\underset{x\to 1^{-}}{\lim }x+1=2\cdot 1+1=3;$

$\underset{x\to 1^{+}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }\sqrt{x^2+a}=\sqrt{\underset{x\to 1^{+}}{\lim }\left(x^2+a\right)}=\sqrt{1+a};$

Để tồn tại $\underset{x\to 1}{\lim }f\left(x\right)$ thì $\underset{x\to 1^{-}}{\lim }f\left(x\right)=\underset{x\to 1^{+}}{\lim }f\left(x\right)$

Tức là $\sqrt{1+a}=3,$ suy ra a = 8.

Bài 8 trang 85 SBT Toán 11 Tập 1: Mỗi giới hạn sau có tồn tại không? Nếu có, hãy tìm giới hạn đó.

a) $\underset{\mathrm{x}\to 0}{\lim }\frac{{\mathrm{x}}^2}{\left|\mathrm{x}\right|};$

b) $\underset{\mathrm{x}\to 2}{\lim }\frac{{\mathrm{x}}^2-2\mathrm{x}}{\left|\mathrm{x}-2\right|}.$

Lời giải:

a) Ta có:

⦁$\underset{x\to 0^{-}}{\lim }\frac{x^2}{\left|x\right|}=\underset{x\to 0^{-}}{\lim }\frac{x^2}{-x}=\underset{x\to 0^{-}}{\lim }\frac{x}{-1}=\underset{x\to 0^{-}}{\lim }\left(-x\right)=0;$

⦁$\underset{x\to 0^{+}}{\lim }\frac{x^2}{\left|x\right|}=\underset{x\to 0^{+}}{\lim }\frac{x^2}{x}=\underset{x\to 0^{+}}{\lim }\frac{x}{1}=\underset{x\to 0^{+}}{\lim }x=0.$

Do $\underset{x\to 0^{-}}{\lim }\frac{x^2}{\left|x\right|}=\underset{x\to 0^{+}}{\lim }\frac{x^2}{\left|x\right|}=0$ nên tồn tại giới hạn $\underset{x\to 0}{\lim }\frac{x^2}{\left|x\right|}$ và $\underset{x\to 0}{\lim }\frac{x^2}{\left|x\right|}=0.$

b) Ta có:

⦁$\underset{x\to 2^{+}}{\lim }\frac{x^2-2x}{\left|x-2\right|}=\underset{x\to 2^{+}}{\lim }\frac{x^2-2x}{x-2}$$=\underset{x\to 2^{+}}{\lim }\frac{x\left(x-2\right)}{x-2}\text{=}\underset{x\to 2^{+}}{\lim }x=2.$

⦁ $\underset{x\to 2^{-}}{\lim }\frac{x^2-2x}{\left|x-2\right|}=\underset{x\to 2^{-}}{\lim }\frac{x^2-2x}{2-x}$$=\underset{x\to 2^{-}}{\lim }\frac{x\left(x-2\right)}{2-x}\underset{x\to 2^{-}}{\lim }\left(-x\right)=-2.$

Do $\underset{x\to 2^{+}}{\lim }\frac{x^2-2x}{\left|x-2\right|}\ne \underset{x\to 2-}{\lim }\frac{x^2-2x}{\left|x-2\right|}$ nên không tồn tại giới hạn $\underset{x\to 2}{\lim }\frac{x^2-2x}{\left|x-2\right|}.$

Bài 9 trang 85 SBT Toán 11 Tập 1: Tìm các giới hạn sau:

a) $\underset{x\to +\infty }{\lim }\frac{x}{x+4};$

b) $\underset{x\to -\infty }{\lim }\frac{2x^2+1}{{\left(2x+1\right)}^2};$

c) $\underset{x\to -\infty }{\lim }\frac{3x+1}{\sqrt{x^2-2x}};$

d) $\underset{x\to +\infty }{\lim }\left(x-\sqrt{x^2+2x}\right).$

Lời giải:

a) $\underset{x\to +\infty }{\lim }\frac{x}{x+4}=\underset{x\to +\infty }{\lim }\frac{1}{1+\frac{4}{x}}=\frac{1}{1+4\cdot 0}=1.$

b) $\underset{x\to -\infty }{\lim }\frac{2x^2+1}{{\left(2x+1\right)}^2}=\underset{x\to -\infty }{\lim }\frac{2+\frac{1}{x^2}}{{\left(2+\frac{1}{x}\right)}^2}=\frac{2+0}{{\left(2+0\right)}^2}=\frac{1}{2}.$

c) Với x < 0 thì $\sqrt{x^2}=\mathrm{|x|}=-x,$ nên ta có:

$\underset{x\to -\infty }{\lim }\frac{3x+1}{\sqrt{x^2-2x}}=\underset{x\to -\infty }{\lim }\frac{x\left(3+\frac{1}{x}\right)}{-x\sqrt{1-\frac{2}{x}}}$$=\underset{x\to -\infty }{\lim }\frac{3+\frac{1}{x}}{-\sqrt{1-\frac{2}{x}}}=-\frac{3+0}{\sqrt{1-2\cdot 0}}=-3.$

d) $\underset{x\to +\infty }{\lim }\left(x-\sqrt{x^2+2x}\right)=\underset{x\to +\infty }{\lim }\frac{\left(x-\sqrt{x^2+2x}\right)\left(x+\sqrt{x^2+2x}\right)}{x+\sqrt{x^2+2x}}$

$=\underset{x\to +\infty }{\lim }\frac{x^2-\left(x^2+2x\right)}{x+\sqrt{x^2+2x}}=\underset{x\to +\infty }{\lim }\frac{-2x}{x+x\sqrt{1+\frac{2}{x}}}$

$=\underset{x\to +\infty }{\lim }\frac{-2}{1+\sqrt{1+\frac{2}{x}}}=\frac{-2}{1+1}=-1.$

Bài 10 trang 85 SBT Toán 11 Tập 1: Tính các giới hạn sau:

a) $\underset{x\to -\infty }{\lim }\left(x^3+2x^2-1\right);$

b) $\underset{x\to +\infty }{\lim }\frac{x^3+2x^2}{3x^2+1};$

c) $\underset{x\to -\infty }{\lim }\sqrt{x^2-2x+3}.$

Lời giải:

a) $\underset{x\to -\infty }{\lim }\left(x^3+2x^2-1\right)=\underset{x\to -\infty }{\lim }\left[x^3\left(1+\frac{2}{x}-\frac{1}{x^3}\right)\right]$

Ta có $\underset{x\to -\infty }{\lim }{x}^3=-\infty$ và $\underset{x\to -\infty }{\lim }\left(1+\frac{2}{x}-\frac{1}{x^3}\right)=1+0-0=1.$

Suy ra $\underset{x\to -\infty }{\lim }\left(x^3+2x^2-1\right)=\underset{x\to -\infty }{\lim }\left[x^3\left(1+\frac{2}{x}-\frac{1}{x^3}\right)\right]=-\infty .$

b) $\underset{x\to +\infty }{\lim }\frac{x^3+2x^2}{3x^2+1}=\underset{x\to +\infty }{\lim }\left[x\cdot \frac{x^2+2x}{3x^2+1}\right]$

Ta có $\underset{x\to +\infty }{\lim }x=+\infty$ và $\underset{x\to +\infty }{\lim }\frac{x^2+2x}{3x^2+1}=\underset{x\to +\infty }{\lim }\frac{1+\frac{2}{x}}{3+\frac{1}{x^2}}=\frac{1}{3}$

Suy ra $\underset{x\to +\infty }{\lim }\frac{x^3+2x^2}{3x^2+1}=\underset{x\to +\infty }{\lim }\left[x\cdot \frac{x^2+2x}{3x^2+1}\right]=+\infty .$

c) $\underset{x\to -\infty }{\lim }\sqrt{x^2-2x+3}=\underset{x\to -\infty }{\lim }\sqrt{x^2\left(1-\frac{2}{x}+\frac{3}{x^2}\right)}$

$=\underset{x\to -\infty }{\lim }\left(\left|x\right|\sqrt{1-\frac{2}{x}+\frac{3}{x^2}}\right)$

Ta có $\underset{x\to -\infty }{\lim }\left|x\right|=\underset{x\to -\infty }{\lim }\left(-x\right)=+\infty$ và $\underset{x\to -\infty }{\lim }\sqrt{1-\frac{2}{x}+\frac{3}{x^2}}=1$

Suy ra $\underset{x\to -\infty }{\lim }\sqrt{x^2-2x+3}=\underset{x\to -\infty }{\lim }\left(\left|x\right|\sqrt{1-\frac{2}{x}+\frac{3}{x^2}}\right)=+\infty .$

Bài 11 trang 85 SBT Toán 11 Tập 1: Tìm giá trị của các tham số a và b, biết rằng:

a) $\underset{x\to 2}{\lim }\frac{\mathrm{ax}+b}{x-2}=5;$

b) $\underset{x\to 1}{\lim }\frac{a\sqrt{x}+b}{x-1}=3.$

Lời giải:

a) Do $\underset{x\to 2}{\lim }\left(x-2\right)=2-2=0$ nên để tồn tại giới hạn hữu hạn $\underset{x\to 2}{\lim }\frac{\mathrm{ax}+b}{x-2}=5,$ trước hết ta phải có $\underset{x\to 2}{\lim }\left(\mathrm{ax}+b\right)=0$ hay 2a + b = 0, suy ra b = ‒2a.

Khi đó,$\underset{x\to 2}{\lim }\frac{\mathrm{ax}+b}{x-2}=\underset{x\to 2}{\lim }\frac{\mathrm{ax}-2a}{x-2}$$=\underset{x\to 2}{\lim }\frac{a\left(x-2\right)}{x-2}=\underset{x\to 2}{\lim }a=a$

Suy ra a = 5 và b = ‒10.

b) Do $\underset{x\to 1}{\lim }\left(x-1\right)=1-1=0$ nên để tồn tại giới hạn hữu hạn $\underset{x\to 1}{\lim }\frac{a\sqrt{x}+b}{x-1}=3,$ trước hết ta phải có $\underset{x\to 1}{\lim }\left(a\sqrt{x}+b\right)=0$ hay a + b = 0, suy ra b = ‒a.

Khi đó, $\underset{x\to 1}{\lim }\frac{a\sqrt{x}+b}{x-1}=\underset{x\to 1}{\lim }\frac{a\sqrt{x}-a}{x-1}$ $=\underset{x\to 1}{\lim }\frac{a\left(\sqrt{x}-1\right)}{x-1}=\underset{x\to 1}{\lim }\frac{a\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}$

$=\underset{x\to 1}{\text{lim}}\frac{a\left(x-1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}=\underset{x\to 1}{\text{lim}}\frac{a}{\sqrt{x}+1}=\frac{a}{2}.$

Suy ra $\frac{a}{2}=3$ hay a = 6, suy ra b = ‒6.

Bài 12 trang 85 SBT Toán 11 Tập 1: Trong mặt phẳng toạ độ Oxy, cho điểm M(t, t²), t > 0, nằm trên đường parabol y = x². Đường trung trực của đoạn thẳng OM cắt trục tung tại N. Điểm N dần đến điểm nào khi điểm M dần đến điểm O?

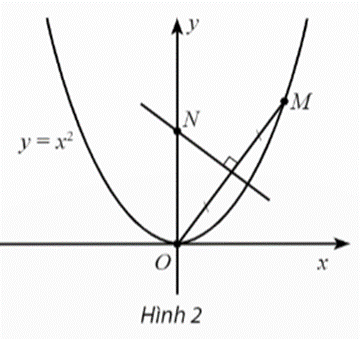
Lời giải:

Trung điểm của đoạn thẳng OM là $I\left(\frac{t}{2};\frac{t^2}{2}\right)$

Đường trung trực của OM nhận $\overrightarrow{\mathrm{OM}}=\left(t,t^2\right)$ làm vectơ pháp tuyến và đi qua điểm $I\left(\frac{t}{2};\frac{t^2}{2}\right)$ nên có phương trình $d:t\left(x-\frac{t}{2}\right)+t^2\left(y-\frac{t^2}{2}\right)=0$.

Thay x = 0 vào phương trình của d, ta nhận được $y=\frac{1}{2}\left(1+t^2\right)$.

Suy ra $N\left(0;\frac{1}{2}\left(1+t^2\right)\right)$

Điểm M dần đến điểm O khi t dần đến 0⁺. Ta có $\underset{x\to 0^{+}}{\lim }\frac{1}{2}\left(1+t^2\right)=\frac{1}{2}$.

Suy ra khi điểm dần đến điểm thì điểm dần đến điểm $A\left(0;\frac{1}{2}\right)$.

Xem thêm các bài giải SBT Toán lớp 11 Chân trời sáng tạo hay, chi tiết khác:

Bài tập cuối chương 2

Bài 1: Giới hạn của dãy số

Bài 3: Hàm số liên tục

Bài tập cuối chương 3