Giải SBT Toán 10 (Kết nối tri thức) Bài tập ôn tập cuối năm

Giải Sách bài tập Toán 10 Bài tập ôn tập cuối năm

Giải SBT Toán 10 trang 70 Tập 2

Bài 1 trang 70 SBT Toán 10 Tập 2: Cho các mệnh đề:

P: “Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt”;

Q: “Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”.

a) Hãy phát biểu các mệnh đề: P ⇒ Q, Q ⇒ P, P ⇔ Q, $\overline{P}\Rightarrow \overline{Q}$ . Xét tính đúng sai của các mệnh đề này.

b) Dùng các khái niệm “điều kiện cần” và “điều kiện đủ” để diễn tả mệnh đề P ⇒ Q.

c) Gọi X là tập hợp các phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt, Y là tập hợp các phương trình bậc hai ax² + bx + c = 0 có hệ số a và c trái dấu. Nêu mối quan hệ giữa hai tập hợp X và Y.

Lời giải:

a)

+ Mệnh đề P ⇒ Q: “Nếu phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt thì phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”. Đây là mệnh đề đúng.

+ Mệnh đề Q ⇒ P: “ Nếu phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0 thì phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt”. Đây là mệnh đề đúng.

+ Mệnh đề P ⇔ Q: “Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt khi và chỉ khi phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0”. Do P ⇒ Q, Q ⇒ P đều là các mệnh đề đúng nên mệnh đề P ⇔ Q là mệnh đề đúng.

+ Mệnh đề $\overline{P}\Rightarrow \overline{Q}$

Mệnh đề $\overline{P}$  là mệnh đề phủ định của mệnh đề P và được phát biểu là: “Phương trình bậc hai ax² + bx + c = 0 không có hai nghiệm phân biệt”.

Mệnh đề $\overline{Q}$  là mệnh đề phủ định của mệnh đề Q và được phát biểu là: “Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac ≤ 0”.

Khi đó, ta phát biểu mệnh đề $\overline{P}\Rightarrow \overline{Q}$ : “Nếu phương trình bậc hai ax² + bx + c = 0 không có hai nghiệm phân biệt thì phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac ≤ 0”. Mệnh đề này là mệnh đề đúng.

b)

+ Phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt là điều kiện đủ để phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0.

+ Phương trình bậc hai ax² + bx + c = 0 có biệt thức ∆ = b² – 4ac > 0 là điều kiện cần để phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt.

c) Ta có các phương trình bậc hai ax² + bx + c = 0 có hệ số a và c trái dấu thì luôn có hai nghiệm trái dấu, hiển nhiên đây là hai nghiệm phân biệt. Nhưng các phương trình bậc hai ax² + bx + c = 0 có hai nghiệm phân biệt thì hai nghiệm này chưa chắc đã trái dấu.

Do đó mọi phần tử của tập hợp Y thì đều là phần tử của tập hợp X.

Vậy Y là tập con của tập hợp X và ta viết Y ⊂ X.

Bài 2 trang 70 SBT Toán 10 Tập 2: a) Biểu diễn hình học tập nghiệm D của hệ bất phương trình bậc nhất hai ẩn sau:

$\left\{\begin{array}{c}x\ge 0\\ y\ge 0\\ 3x-2y\ge -6\\ 2x+y\le 10\end{array}\right.$.

b) Từ kết quả ở câu a), tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D, biết rằng giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D.

Lời giải:

a) Ta xác định miền nghiệm của từng bất phương trình trong hệ đã cho như sau:

Bước 1: Trục Oy có phương trình x = 0 và điểm (1; 0) thỏa mãn 1 > 0. Do đó miền nghiệm của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1; 0) (miền không bị gạch).

Bước 2: Trục Ox có phương trình y = 0 và điểm (0; 1) thỏa mãn 1 > 0. Do đó, miền nghiệm của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0; 1) (miền không bị gạch).

Bước 3: Vẽ đường thẳng d₁: 3x – 2y = – 6. Lấy điểm O(0; 0) không thuộc d₁ và thay x = 0, y = 0 vào biểu thức 3x – 2y ta được: 3 . 0 – 2 . 0 = 0 > – 6. Do đó, miền nghiệm của bất phương trình 3x – 2y ≥ – 6 là nửa mặt phẳng bờ d₁ chứa điểm O(0; 0) (miền không bị gạch).

Bước 4: Vẽ đường thẳng d₂: 2x + y = 10. Lấy điểm O(0; 0) không thuộc d₂ và thay x = 0, y = 0 vào biểu thức 2x + y ta được: 2 . 0 + 0 = 0 < 10. Do đó, miền nghiệm của bất phương trình 2x + y ≤ 10 là nửa mặt phẳng bờ d₂ chứa điểm O(0; 0) (miền không bị gạch).

Vậy miền nghiệm D của hệ bất phương trình đã cho là miền tứ giác OABC (miền không bị gạch), trong đó A(0; 3), B(2; 6), C(5; 0), như hình vẽ sau:

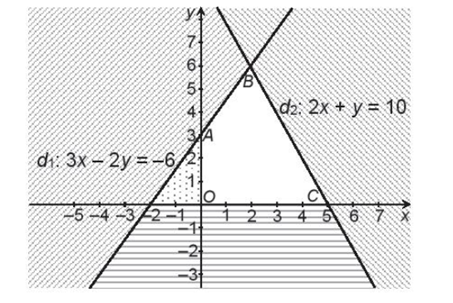
b) Vì giá trị lớn nhất (tương ứng, nhỏ nhất) của F đạt được tại một trong các đỉnh của miền đa giác D, do đó ta tính giá trị của F tại (x; y) là tọa độ các đỉnh O, A, B, C.

Ta có: F(0; 0) = 2 . 0 + 3 . 0 = 0;

F(0; 3) = 2 . 0 + 3 . 3 = 9;

F(2; 6) = 2 . 2 + 3 . 6 = 22;

F(5; 0) = 2 . 5 + 3 . 0 = 10.

Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức F(x; y) = 2x + 3y trên miền D lần lượt là 22 và 0.

Bài 3 trang 70 SBT Toán 10 Tập 2: Cho tam thức bậc hai f(x) = ax² + bx + c với đồ thị là parabol có đỉnh I(1; 4) và đi qua điểm A(2; 3).

a) Xác định các hệ số a, b, c của tam thức bậc hai f(x).

b) Vẽ parabol này.

c) Từ đồ thị đã vẽ ở câu b), hãy cho biết khoảng đồng biến, khoảng nghịch biến và tập giá trị của hàm số y = f(x).

d) Lập bảng xét dấu để giải bất phương trình $\frac{f\left(x\right)}{x-2}\ge 0$ .

Lời giải:

a) Parabol có đỉnh là I(1; 4) nên có phương trình dạng y = a(x – 1)² + 4.

Vì điểm A(2; 3) thuộc parabol nên ta có:

3 = a(2 – 1)² + 4 ⇔ a + 4 = 3 ⇔ a = – 1.

Vậy tam thức bậc hai cần tìm là f(x) = –(x – 1)² + 4 hay f(x) = – x² + 2x + 3.

Suy ra các hệ số là: a = – 1; b = 2; c = 3.

b) Ta có: a = – 1 < 0 nên parabol quay bề lõm xuống dưới.

Đỉnh parabol là I(1; 4).

Trục đối xứng x = 1.

Giao điểm của parabol với trục Oy là (0; 3). Điểm đối xứng với điểm (0; 3) qua trục đối xứng x = 1 là (2; 3).

Giao điểm của parabol với trục Ox là (– 1; 0) và (3; 0).

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ.

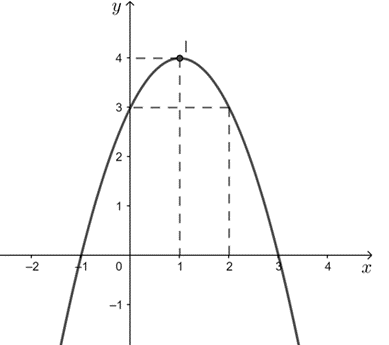
c) Từ đồ thị trên ta thấy:

- Hàm số đồng biến trên khoảng (– ∞; 1) và nghịch biến trên khoảng (1; + ∞).

- Tập giá trị của hàm số là (– ∞; 4].

d) Xét bất phương trình $\frac{f\left(x\right)}{x-2}\ge 0$ , hay $\frac{-x^2+2x+3}{x-2}\ge 0$ .

Tam thức f(x) = – x² + 2x + 3 có ∆' = 1² – (– 1) . 3 = 4 > 0 và a = – 1 < 0, f(x) có hai nghiệm phân biệt x₁ = – 1 và x₂ = 3. Do đó, f(x) > 0 với mọi x ∈ (– 1; 3) và f(x) < 0 với mọi x ∈ (– ∞; – 1) ∪ (3; + ∞).

Ta có bảng xét dấu sau:

 Vậy tập nghiệm của bất phương trình đã cho là S = (– ∞; – 1] ∪ (2; 3].

Giải SBT Toán 10 trang 71 Tập 2

Bài 4 trang 71 SBT Toán 10 Tập 2: Một quả bóng chày được đánh đi với vận tốc 35 m/s hợp với phương ngang một góc bằng 45° ở độ cao 1 m so với mặt sân phẳng ở chỗ vụt bóng. Bỏ qua sức cản của không khí và lấy g = 9,8 m/s².

a) Biết rằng quỹ đạo chuyển động của quả bóng chày được cho bởi phương trình:

$y=\frac{-g}{2v_0^2{\cos }^2\alpha }{x}^2+x\tan \alpha +h$,

trong đó x là quãng đường (tính bằng mét) quả bóng bay được theo phương ngang, h là độ cao của quả bóng lúc được đánh đi so với mặt đất, vận tốc ban đầu v₀ hợp với phương ngang một góc α.

Viết phương trình chuyển động của quả bóng chày.

b) Tính độ cao lớn nhất của quả bóng chày.

c) Tính tầm xa của quả bóng chày, tức là khoảng cách từ mặt đất ở chỗ đánh bóng và nơi quả bóng chạm đất (kết quả làm tròn đến hàng đơn vị).

d) Có một hàng rào cao 4 m cách chỗ đánh bóng 125 m theo hướng đánh bóng. Hỏi quả bóng chày được đánh đi như trên có bị bay qua hàng rào đó hay không?

Lời giải:

a) Ta có: g = 9,8 m/s², α = 45°, h = 1 m, v₀ = 35 m/s.

Do đó, phương trình chuyển động của quả bóng chày là:

$y=\frac{-\mathrm{9,8}}{{2.35}^2.{\cos }^{2}45°}{x}^2+x\tan 45°+1$.

Hay y = $\frac{-1}{125}{x}^2$  + x + 1.

b) Quả bóng chày đạt độ cao lớn nhất tức là hàm số y = $\frac{-1}{125}{x}^2$  + x + 1 đạt giá trị lớn nhất.

Hàm số y = $\frac{-1}{125}{x}^2$  + x + 1 là hàm số bậc hai nên đồ thị là một parabol.

Vì hệ số a = $\frac{-1}{125}<0$ , do đó hàm số đạt giá trị lớn nhất bằng tung độ đỉnh của parabol và giá trị lớn nhất này đạt được tại hoành độ đỉnh của parabol là x = $\frac{-b}{2a}=\frac{-1}{2.\frac{-1}{125}}=\mathrm{62,5}$ .

Khi đó, tung độ đỉnh y = $\frac{-1}{125}{\mathrm{.62,5}}^2+\mathrm{62,5}+1$  = 32,25.

Vậy độ cao cực đại của quả bóng chày là 32,25 m.

c) Bóng chạm đất khi y = 0.

Xét y = 0 ⇔ $\frac{-1}{125}{x}^2$  + x + 1 = 0 ⇔ x ≈ 126 hoặc x ≈ – 1 (loại).   

Vậy tầm xa của quả bóng chày là khoảng 126 m.

d) Quả bóng chày không bị bay qua hàng rào khi độ cao của quả bóng chày nhỏ hơn độ cao của hàng rào là 4 m.

Xét y < 4 ⇔ $\frac{-1}{125}{x}^2$  + x + 1 < 4 ⇔ x² – 125x + 375 > 0 ⇔ x < 3 hoặc x > 122.

Do 125 > 122.

Vậy quả bóng chày không bị bay qua hàng rào khi được đánh đi ở vị trí cách hàng rào 125 m.

Bài 5 trang 71 SBT Toán 10 Tập 2: Một công ty thời trang thấy rằng khi một loại áo phông được bán ở mức giá x (nghìn đồng) một chiếc thì số lượng áo phông bán được n cho bởi phương trình nhu cầu

n = 21 000 – 150x.

a) Tìm công thức biểu diễn doanh thu R như là hàm của giá bán x. Tìm miền xác định của hàm số R = R(x).

b) Giá bán nào sẽ làm cho doanh thu đạt cực đại? Tính doanh thu cực đại đó và số áo phông bán được trong trường hợp đó.

c) Với giá bán như thế nào thì công ty sẽ đạt được ít nhất 675 triệu đồng doanh thu?

Lời giải:

a) Công thức biểu diễn doanh thu R là:

R(x) = n . x = (21 000 – 150x). x = – 150x² + 21 000x (nghìn đồng).

Hàm số xác định khi x ≥ 0 và n ≥ 0 (số lượng áo phông) ⇔ 21 000 – 150x ≥ 0 ⇔ x ≤ 140.

Vậy miền xác định của hàm số R(x) là D = [0; 140].

b) R(x) đạt cực đại tại x = $-\frac{b}{2a}=-\frac{21000}{2.\left(-150\right)}=70$ .

Khi đó R(70) = – 150 . 70² + 21 000 . 70 = 735 000.

Vậy công ty bán với giá 70 nghìn đồng mỗi chiếc áo thì doanh thu đạt cực đại là 735 000 nghìn đồng hay chính là 735 triệu đồng.

Số áo phông bán được trong trường hợp này là: n = 21 000 – 150 . 70 = 10 500 (chiếc).

c) Ta có: 675 triệu đồng = 675 000 nghìn đồng.

Xét bất phương trình – 150x² + 21 000x ≥ 675 000

⇔ – 150x² + 21 000x – 675 000 ≥ 0

⇔ 50 ≤ x ≤ 90.

Vậy với giá bán từ 50 nghìn đồng đến 90 nghìn đồng mỗi chiếc áo thì công ty sẽ đạt được ít nhất 675 triệu đồng doanh thu.

Bài 6 trang 71 SBT Toán 10 Tập 2: Người ta ước tính rằng trong khoảng từ năm 2010 đến năm 2030, số lượng điện thoại di động bán được của một công ty có thể được xấp xỉ bởi một hàm số bậc hai. Năm 2010 công ty đó bán được khoảng 19 nghìn chiếc điện thoại di động và năm 2019 bán được khoảng 100 nghìn chiếc điện thoại di động. Giả sử t là số năm tính từ năm 2010. Số điện thoại di động bán được năm 2010 được biểu diễn bởi điểm (0; 19) và số điện thoại di động bán được năm 2019 được biểu diễn bởi điểm (9; 100). Giả sử điểm (0; 19) là đỉnh đồ thị của hàm số bậc hai này.

a) Tìm hàm số bậc hai biểu diễn số điện thoại di động công ty đó bán được qua từng năm.

b) Dựa trên mô hình này, hãy tính số điện thoại di động bán được năm 2024.

c) Dựa trên mô hình này, hãy ước lượng xem khi nào thì số điện thoại di động bán được được vượt mức 300 nghìn chiếc.

Lời giải:

a) Giả sử y = at² + bt + c (a ≠ 0) là hàm số bậc hai mô tả lượng điện thoại di động bán được qua từng năm, trong đó t là số năm tính từ năm 2010.

Từ giả thiết ta có (0; 19) là đỉnh của đồ thị hàm số nên b = 0 và c = 19.

Điểm (9; 100) thuộc đồ thị hàm số nên ta có: 100 = a . 9² + 0 . 9 + 19 ⇔ a = 1.

Vậy hàm số cần tìm là: y = t² + 19.

b) Ta có: 2024 – 2010 = 14.

Do đó năm 2024 tương ứng với t = 14.

Khi đó, số lượng điện thoại di động bán được trong năm 2024 là:

y = 14² + 19 = 215 (nghìn chiếc).

c) Xét bất phương trình t² + 19 > 300.

Bất phương trình trên tương đương với t² – 281 > 0.

Nghiệm của phương trình t² – 281 = 0 là t ≈ – 16,8; t ≈ 16,8.

Khi đó t² – 281 > 0 ⇔ t < – 16,8 hoặc t > 16,8.

Do đó t ≥ 17.

Ta có: 2010 + 17 = 2027.

Vậy từ năm 2027 trở đi (đến năm 2030) thì số điện thoại di động bán được vượt 300 nghìn chiếc. 

Giải SBT Toán 10 trang 72 Tập 2

Bài 7 trang 72 SBT Toán 10 Tập 2: Tìm các giá trị của tham số m để hàm số $y=\sqrt{x^2+2mx-2m+3}$  có tập xác định là toàn bộ tập số thực ℝ.

Lời giải:

Hàm số đã cho có tập xác định là toàn bộ tập số thực ℝ khi và chỉ khi x² + 2mx – 2m + 3 ≥ 0 với mọi x ∈ ℝ.

Xét f(x) = x² + 2mx – 2m + 3 có ∆' = m² – 1 . (– 2m + 3) = m² + 2m – 3 và a = 1 > 0.

Ta có f(x) ≥ 0 với mọi x ∈ ℝ ⇔ ∆' ≤ 0 ⇔ m² + 2m – 3 ≤ 0 ⇔ – 3 ≤ m ≤ 1.

Vậy – 3 ≤ m ≤ 1 thì thỏa mãn yêu cầu bài toán.

Bài 8 trang 72 SBT Toán 10 Tập 2: Giải các phương trình chứa căn thức sau:

a) $\sqrt{3x^2-4x+1}=\sqrt{x^2-x}$ ;

b) $\sqrt{6x^2-11x-3}=2x-1$ .

Lời giải:

a) $\sqrt{3x^2-4x+1}=\sqrt{x^2-x}$

Bình phương hai vế của phương trình đã cho ta được:

3x² – 4x + 1 = x² – x

⇔ 2x² – 3x + 1 = 0

⇔ x = 1 hoặc x = $\frac{1}{2}$ .

Thử lại ta thấy phương trình đã cho có nghiệm duy nhất x = 1.

b) $\sqrt{6x^2-11x-3}=2x-1$

Bình phương hai vế của phương trình đã cho ta được:

6x² – 11x – 3 = (2x – 1)²

⇔ 6x² – 11x – 3 = 4x² – 4x + 1

⇔ 2x² – 7x – 4 = 0

⇔ x = 4 hoặc x = $-\frac{1}{2}$ .

Thử lại ta thấy phương trình đã cho có nghiệm duy nhất x = 4.

Bài 9 trang 72 SBT Toán 10 Tập 2: Đội văn nghệ của một trường trung học phổ thông gồm có 5 học sinh khối lớp 10, 5 học sinh khối lớp 11 và 5 học sinh khối lớp 12. Nhà trường cần chọn một đội gồm 10 học sinh để tham gia thi văn nghệ cấp huyện. Tính số cách lập đội văn nghệ sao cho có học sinh ở cả ba khối lớp và có nhiều nhất 2 học sinh khối lớp 10.

Lời giải:

Để lập đội văn nghệ gồm 10 học sinh ở cả ba khối và có nhiều nhất 2 học sinh khối lớp 10, ta thấy có 2 trường hợp: đội văn nghệ có đúng 1 học sinh khối lớp 10 và có đúng 2 học sinh khối lớp 10.

- Trường hợp 1: Có đúng 1 học sinh khối lớp 10.

Số cách chọn 1 học sinh khối lớp 10 trong 5 học sinh khối lớp 10 là: $C_5^1$  cách.

Chọn 9 bạn còn lại ở hai khối lớp 11 và 12, số cách chọn là: $C_{10}^9$  cách.

Vậy, theo quy tắc nhân, có $C_5^1.C_{10}^9$  = 5 . 10 = 50 cách lập đội văn nghệ trong trường hợp 1.

- Trường hợp 2: Có đúng 2 học sinh khối lớp 10.

Số cách chọn 2 học sinh khối lớp 10 trong 5 học sinh khối lớp 10 là: $C_5^2$  cách.

Chọn 8 bạn còn lại ở hai khối lớp 11 và 12, số cách chọn là: $C_{10}^8$  cách.

Vậy, theo quy tắc nhân, có $C_5^2.C_{10}^8$  = 10 . 45 = 450 cách lập đội văn nghệ trong trường hợp 2.

Vì hai trường hợp rời nhau nên theo quy tắc cộng, ta có số cách lập đội văn nghệ thỏa mãn yêu cầu của đề bài là: 50 + 450 = 500 (cách).

Bài 10 trang 72 SBT Toán 10 Tập 2: Viết khai triển nhị thức Newton của (3x – 2)ⁿ, biết n là số tự nhiên thoả mãn

$A_n^2+2C_n^1=30$.

Lời giải:

Ta có: $A_n^2+2C_n^1=30$

$$\begin{gathered} \iff \frac{n!}{\left(n-2\right)!}+2.\frac{n!}{1!.\left(n-1\right)!}=30 \\ \iff \frac{n\left(n-1\right)\left(n-2\right)!}{\left(n-2\right)!}+2\frac{n\left(n-1\right)!}{\left(n-1\right)!}=30 \end{gathered}$$

⇔ n(n – 1) + 2n = 30

⇔ n² + n – 30 = 0

⇔ n = 5 (thỏa mãn) hoặc n = – 6 (loại).

Vậy n = 5.

Khi đó ta có: (3x – 2)ⁿ = (3x – 2)⁵ = [3x + (– 2)⁵]

=$$\begin{gathered} C_5^0.{\left(3x\right)}^5+C_5^1.{\left(3x\right)}^4.\left(-2\right)+C_5^2.{\left(3x\right)}^3.{\left(-2\right)}^2 \\ +C_5^3.{\left(3x\right)}^2.{\left(-2\right)}^3+C_5^4.{\left(3x\right)}^1.{\left(-2\right)}^4+C_5^5.{\left(-2\right)}^5 \end{gathered}$$

= 243x⁵ – 810x⁴ + 1 080x³ – 720x² + 240x – 32.

Bài 11 trang 72 SBT Toán 10 Tập 2: Cho tam giác ABC có AB = 2, AC = 3, BC = 4.

a) Tính diện tích S của tam giác.

b) Tính bán kính đường tròn ngoại tiếp của tam giác.

Lời giải:

a) Nửa chu vi của tam giác ABC là:

p = (AB + AC + BC) : 2 = (2 + 3 + 4) : 2 = $\frac{9}{2}$  (đvđd).

Diện tích tam giác ABC là:

S =  $\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}$ (công thức Hê-rông)

=  $\sqrt{\frac{9}{2}.\left(\frac{9}{2}-2\right).\left(\frac{9}{2}-3\right).\left(\frac{9}{2}-4\right)}$  = $\frac{3\sqrt{15}}{4}$  (đvdt).

b) Gọi R là bán kính đường tròn ngoại tiếp của tam giác ABC.

Ta có: $S=\frac{AB.AC.BC}{4R}$

 $\Rightarrow R=\frac{AB.AC.BC}{4S}=\frac{\mathrm{2.3.4}}{4.\frac{3\sqrt{15}}{4}}=\frac{8\sqrt{15}}{15}$ (đvđd).

Bài 12 trang 72 SBT Toán 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho hai điểm A(3; 4), B(8; 6). Kẻ đường phân giác trong OD của tam giác OAB (D thuộc đoạn AB).

a) Tính OA, OB.

b) Chứng minh rằng $\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$ .

c) Tìm toạ độ điểm D.

Lời giải:

a) Ta có: A(3; 4), suy ra $\overrightarrow{OA}=\left(3;\text{\hspace{0.17em}\hspace{0.17em}}4\right)$ , do đó OA = $\sqrt{3^2+4^2}=5$ .

B(8; 6), suy ra $\overrightarrow{OB}=\left(8;6\right)$ , do đó OB = $\sqrt{8^2+6^2}$ = 10.

b) Do OD là đường phân giác trong của tam giác OAB nên theo tính chất đường phân giác ta có: $\frac{AD}{BD}=\frac{OA}{OB}=\frac{5}{10}=\frac{1}{2}$ .

Suy ra: BD = 2AD.

Mặt khác do D thuộc đoạn AB nên hai vectơ $\overrightarrow{AD},\overrightarrow{BD}$  ngược hướng.

Do vậy, $\overrightarrow{BD}=-2\overrightarrow{AD}$ .

Mà $\overrightarrow{BD}=\overrightarrow{OD}-\overrightarrow{OB}$ ; $\overrightarrow{AD}=\overrightarrow{OD}-\overrightarrow{OA}$ .

Từ đó ta có: $\overrightarrow{OD}-\overrightarrow{OB}=-2\left(\overrightarrow{OD}-\overrightarrow{OA}\right)$

$\iff 3\overrightarrow{OD}=2\overrightarrow{OA}+\overrightarrow{OB}$

$\iff \overrightarrow{OD}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$  (đpcm).

c) Gọi D(x; y), do $\overrightarrow{OD}=\frac{2}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}$ , suy ra: $\left\{\begin{array}{l}x=\frac{2}{3}{x}_A+\frac{1}{3}{x}_B\\ y=\frac{2}{3}{y}_A+\frac{1}{3}{y}_B\end{array}\right.$ .

$\Rightarrow \left\{\begin{array}{l}x=\frac{2}{3}.3+\frac{1}{3}.8=\frac{14}{3}\\ y=\frac{2}{3}.4+\frac{1}{3}.6=\frac{14}{3}\end{array}\right.$.

Vậy $D\left(\frac{14}{3};\frac{14}{3}\right)$ .

Bài 13 trang 72 SBT Toán 10 Tập 2: Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có M, N, P lần lượt là trung điểm của các đoạn thẳng BC, AC, AB. Biết rằng M(1; 2), N(0; –1) và P(–2; 3).

a) Lập phương trình tham số của đường thẳng BC.

b) Lập phương trình tổng quát của đường trung trực của đoạn thẳng BC.

Lời giải:

a) Do P và N lần lượt là trung điểm của AB và AC nên PN là đường trung bình của tam giác ABC, do đó PN // BC.

Ta có: $\overrightarrow{PN}=\left(2;-4\right)$

Do đó, một vectơ chỉ phương của đường thẳng BC là $\overrightarrow{u_{BC}}=\frac{1}{2}\overrightarrow{PN}=\frac{1}{2}\left(2;-4\right)=\left(1;-2\right)$ .

Mặt khác đường thẳng BC đi qua điểm M(1; 2) (do M là trung điểm của BC).

Vậy phương trình tham số của đường thẳng BC là: $\left\{\begin{array}{l}x=1+t\\ y=2-2t\end{array}\right.$ .

b) Gọi d là đường trung trực của đoạn thẳng BC.

Ta có d đi qua trung điểm M của BC và vuông góc với BC.

Do đó, $\overrightarrow{n_d}=\overrightarrow{u_{BC}}=\left(1;-2\right)$  là vectơ pháp tuyến của đường thẳng d.

Vậy phương trình tổng quát của đường thẳng d là:

1(x – 1) – 2(y – 2) = 0 hay x – 2y + 3 = 0.

Bài 14 trang 72 SBT Toán 10 Tập 2: Cho đường thẳng ∆: 3x + 4y – 25 = 0. Gọi (C) là đường tròn tâm O và tiếp xúc với ∆.

a) Viết phương trình đường tròn (C).

b) Tìm toạ độ tiếp điểm H của ∆ và (C).

Lời giải:

a) Do đường tròn (C) tiếp xúc với ∆ nên bán kính của đường tròn (C) bằng:

R = d(O, ∆) = $\frac{\left|3.0+4.0-25\right|}{\sqrt{3^2+4^2}}=\frac{25}{5}=5$ .

Vậy phương trình đường tròn (C) là: (x – 0)² + (y – 0)²  = 5² hay x² + y² = 25.

b) Vì ∆ tiếp xúc với (C) tại điểm H nên ta có OH ⊥ ∆. Do đó, $\overrightarrow{u_{OH}}=\overrightarrow{n_{\Delta }}=\left(3;4\right)$ .

Suy ra một vectơ pháp tuyến của đường thẳng OH là $\overrightarrow{n_{OH}}=\left(4;-3\right)$ .

Phương trình của đường thẳng OH là: 4(x – 0) – 3(y – 0) = 0 hay 4x – 3y = 0.

Vì H là giao điểm của ∆ và OH nên tọa độ của điểm H là nghiệm của hệ phương trình

$\left\{\begin{array}{l}3x+4y-25=0\\ 4x-3y=0\end{array}\right.\iff \left\{\begin{array}{l}x=3\\ y=4\end{array}\right.$.

Vậy H(3; 4).

Giải SBT Toán 10 trang 73 Tập 2

Bài 15 trang 73 SBT Toán 10 Tập 2: Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng toạ độ. Theo đó, tại thời điểm t (0 ≤ t ≤ 180), vật thể có vị trí toạ độ (4cos t°; 3sin t°).

a) Tìm vị trí ban đầu và vị trí kết thúc của vật thể.

b) Tìm quỹ đạo chuyển động của vật thể.

Lời giải:

a) Vị trí ban đầu của vật thể ứng với t = 0, suy ra vật thể ở vị trí có tọa độ là A₁(4; 0) (do 4cos 0° = 4 và 3sin 0° = 0).

Vị trí kết thúc của vật thể ứng với t = 180, suy ra vật thể ở vị trí có tọa độ là A₂(– 4; 0) (do 4cos 180° = – 4 và 3sin 180° = 0).

b) Vì vật thể có vị trí toạ độ (4cos t°; 3sin t°).

Do đó, với một điểm M bất kì thuộc quỹ đạo chuyển động của vật thể ta có:

x_M = 4cos t°, y_M = 3sin t°.

Khi đó từ đẳng thức: sin² t° + cos² t° = 1 hay (sin t°)² + (cos t°)² = 1, ta suy ra:

${\left(\frac{y_M}{3}\right)}^2+{\left(\frac{x_M}{4}\right)}^2=1\iff \frac{x_M^2}{16}+\frac{y_M^2}{9}=1$.

Do đó, vật thể chuyển động trên đường elip (E) có phương trình $\frac{x^2}{16}+\frac{y^2}{9}=1$ .

Khi t thay đổi trên đoạn [0; 180] thì sin t° thay đổi trên đoạn [0; 1] và cos t° thay đổi trên đoạn [– 1; 1]. Do đó, 4cos t° ∈ [– 4; 4] và 3sin t° ∈ [0; 3].

Vậy quỹ đạo vật thể (hay là tập hợp điểm M) là nửa đường elip (E) nằm trên trục hoành. 

Bài 16 trang 73 SBT Toán 10 Tập 2: Bảng sau đây cho biết lượng mưa trung bình hằng tháng tại Đà Nẵng và Hà Nội (mm).

 (Theo www.weatherspark.com)

a) Đà Nẵng hay Hà Nội có lượng mưa trung bình cả năm cao hơn?

b) Tính khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của hai mẫu số liệu về lượng mưa trung bình các tháng tại Đà Nẵng và Hà Nội. Nhận xét gì về sự phân tán của hai mẫu số liệu này?

Lời giải:

a) Lượng mưa trung bình cả năm của Đà Nẵng là:

$\overline{x}=$ (39,5 + 13,2 + 14,1 + 28,0 + 60,2 + 62,5 + 58,6 + 119,6 + 291,2 + 253,5 + 304,0 + 145,1) : 12 ≈ 115,79.

Lượng mưa trung bình cả năm của Hà Nội là:

$\overline{x^{\text{'}}}$ = (13,0 + 11,9 + 29,2 + 52,5 + 126,3 + 160,1 + 204,0 + 226,2 + 173,8 + 84,8 + 45,0 + 14,1) : 12 ≈ 95,08.

Vì 115,79 > 95,08.

Vậy Đà Nẵng có lượng mưa trung bình cả năm cao hơn Hà Nội.

b) Khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của hai mẫu số liệu về lượng mưa trung bình các tháng tại Đà Nẵng và Hà Nội.

* Đà Nẵng:

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

13,2; 14,1; 28,0; 39,5; 58,6; 60,2; 62,5; 119,6; 145,1; 253,5; 291,2; 304,0.   

Khoảng biến thiên: R = 304,0 – 13,2 = 290,8.

Trung vị: $Q_2=\frac{\mathrm{60,2}+\mathrm{62,5}}{2}=\mathrm{61,35}$ .

Tứ phân vị thứ nhất: Q₁ = $\frac{\mathrm{28,0}+\mathrm{39,5}}{2}=\mathrm{33,75}$ .

Tứ phân vị thứ ba: Q₃ = $\frac{\mathrm{145,1}+\mathrm{253,5}}{2}$ = 199,3.

Khoảng tứ phân vị: ∆_Q = Q₃ – Q₁ = 199,3 – 33,75 = 165,55.

Phương sai:

s² = [(115,79 – 13,2)² + (115,79 – 14,1)² + (115,79 – 28,0)² + (115,79 – 39,5)² + (115,79 – 58,6)² + (115,79 – 60,2)² + (115,79 – 62,5)² + (115,79 – 119,6)² + (115,79 – 145,1)² + (115,79 – 253,5)² + (115,79 – 291,2)² + (115,79 – 304,0)²] : 12 ≈ 10 801,91.  

Độ lệch chuẩn: s = $\sqrt{s^2}$ ≈ 103,93.

* Hà Nội:

Sắp xếp các số liệu theo thứ tự không giảm, ta được:

11,9; 13,0; 14,1; 29,2; 45,0; 52,5; 84,8; 126,3; 160,1; 173,8; 204,0; 226,2.

Khoảng biến thiên: R' = 226,2 – 11,9 = 214,3.

Trung vị: ${Q^{\text{'}}}_2=\frac{\mathrm{52,5}+\mathrm{84,8}}{2}=\mathrm{68,65}$ .

Tứ phân vị thứ nhất: Q'₁ = $\frac{\mathrm{14,1}+\mathrm{29,2}}{2}=\mathrm{21,65}$ .

Tứ phân vị thứ ba: Q'₃ = $\frac{\mathrm{160,1}+\mathrm{173,8}}{2}$ = 166,95.

Khoảng tứ phân vị: ∆'_Q = Q'₃ – Q'₁ = 166,95 – 21,65 = 145,3.

Phương sai:

s'² = [(95,08 – 11,9)² + (95,08 – 13,0)² + (95,08 – 14,1)² + (95,08 – 29,2)² + (95,08 – 45,0)² + (95,08 – 52,5)² + (95,08 – 84,8)² + (95,08 – 126,3)² + (95,08 – 160,1)² + (95,08 – 173,8)² + (95,08 – 204,0)² + (95,08 – 226,2)²] : 12 ≈ 5 786,32.  

Độ lệch chuẩn: s' = $\sqrt{{s^{\text{'}}}^2}$ ≈ 76,07.

Từ đó ta có dãy số liệu về lượng mưa trung bình các tháng tại Đà Nẵng phân tán hơn so với tại Hà Nội.

Bài 17 trang 73 SBT Toán 10 Tập 2: Khi tham gia một trò chơi quay số trúng thưởng, mỗi người chơi chọn một số 4 chữ số (có tính cả số 0 ở đầu). Bạn An chọn số 0347. Người quản trò quay 4 tấm bìa cứng hình tròn I, II, III, IV, mỗi tấm bìa được chia thành 10 phần có diện tích bằng nhau và đánh số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 được gắn vào trục quay có mũi tên ở tâm. Giả sử mũi tên của bìa cứng số I, II, III và IV tương ứng dừng ở các số a, b, c, d. Khi đó số $\overline{abcd}$  gọi là số trúng thưởng. Nếu số của người chơi trùng hoàn toàn với số trúng thưởng thì người chơi trúng giải nhất; trùng với 3 chữ số của số trúng thưởng (tính cả thứ tự) thì người chơi trúng giải nhì.

Tính xác suất bạn An trúng giải nhất, giải nhì.

Lời giải:

Không gian mẫu: Ω = { $\overline{abcd}$; a, b, c, d ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}}.

Theo quy tắc nhân, ta có n(Ω) = 10⁴. (Do có 10 cách chọn mỗi số a, b, c, d).

+) Gọi E là biến cố “An trúng giải nhất”. Khi đó E = {0347}, n(E) = 1.

Vậy xác suất để An trúng giải nhất là P(E) = $\frac{n\left(E\right)}{n\left(\Omega \right)}=\frac{1}{{10}^4}$ .

+) Gọi F là biến cố “An trúng giải nhì”.

Khi đó, F = { $\overline{a347};\overline{0b47};\overline{03c7};\overline{034d}$| a ∈ {1; 2; 3; 4; 5; 6; 7; 8; 9}, b ∈ {0; 1; 2; 4; 5; 6; 7; 8; 9}, c ∈ {0; 1; 2; 3; 5; 6; 7; 8; 9}, d ∈ {0; 1; 2; 3; 4; 5; 6; 8; 9}}.

Mỗi cách chọn a, b, c, d thỏa mãn F là chọn 1 trong 9 số. Có 9 cách chọn a, 9 cách chọn b, 9 cách chọn c, 9 cách chọn d.

Mỗi trường hợp là rời nhau nên theo quy tắc cộng ta có n(F) = 9 + 9 + 9 + 9 = 36.

Vậy xác suất để An trúng giải nhì là P(F) = $\frac{n\left(F\right)}{n\left(\Omega \right)}=\frac{36}{{10}^4}=\mathrm{0,0036}$ .

Bài 18 trang 73 SBT Toán 10 Tập 2: Khi tham gia một trò chơi bốc thăm trúng thưởng, mỗi người chơi chọn một bộ 6 số đôi một khác nhau từ 45 số: 1; 2;....; 45, chẳng hạn bạn Bình chọn bộ số {4; 12; 20; 31; 32; 33}. Sau đó, người quản trò bốc thăm ngẫu nhiên 6 quả bóng (không hoàn lại) từ một thùng kín đựng 45 quả bóng như nhau ghi các số 1; 2; ...; 45. Bộ 6 số ghi trên 6 quả bóng đó, gọi là bộ số trúng thưởng. Nếu bộ số của người chơi trùng với 4 số của bộ số trúng thưởng thì người chơi trúng giải nhì. Tính xác suất bạn Bình trúng giải nhì khi chơi.

Lời giải:

Không gian mẫu Ω là tập hợp tất cả các tập con có 6 phần tử của tập {1; 2;....; 44; 45}.

Do đó, n(Ω) = $C_{45}^6$ .

Gọi E là biến cố: “Bạn Bình trúng giải nhì”.

E là tập hợp tất cả các tập con gồm 6 phần tử của tập {1; 2;....; 44; 45} có tính chất:

- Bốn phần tử của nó thuộc tập {4; 12; 20; 31; 32; 33};

- Hai phần tử còn lại không thuộc tập {4; 12; 20; 31; 32; 33}.

Mỗi phần tử của E được hình thành từ hai công đoạn.

Công đoạn 1: Chọn 4 phần tử trong tập {4; 12; 20; 31; 32; 33}. Có  cách chọn.

Công đoạn 2: Chọn 2 phần tử còn lại trong 39 phần tử của tập {1; 2; ....; 44; 45} \ {4; 12; 20; 31; 32; 33}. Có $C_{39}^2=741$  cách chọn.

Theo quy tắc nhân, tập E có 15 . 741 = 11 115 phần tử. Vậy n(E) = 11 115.

Vậy xác suất bạn Bình trúng giải nhì khi chơi là:

P(E) = $\frac{n\left(E\right)}{n\left(\Omega \right)}=\frac{11115}{C_{45}^6}=\frac{11115}{8145060}\approx \mathrm{0,001365}$ .

Xem thêm lời giải sách bài tập Toán lớp 10 Kết nối tri thức với cuộc sống hay, chi tiết khác: 

Bài 25: Nhị thức Newton

Ôn tập chương 8

Bài 26: Biến cố và định nghĩa cổ điển của xác suất

Bài 27: Thực hành tính xác suất theo định nghĩa cổ điển

Bài tập cuối chương 9