Với vecto u khác vecto 0 và hai số thực k, t, những khẳng định nào sau đây là đúng?
239
24/05/2023
HĐ 3 trang 57 Toán 10 Tập 1: Với →u≠→0 và hai số thực k, t, những khẳng định nào sau đây là đúng?
a) Hai vectơ k(t→u) và (kt)→u có cùng độ dài bằng |kt||→u|.
b) Nếu kt ≥ 0 thì cả hai vectơ k(t→u),(kt)→u cùng hướng với →u.
c) Nếu kt < 0 thì cả hai vectơ k(t→u),(kt)→u ngược hướng với →u.
d) Hai vectơ k(t→u) và (kt)→u bằng nhau.
Trả lời
a) Ta có: |k(t→u)|=|k||t→u|=|k||t||→u|=|kt||→u| và |(kt)→u|=|kt||→u|
Suy ra |k(t→u)|=|(kt)→u|=|kt||→u|
Do đó hai vectơ k(t→u) và (kt)→u có cùng độ dài bằng |kt||→u|.
Vậy khẳng định a) đúng.
b) - Với kt ≥ 0 thì vectơ (kt)→u cùng hướng với vectơ →u
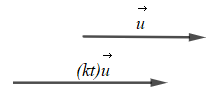
- Với kt ≥ 0 ⇔{k≥0t≥0 hoặc {k≤0t≤0
+) Trường hợp 1: k ≥ 0 và t ≥ 0
Với t ≥ 0 thì vectơ t→u cùng hướng với vectơ →u;
Với k ≥ 0 thì vectơ k(t→u)cùng hướng với vectơ t→u;
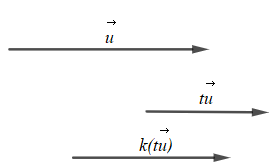
Do đó với k ≥ 0 và t ≥ 0 thì k(t→u) cùng hướng với vectơ →u(do cùng hướng với t→u).
+) Trường hợp 2: k ≤ 0 và t ≤ 0
Với t ≤ 0 thì vectơ t→u ngược hướng với vectơ →u;
Với k ≤ 0 thì vectơ k(t→u) ngược hướng với vectơ t→u;
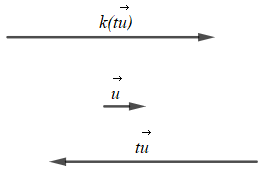
Do đó với k ≤ 0 và t ≤ 0 thì k(t→u) cùng hướng với vectơ →u(do cùng ngược hướng với t→u).
Kết hợp hai trường hợp ta có: với kt ≥ 0 thì k(t→u) cùng hướng với vectơ →u.
Suy ra: nếu kt ≥ 0 thì cả hai vecto k(t→u),(kt)→u cùng hướng với →u.
Vậy khẳng định b) là đúng.
c) – Với kt < 0 thì vectơ (kt)→u ngược hướng với vectơ →u
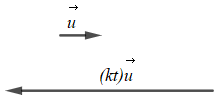
- Với kt < 0 ⇔{k>0t<0 hoặc {k<0t>0
+) Trường hợp 1: k > 0 và t < 0
Với t < 0 thì vectơ t→u ngược hướng với vectơ →u;
Với k > 0 thì vectơ k(t→u)cùng hướng với vectơ t→u;
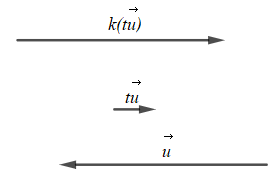
Do đó với k > 0 t < 0 thì k(t→u) ngược hướng với vectơ →u
+) Trường hợp 2: k < 0 và t > 0
Với t > 0 thì vectơ t→u cùng hướng với vectơ →u;
Với k < 0 thì vectơ k(t→u) ngược hướng với vectơ t→u;
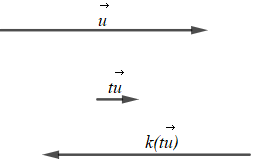
Do đó với k < 0 và t > 0 thì k(t→u) ngược hướng với vectơ →u.
Kết hợp hai trường hợp ta có: với kt < 0 thì k(t→u) ngược hướng với vectơ →u.
Suy ra nếu kt < 0 thì cả hai vectơ k(t→u),(kt)→u ngược hướng với →u.
Vậy khẳng định c) là đúng.
d) Theo câu a thì hai vectơ k(t→u) và (kt)→u có cùng độ dài.
+ Nếu kt ≥ 0 thì cả hai vectơ k(t→u),(kt)→u cùng hướng với →u.
Suy ra hai vectơ k(t→u),(kt)→u cùng hướng.
+ Nếu kt < 0 thì cả hai vectơ k(t→u),(kt)→u ngược hướng với →u.
Suy ra hai vectơ k(t→u),(kt)→u cùng hướng.
Do đó hai vectơ k(t→u),(kt)→u cùng hướng với mọi k, t.
⇒k(t→u)=(kt)→u
Hay hai vectơ k(t→u) và (kt)→u bằng nhau.
Vậy khẳng định d) đúng.
Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:
Bài 7: Các khái niệm mở đầu
Bài 8: Tổng và hiệu của hai vectơ
Bài 9: Tích của một vecto với một số
Bài 10: Vectơ trong mặt phẳng tọa độ
Bài 11: Tích vô hướng của hai vecto
Bài tập cuối chương 4






