Cho hai điểm phân biệt A và B. Hãy xác định điểm K sao cho

Bài 4.13 trang 58 Toán 10 Tập 1: Cho hai điểm phân biệt A và B.

a) Hãy xác định điểm K sao cho $\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}.$

b) Chứng minh rằng với mọi điểm O, ta có: $\overrightarrow{OK}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}.$

$\overrightarrow{OK}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}.$

Trả lời

a) Cách 1:

Giả sử có điểm K thỏa mãn $\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}$. Khi đó $\overrightarrow{KA}=-2\overrightarrow{KB}$. Suy ra hai vectơ $\overrightarrow{KA}$ và $\overrightarrow{KB}$ cùng phương, ngược hướng và KA = 2KB. Suy ra điểm K thuộc đoạn AB và KA = 2KB.

Cách 2:

Gọi M là trung điểm của đoạn thẳng AB suy ra $\overrightarrow{MA}+\overrightarrow{MB}=\overrightarrow{0}$.

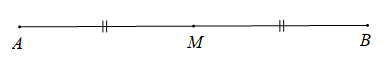
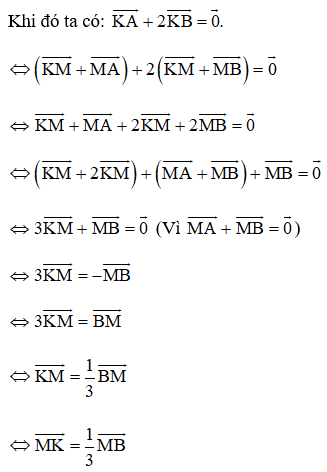
Suy ra vecto $\overrightarrow{MK}$ cùng hướng với vectơ $\overrightarrow{MB}$ và thỏa mãn $MK=\frac{1}{3}MB.$

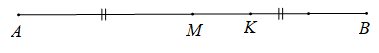
Vậy điểm K là điểm nằm giữa M và B sao cho thỏa mãn $MK=\frac{1}{3}MB.$

b)

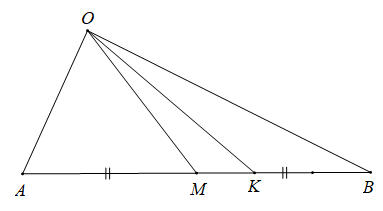
Cách 1:

Ta có:  

$$\begin{gathered} \frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}=\frac{1}{3}\left(\overrightarrow{OK}+\overrightarrow{KA}\right)+\frac{2}{3}\left(\overrightarrow{OK}+\overrightarrow{KB}\right) \\ =\frac{1}{3}\overrightarrow{OK}+\frac{1}{3}\overrightarrow{KA}+\frac{2}{3}\overrightarrow{OK}+\frac{2}{3}\overrightarrow{KB} \\ =\left(\frac{1}{3}\overrightarrow{OK}+\frac{2}{3}\overrightarrow{OK}\right)+\left(\frac{1}{3}\overrightarrow{KA}+\frac{2}{3}\overrightarrow{KB}\right) \\ =\overrightarrow{OK}+\frac{1}{3}\left(\overrightarrow{KA}+2\overrightarrow{KB}\right) \end{gathered}$$ 

Mà $\overrightarrow{KA}+2\overrightarrow{KB}=\overrightarrow{0}$ (theo câu a) do đó $\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}=\overrightarrow{OK}+\frac{1}{3}.\overrightarrow{0}=\overrightarrow{OK}$ 

Vậy với mọi điểm O, ta có:  $\overrightarrow{OK}=\frac{1}{3}\overrightarrow{OA}+\frac{2}{3}\overrightarrow{OB}.$

Cách 2:

Ta có: $\overrightarrow{OK}=\overrightarrow{OM}+\overrightarrow{MK}$

Theo câu a ta có $\overrightarrow{MK}=\frac{1}{3}\overrightarrow{MB}=\frac{1}{3}\left(\overrightarrow{MO}+\overrightarrow{OB}\right)$

Do đó 

$$\begin{gathered} \overrightarrow{OK}=\overrightarrow{OM}+\overrightarrow{MK}= \\ \overrightarrow{OM}+\frac{1}{3}\left(\overrightarrow{MO}+\overrightarrow{OB}\right) \\ =\overrightarrow{OM}+\frac{1}{3}\overrightarrow{MO}+\frac{1}{3}\overrightarrow{OB} \\ =\overrightarrow{OM}-\frac{1}{3}\overrightarrow{OM}+\frac{1}{3}\overrightarrow{OB} \\ =\frac{2}{3}\overrightarrow{OM}+\frac{1}{3}\overrightarrow{OB} \end{gathered}$$

Vì M là trung điểm của AB nên

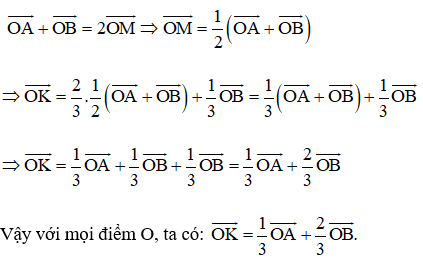
Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto

Bài tập cuối chương 4