Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị vecto AM theo hai vecto AB và AD

Bài 4.11 trang 58 Toán 10 Tập 1: Cho hình bình hành ABCD. Gọi M là trung điểm cạnh BC. Hãy biểu thị vecto AM theo hai vecto AB và AD

Trả lời

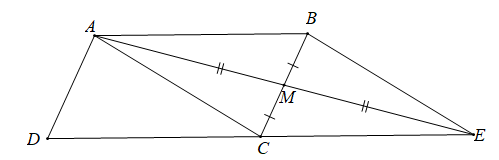
Gọi E là điểm đối xứng với A qua M.

Khi đó M là trung điểm của BC và AE.

Suy ra tứ giác ABEC là hình bình hành.

$\Rightarrow \overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AE}$ (quy tắc hình bình hành)

Mà $\overrightarrow{AE}=2\overrightarrow{AM}$ (M là trung điểm của AE)

$\Rightarrow \overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AM}\Rightarrow \overrightarrow{AM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$

Xét hình bình hành ABCD có: $\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$ (quy tắc hình bình hành)

$\Rightarrow \overrightarrow{AM}=\frac{\overrightarrow{AB}+\left(\overrightarrow{AB}+\overrightarrow{AD}\right)}{2}=\frac{\overrightarrow{AB}+\overrightarrow{AB}+\overrightarrow{AD}}{2}$

$\Rightarrow \overrightarrow{AM}=\frac{2\overrightarrow{AB}+\overrightarrow{AD}}{2}=\frac{2\overrightarrow{AB}}{2}+\frac{\overrightarrow{AD}}{2}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}$

Vậy $\overrightarrow{AM}=\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AD}.$

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto

Bài tập cuối chương 4