Giải SGK Toán 10 (Kết nối tri thức) Bài 8: Tổng và hiệu của hai vectơ

Giải Toán 10 Bài 8 : Tổng và hiệu của hai vectơ

Mở đầu

Mở đầu trang 51 Toán 10 Tập 1: Một con tàu chuyển động từ bờ bên này sang bờ bên kia của một dòng sông với vận tốc riêng không đổi. Giả sử vận tốc dòng nước là không đổi và đáng kể, các yếu tố bên ngoài khác không ảnh hưởng đến vận tốc thực tế của tàu. Nếu không quan tâm đến điểm đến thì cần giữ lái cho tàu tạo với bờ sông một góc bao nhiêu để tàu sang bờ bên kia được nhanh nhất?

Lời giải

Sau bài học này ta sẽ giải quyết bài toán này như sau:

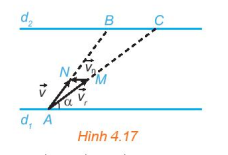
Ta biểu thị hai bờ sông là hai đường thẳng song song d₁, d₂ (H.4.17).

Giả sử tàu xuất phát từ $A\in d_1$ và bánh lái luôn được giữ để tàu tạo với bờ một góc $\alpha$.

Gọi $\overrightarrow{v_r}$ và $\overrightarrow{v_n}$ lần lượt là vận tốc riêng của tàu và vận tốc dòng nước.

Gọi M, N là các điểm sao cho $\overrightarrow{v_r}=\overrightarrow{AM},\overrightarrow{v_n}=\overrightarrow{MN}.$

Khi đó tàu chuyển động với vectơ vận tốc thực tế là $\overrightarrow{v}=\overrightarrow{v_r}+\overrightarrow{v_n}=\overrightarrow{AM}+\overrightarrow{MN}=\overrightarrow{AN}.$

Gọi B, C tương ứng là giao điểm của AN, AM với d₂.

Tàu chuyển động thẳng từ A đến B với vận tốc thực tế là $\overrightarrow{AN}$, do đó thời gian cần thiết để tàu sang được bờ d₂ là $\frac{AB}{AN}=\frac{AC}{AM}$.

Mặt khác, $AM=\left|\overrightarrow{v_r}\right|$ không đổi nên $\frac{AC}{AM}$ nhỏ nhất $\iff$ AC nhỏ nhất $\iff AC\perp d_2\iff AM\perp d_2.$

Vậy để tàu sang được bờ bên kia nhanh nhất, ta giữ bánh lái để tàu luôn vuông góc với bờ.

1. Tổng của hai vecto

Giải Toán 10 trang 51 Tập 1

HĐ 1 trang 51 Toán 10 Tập 1: Với hai vectơ $\overrightarrow{a},\overrightarrow{b}$ cho trước, lấy một điểm A và vẽ các vectơ $\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{BC}=\overrightarrow{b}.$ Lấy một điểm A' khác A cũng vẽ các vectơ $\overrightarrow{A\text{'}B\text{'}}=\overrightarrow{a},\overrightarrow{B\text{'}C\text{'}}=\overrightarrow{b}.$ Hỏi hai vectơ $\overrightarrow{AC},\overrightarrow{A\text{'}C\text{'}}$ có mối quan hệ gì?

Lời giải

HĐ 2 trang 51 Toán 10 Tập 1: Cho hình bình hành ABCD. Tìm mối quan hệ giữa hai vectơ $\overrightarrow{AB}+\overrightarrow{AD}$ và $\overrightarrow{AC}$.

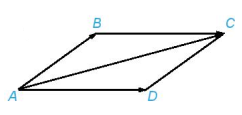
Lời giải

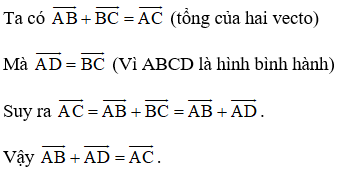
Giải Toán 10 trang 52 Tập 1

HĐ 3 trang 52 Toán 10 Tập 1:

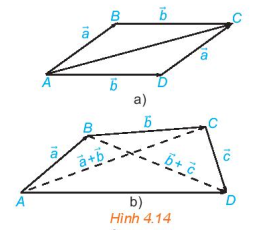
a) Trong Hình 4.14a, hãy chỉ ra vectơ $\overrightarrow{a}+\overrightarrow{b}$ và vectơ $\overrightarrow{b}+\overrightarrow{a}$.

b) Trong Hình 4.14b, hãy chỉ ra vectơ $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}$ và vectơ $\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)$.

Lời giải

+ Trong Hình 4.14a ta có: $\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ và $\overrightarrow{b}+\overrightarrow{a}=\overrightarrow{AD}+\overrightarrow{DC}=\overrightarrow{AC}$.

+ Trong Hình 4.14b ta có: $\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}=\overrightarrow{AC}+\overrightarrow{CD}=\overrightarrow{AD}$ và $\overrightarrow{a}+\left(\overrightarrow{b}+\overrightarrow{c}\right)=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}$.

Luyện tập 1 trang 52 Toán 10 Tập 1: Cho hình thoi ABCD với cạnh có độ dài bằng 1 và $\widehat{BAD}=120°$. Tính độ dài của các vectơ $\overrightarrow{CB}+\overrightarrow{CD},\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA}$

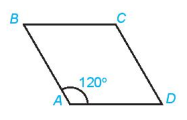
Lời giải

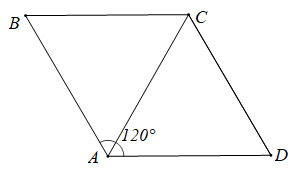
+ Tứ giác ABCD là hình thoi nên ABCD cũng là hình bình hành

Do đó $\overrightarrow{CB}+\overrightarrow{CD}=\overrightarrow{CA}$ (quy tắc hình bình hành)

$\Rightarrow \left|\overrightarrow{CB}+\overrightarrow{CD}\right|=\left|\overrightarrow{CA}\right|=CA$

ABCD là hình thoi nên AB = BC và AC là tia phân giác $\widehat{BAD}$ (tính chất hình thoi)

$\Rightarrow \widehat{BAC}=\widehat{CAD}=\frac{\widehat{BAD}}{2}$$=\frac{120°}{2}=60°$

Xét ΔABC có AB = BC và $\widehat{BAC}=60°$ 

⇒ ΔABC đều

⇒ AC = AB = BC = 1

Suy ra $\left|\overrightarrow{CB}+\overrightarrow{CD}\right|=1.$

+ Ta có:

$$\begin{gathered} \overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA}=\overrightarrow{CD}+\overrightarrow{DB}+\overrightarrow{BA} \\ =\left(\overrightarrow{CD}+\overrightarrow{DB}\right)+\overrightarrow{BA}=\overrightarrow{CB}+\overrightarrow{BA}=\overrightarrow{CA} \end{gathered}$$

 (quy tắc ba điểm).

$\Rightarrow \left|\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA}\right|=\left|\overrightarrow{CA}\right|=CA=1$

Vậy độ dài của các vectơ $\overrightarrow{CB}+\overrightarrow{CD}$ và $\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BA}$ đều bằng 1.

2. Hiệu của hai vecto

HĐ 4 trang 52 Toán 10 Tập 1: Thế nào là hai lực cân bằng? Nếu dùng hai vectơ để biểu diễn hai lực cân bằng thì hai vectơ này có mối quan hệ gì với nhau?

Lời giải

Nếu chỉ có hai lực tác dụng vào cùng một vật mà vật vẫn đứng yên thì hai lực đó là hai lực cân bằng.

Ví dụ: Hai đội kéo co cùng kéo sợi dây. Nếu hai đội mạnh ngang nhau thì họ sẽ tác dụng lên dây hai lực cân bằng. Sợi dây chịu tác dụng của hai lực cân bằng thì sẽ đứng yên.

Hai vectơ $\overrightarrow{F_1}$ và $\overrightarrow{F_2}$ biểu diễn cho hai vectơ cân bằng thì hai vectơ này có chung gốc, cùng phương, ngược hướng và có độ lớn (hay độ dài) bằng nhau.

Giải Toán 10 trang 53 Tập 1

Luyện tập 2 trang 53 Toán 10 Tập 1: Cho tứ giác ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và O là trung điểm của MN. Chứng minh rằng $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$.

Lời giải

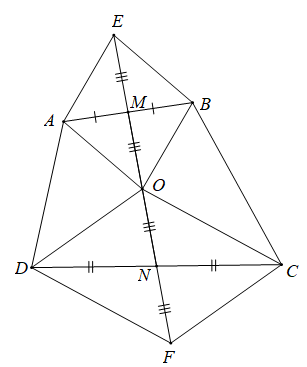
Gọi E và F lần lượt là điểm đối xứng với O qua M và N.

Suy ra M là trung điểm của AB và EO; N là trung điểm của DC và OF.

Khi đó các tứ giác OAEB và OCFD là các hình bình hành

$\Rightarrow \overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OE}$ (quy tắc hình bình hành trong hình bình hành OAEB)

Và $\overrightarrow{OD}+\overrightarrow{OC}=\overrightarrow{OF}$ (quy tắc hình bình hành trong hình bình hành OCFD).

$\Rightarrow \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{OE}+\overrightarrow{OF}$ 

Vì O là trung điểm của MN nên OM = ON, mà OM = ME, ON = NF.

Do đó OE = OF.

Suy ra hai vectơ $\overrightarrow{OE}$ và $\overrightarrow{OF}$ có cùng độ dài và ngược hướng nên chúng là hai vectơ đối nhau, do đó $\overrightarrow{OE}+\overrightarrow{OF}=\overrightarrow{0}$

$\Rightarrow \overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{0}$.

Giải Toán 10 trang 54 Tập 1

Vận dụng trang 54 Toán 10 Tập 1: Tính lực kéo cần thiết để kéo một khẩu pháo có trọng lượng 22 148N (ứng với khối lượng xấp xỉ 2 260kg) lên một con dốc nghiêng 30° so với phương nằm ngang (H.4.18). Nếu lực kéo của mỗi người bằng 100 N thì cần tối thiểu bao nhiêu người để kéo pháo?

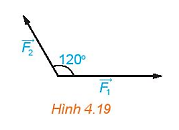
Chú ý: Ta coi khẩu pháo chịu tác động của ba lực: trọng lực $\overrightarrow{P}$ (có độ lớn $\left|\overrightarrow{P}\right|=22148N,$ có phương vuông góc với phương nằm ngang và hướng xuống dưới), phản lực $\overrightarrow{\text{W}}$ (có độ lớn $\left|\overrightarrow{\text{W}}\right|=\left|\overrightarrow{P}\right|cos30°$, có phương vuông góc với mặt dốc và hướng lên trên) và lực kéo $\overrightarrow{F}$(theo phương dốc, hướng từ chân dốc lên đỉnh dốc).

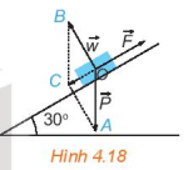
Lời giải

Do khẩu pháo chịu tác động của ba lực: trọng lực $\overrightarrow{P}$, phản lực $W$ và lực kéo $\overrightarrow{F}$. Để kéo được khẩu pháo đi lên ta cần lực kéo $\overrightarrow{F}$ có độ lớn lớn hơn độ lớn của tổng hai lực $\overrightarrow{P}$ và $\overrightarrow{\text{W}}$, tức là: $\left|\overrightarrow{F}\right|>\left|\overrightarrow{\text{W}}+\overrightarrow{P}\right|$ 

Xét hình bình hành OACB có $\overrightarrow{\text{W}}+\overrightarrow{P}=\overrightarrow{OC}$ suy ra $\left|\overrightarrow{\text{W}}+\overrightarrow{P}\right|=\left|\overrightarrow{OC}\right|$

Xét ΔOBC vuông tại O, có:

$OC=BC.\sin 30°$$=\left|P\right|\sin 30°.$

Do đó $\left|\overrightarrow{\text{W}}+\overrightarrow{P}\right|=\left|\overrightarrow{OC}\right|=\left|\overrightarrow{P}\right|.\sin 30°=22 148.\frac{1}{2}=11 074$ (N)

$\Rightarrow \left|\overrightarrow{F}\right|>11074N$

Ta có: 11 074 : 100 = 110,74 

Nếu lực kéo của mỗi người bằng 100 N thì cần tối thiểu số người để kéo pháo là 111 người.

Vậy ta cần một lực kéo lớn hơn 11 074 N để kéo khẩu pháo đi lên và nếu lực kéo của mỗi người bằng 100 N thì cần tối thiểu 111 người để kéo pháo lên.

Bài tập

Bài 4.6 trang 54 Toán 10 Tập 1: Cho bốn điểm A, B, C, D. Chứng minh rằng:

a) $\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}=\overrightarrow{0};$

b) $\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{BC}-\overrightarrow{BD};$

Lời giải

a) Ta có:

$$\begin{gathered} \overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA} \\ =\left(\overrightarrow{AB}+\overrightarrow{BC}\right)+\left(\overrightarrow{CD}+\overrightarrow{DA}\right) \\ =\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{AA}=\overrightarrow{0} \end{gathered}$$

(quy tắc ba điểm).

b) Ta có: $\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{DC}$ (quy tắc hiệu)

$\overrightarrow{BC}-\overrightarrow{BD}=\overrightarrow{DC}$ (quy tắc hiệu)

$\Rightarrow \overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{BC}-\overrightarrow{BD}.$

Bài 4.7 trang 54 Toán 10 Tập 1: Cho hình bình hành ABCD. Hãy tìm điểm M để $\overrightarrow{BM}=\overrightarrow{AB}+\overrightarrow{AD}$. Tìm mối quan hệ giữa hai vecto $\overrightarrow{CD}$ và $\overrightarrow{CM}$.

Lời giải

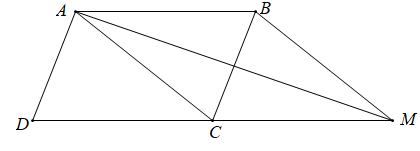
Vì ABCD là hình bình hành nên $\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ (quy tắc hình bình hành)

Theo đề bài $\overrightarrow{BM}=\overrightarrow{AB}+\overrightarrow{AD}$, do đó ta cần tìm điểm M thỏa mãn $\overrightarrow{AC}=\overrightarrow{BM}$ 

⇔ ACMB là hình bình hành

Vậy điểm M cần tìm là đỉnh thứ tư của hình bình hành dựng trên hai cạnh AB, AC.

Do tứ giác ACMB là hình bình hành

Bài 4.8 trang 54 Toán 10 Tập 1: Cho tam giác đều ABC có cạnh bằng a. Tính độ dài các vectơ $\overrightarrow{AB}-\overrightarrow{AC},\overrightarrow{AB}+\overrightarrow{AC}$.

Lời giải

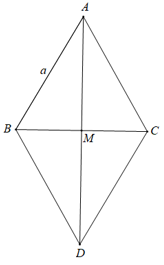
Ta có: $\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CB}$ (quy tắc hiệu)

Suy ra $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CB}\right|=CB=a.$ 

Gọi D là điểm thoả mãn điều kiện ABDC là hình hình hành.

 $\Rightarrow \overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AD}$ (quy tắc hình bình hành)

$\Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AC}\right|=\left|\overrightarrow{AD}\right|=AD$

Gọi M là giao điểm của AD và BC

⇒ M là trung điểm của BC và AD (tính chất hình bình hành)

AM vừa là đường trung tuyến vừa là đường cao của tam giác đều ABC.

Do đó tam giác ABM vuông tại M có AB = a, BM = $\frac{1}{2}BC=\frac{1}{2}a$, áp dụng định lí Pythagore ta có: AB² = AM² + BM²

⇒ AM² = AB² – BM² = $a^2-{\left(\frac{1}{2}a\right)}^2=a^2-\frac{1}{4}{a}^2=\frac{3a^2}{4}$

$\Rightarrow AM=\frac{a\sqrt{3}}{2}$
Mà M là trung điểm của AD nên AD = 2AM $=2.\frac{a\sqrt{3}}{2}=a\sqrt{3}$

$\Rightarrow \left|\overrightarrow{AB}+\overrightarrow{AC}\right|=AD=a\sqrt{3}$

Vậy $\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=a$ và $\left|\overrightarrow{AB}+\overrightarrow{AC}\right|=a\sqrt{3}$.

Bài 4.9 trang 54 Toán 10 Tập 1: Hình 4.19 biểu diễn hai lực $\overrightarrow{F_1},\overrightarrow{F_2}$ cùng tác động lên một vật, cho $\left|\overrightarrow{F_1}\right|=3N,\left|\overrightarrow{F_2}\right|=2N.$ Tính độ lớn của hợp lực $\overrightarrow{F_1}+\overrightarrow{F_2}$.

Lời giải

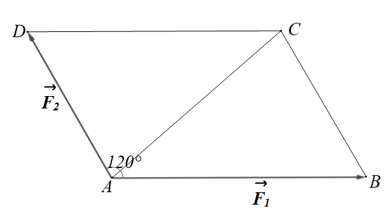
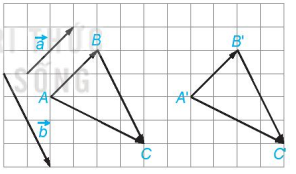
Vẽ điểm D sao cho ABCD là hình bình hành trong đó $\overrightarrow{AB}$ biểu diễn $\overrightarrow{F_1}$; $\overrightarrow{AD}$ biểu diễn $\overrightarrow{F_2}$ và $\widehat{BAD}=120°$ (như hình vẽ trên).

Suy ra $\overrightarrow{F_1}+\overrightarrow{F_2}=\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$ (quy tắc hình bình hành)

Do đó $\left|\overrightarrow{F_1}+\overrightarrow{F_2}\right|=\left|\overrightarrow{AC}\right|=AC$

Xét tam giác ABC, áp dụng định lí côsin ta có:

AC² = AB² + BC² – 2.AB.BC.cos$\widehat{ABC}$ 

+) $AB=\left|\overrightarrow{AB}\right|=\left|\overrightarrow{F_1}\right|$ mà $\left|\overrightarrow{F_1}\right|=3$ nên AB = 3

+) Vì ABCD là hình bình hành nên BC = AD (tính chất hình bình hành)

Mà AD = $\left|\overrightarrow{AD}\right|=\left|\overrightarrow{F_2}\right|=2$ 

Do đó BC = 2.

+) Vì ABCD là hình bình hành nên AD // BC do đó $\widehat{ABC}+\widehat{BAD}={180}^0$ (hai góc trong cùng phía)

Suy ra $\widehat{ABC}=180°-\widehat{BAD}=180°-120°=60°$ 

+) Ta có AC² = AB² + BC² – 2.AB.BC.cos$\widehat{ABC}$ 

AC² = 3² + 2² – 2.3.2.cos 60°

AC² = 7

$\Rightarrow AC=\sqrt{7}$

$\Rightarrow \left|\overrightarrow{F_1}+\overrightarrow{F_2}\right|=\sqrt{7}$

Vậy độ lớn của hợp lực $\overrightarrow{F_1}+\overrightarrow{F_2}$ là $\sqrt{7}$(N).

Bài 4.10 trang 54 Toán 10 Tập 1: Hai con tàu xuất phát cùng lúc từ bờ bên này sang bờ bên kia của dòng sông với vận tốc riêng không đổi và có độ lớn bằng nhau. Hai tàu luôn giữ được lái sao cho chúng tạo với bờ cùng một  góc nhọn nhưng một tàu hướng xuống hạ lưu, một tàu hướng lên thượng nguồn (hình bên). Vận tốc dòng nước là đáng kể, các yếu tố bên ngoài khác không ảnh hưởng tới vận tốc của các tàu. Hỏi tàu nào sang bờ bên kia trước?

Lời giải

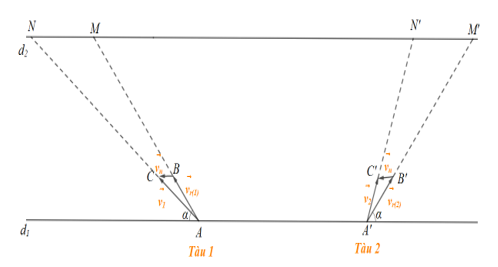
Ta biểu thị hai bờ sông là hai đường thẳng song song d₁, d₂

Giả sử tàu 1 xuất phát từ $A\in d_1$ đến M (hướng xuống hạ lưu) và bánh lái luôn được giữ để tàu tạo với bờ một góc α.

Giả sử tàu 2 xuất phát từ $A^{\text{'}}\in d_1$ đến M' (hướng lên thượng nguồn) và bánh lái luôn được giữ để tàu tạo với bờ một góc α.

Gọi $\overrightarrow{v_{r\left(1\right)}},\overrightarrow{v_{r\left(2\right)}}$ và $\overrightarrow{v_n}$ lần lượt biểu diễn vận tốc riêng của tàu 1, tàu 2 và vận tốc dòng nước.

+ Gọi B, C là các điểm sao cho $\overrightarrow{v_{r\left(1\right)}}=\overrightarrow{AB},\overrightarrow{v_n}=\overrightarrow{BC}.$

Khi đó tàu 1 chuyển động với vectơ vận tốc thực tế là $\overrightarrow{v_1}=\overrightarrow{v_{r\left(1\right)}}+\overrightarrow{v_n}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}.$

Vậy tàu 1 chuyển động theo hướng $\overrightarrow{AC}$ với đích đến là điểm N trên bờ d₂ và đi với độ lớn $\left|\overrightarrow{v_1}\right|=\left|\overrightarrow{AC}\right|=AC$.

Thời gian để tàu 1 di chuyển sang bờ d₂ là t₁ = $\frac{AN}{AC}$.

+ Gọi B', C'  là các điểm sao cho $\overrightarrow{v_{r\left(2\right)}}=\overrightarrow{A^{\text{'}}{B}^{\text{'}}},\overrightarrow{v_n}=\overrightarrow{B^{\text{'}}{C}^{\text{'}}}.$

Khi đó tàu 2 chuyển động với vectơ vận tốc thực tế là ${\overrightarrow{v}}_2=\overrightarrow{v_{r\left(2\right)}}+\overrightarrow{v_n}=\overrightarrow{A^{\text{'}}{B}^{\text{'}}}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}.$

Vậy tàu 2 chuyển động theo hướng $\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ với đích đến là điểm N'  trên bờ d₂ và đi với độ lớn $\left|\overrightarrow{v_2}\right|=\left|\overrightarrow{A^{\text{'}}{C}^{\text{'}}}\right|=A^{\text{'}}{C}^{\text{'}}$.

Thời gian để tàu 2 di chuyển sang bờ d₂ là t₂ = $\frac{A^{\text{'}}{N}^{\text{'}}}{A^{\text{'}}{C}^{\text{'}}}$.

+ Vì $\overrightarrow{v_n}=\overrightarrow{BC}=\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$ nên B, B', C, C' thẳng hàng và nằm trên đường thẳng song song với hai đường thẳng d₁ và d₂.

Khi đó theo định lý Thales, ta có: $\frac{AN}{AC}=\frac{A^{\text{'}}{N}^{\text{'}}}{A^{\text{'}}{C}^{\text{'}}}$ hay t₁ = t₂. 

Suy ra hai tàu cần thời gian như nhau để sang được đến bờ bên kia.

Vậy hai tàu sang đến bờ bên kia cùng một lúc.

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài tập cuối chương 3

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto