Trong Hình 4.27, hãy biểu thị mỗi vectơ u,v theo hai vectơ a,b, tức là tìm các số x, y, z, t

Luyện tập 3 trang 57 Toán 10 Tập 1: Trong Hình 4.27, hãy biểu thị mỗi vectơ $\overrightarrow{u},\overrightarrow{v}$ theo hai vectơ $\overrightarrow{a},\overrightarrow{b}$, tức là tìm các số x, y, z, t để $\overrightarrow{u}=x\overrightarrow{a}+y\overrightarrow{b},\overrightarrow{v}=t\overrightarrow{a}+z\overrightarrow{b}.$

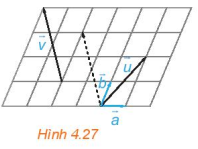
Trả lời

Giả sử các điểm O, A, B, C, M, N, P là các điểm như trong hình vẽ dưới đây.

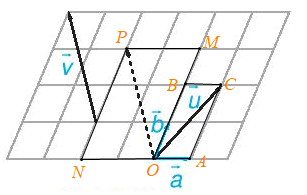
Khi đó ta có:

$$\begin{gathered} \overrightarrow{OA}=\overrightarrow{a};\overrightarrow{OB}=2\overrightarrow{b};\overrightarrow{OC}=\overrightarrow{u};\overrightarrow{OM} \\ =3\overrightarrow{b};\overrightarrow{ON}=-2\overrightarrow{a};\overrightarrow{OP}=\overrightarrow{v} \end{gathered}$$ 

Xét hình bình hành OACB, có: $\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$ (quy tắc hình bình hành)

Suy ra $\overrightarrow{u}=\overrightarrow{a}+2\overrightarrow{b}$.

Xét hình bình hành OMPN, có: $\overrightarrow{OP}=\overrightarrow{OM}+\overrightarrow{ON}$ (quy tắc hình bình hành)

Suy ra $\overrightarrow{v}=3\overrightarrow{b}+\left(-2\overrightarrow{a}\right)=-2\overrightarrow{a}+3\overrightarrow{b}.$

Vậy $\overrightarrow{u}=\overrightarrow{a}+2\overrightarrow{b},\overrightarrow{v}=-2\overrightarrow{a}+3\overrightarrow{b}.$

Xem thêm lời giải bài tập SGK Toán lớp 10 Kết nối tri thức hay, chi tiết khác:

Bài 7: Các khái niệm mở đầu

Bài 8: Tổng và hiệu của hai vectơ

Bài 9: Tích của một vecto với một số

Bài 10: Vectơ trong mặt phẳng tọa độ

Bài 11: Tích vô hướng của hai vecto

Bài tập cuối chương 4