Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích
Bài 1 trang 62 Toán 7 Tập 2:
Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.
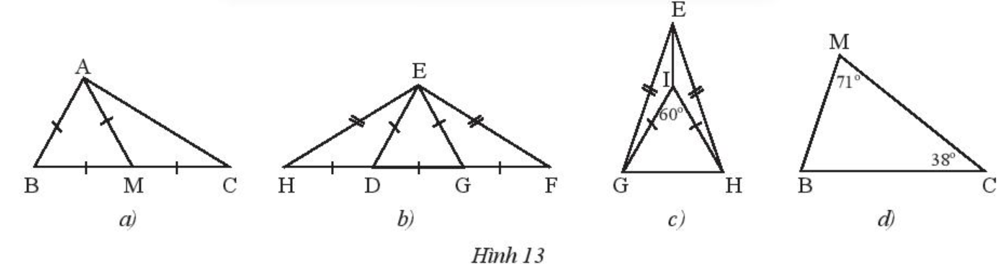
* Hình 13a):
Vì ∆AMC có AM = MC nên ∆AMC cân tại M.
Vì ∆ABM có AB = AM = BM nên ∆ABM đều.
* Hình 13b):
Vì ∆DEH có DE = DH nên ∆DEH cân tại D.
Vì ∆GEF có GE = GF nên ∆GEF cân tại G.
Vì ∆EHF có EH = EF nên ∆EHF cân tại E.
Do đó các tam giác cân: ∆DEH, ∆GEF, ∆EHF.
Vì ∆EDG có DE = EG = DG nên ∆EDG đều.
* Hình 13c):
Vì ∆EGH có EG = EH nên ∆EGH cân tại E.
Vì ∆IGH có IG = IH nên ∆IGH cân tại I.
∆IGH cân có nên ∆IGH là tam giác đều.
* Hình 13d):
Xét ∆MBC có (định lí tổng số đo ba góc của một tam giác)
Suy ra
Do đó .
Vì ∆MBC có nên ∆MBC cân tại C.
Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:
Bài 1: Góc và cạnh của một tam giác
Bài 4: Đường vuông góc và đường xiên