Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b

Bài 6 trang 63 Toán 7 Tập 2:

Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

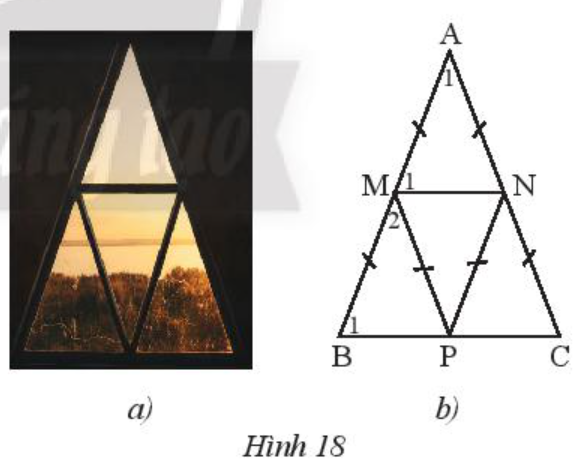
a) Cho biết ${\widehat{A}}_1=42°$. Tính số đo của ${\widehat{M}}_1,{\widehat{B}}_1,{\widehat{M}}_2$.

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Trả lời

a) ∆AMN có AM = AN nên ∆AMN cân tại A.

Suy ra ${\widehat{M}}_1=\widehat{ANM}$.

Xét ∆AMN có: ${\widehat{A}}_1+{\widehat{M}}_1+\widehat{ANM}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra ${\widehat{M}}_1+\widehat{ANM}=180°-{\widehat{A}}_1$.

Hay $2{\widehat{M}}_1=180°-{\widehat{A}}_1=180°-42°=138°$.

Do đó ${\widehat{M}}_1=69°$.

Ta có: AB = AM + MB; AC = AN + NC.

Mà AM = AN, MB = NC nên AB = AC.

Do đó ∆ABC cân tại A.

Suy ra ${\widehat{B}}_1=\widehat{C}$.

Xét ∆ABC có: ${\widehat{A}}_1+{\widehat{B}}_1+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra ${\widehat{B}}_1+\widehat{C}=180°-{\widehat{A}}_1$.

Hay $2{\widehat{B}}_1=180°-{\widehat{A}}_1=180°-42°=138°$.

Do đó ${\widehat{B}}_1=69°$.

∆MBP có MB = MP nên ∆MBP cân tại M.

Suy ra $\widehat{MBP}=\widehat{MPB}$.

Xét ∆MBP có: ${\widehat{M}}_2+{\widehat{B}}_1+\widehat{MPB}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra ${\widehat{M}}_2=180°-{\widehat{B}}_1-\widehat{MPB}$.

Hay ${\widehat{M}}_2=180°-2{\widehat{B}}_1=180°-2.69°=42°$.

Vậy ${\widehat{M}}_1=69°$; ${\widehat{B}}_1=69°$; ${\widehat{M}}_2=42°$.

b) Ta có: ${\widehat{M}}_1={\widehat{B}}_1=69°$.

Mà ${\widehat{M}}_1$ và ${\widehat{B}}_1$ ở vị trí đồng vị nên MN // BC.

Lại có: ${\widehat{M}}_2={\widehat{A}}_1=42°$.

Mà ${\widehat{M}}_2$ và ${\widehat{A}}_1$ ở vị trí đồng vị nên MP // AC.

c) • Xét ∆AMN và ∆MBP có:

AM = MB (giả thiết).

${\widehat{A}}_1={\widehat{M}}_2$ (chứng minh trên).

AN = MP (giả thiết).

Do đó ∆AMN = ∆MBP (c.g.c).

Suy ra MN = BP (hai cạnh tương ứng).

• Xét ∆MBP và ∆PMN có:

MP = PN (giả thiết).

MB = PM (giả thiết).

BP = MN (chứng minh trên).

Do đó ∆MBP = ∆PMN (c.c.c).

• Do MP // AC nên $\widehat{MPN}=\widehat{PNC}$ (hai góc so le trong).

Xét ∆PMN và ∆NPC có:

PM = NP (giả thiết).

$\widehat{MPN}=\widehat{PNC}$ (chứng minh trên).

PN = NC (giả thiết).

Do đó ∆PMN = ∆NPC (c.g.c).

Vậy bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc và cạnh của một tam giác

Bài 2: Tam giác bằng nhau

Bài 3: Tam giác cân

Bài 4: Đường vuông góc và đường xiên

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác