Cho tam giác ABC cân tại A có  (Hình 15).a) Tính góc B, góc C

Bài 3 trang 63 Toán 7 Tập 2:

Cho tam giác ABC cân tại A có $\widehat{A}=56°$ (Hình 15).

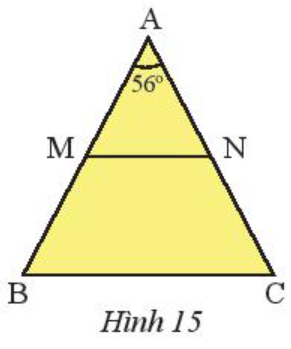
a) Tính $\widehat{B},\widehat{C}$.

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.

c) Chứng minh rằng MN // BC.

Trả lời

a) Theo đề bài: ∆ABC cân tại A nên $\widehat{B}=\widehat{C}$.

Xét ∆ABC có: $\widehat{A}+\widehat{B}+\widehat{C}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{B}+\widehat{C}=180°-\widehat{A}$.

Do đó $2\widehat{B}=180°-56°=124°$ (vì $\widehat{B}=\widehat{C}$) nên $\widehat{B}=\frac{124°}{2}=62°$

Vậy $\widehat{B}=\widehat{C}=62°$.

b) Vì M là trung điểm của AB nên:

AM = $\frac{1}{2}$AB hay AB = 2AM.

Vì N là trung điểm của AC nên:

AN = $\frac{1}{2}$AC hay AC = 2AN.

Mà ∆ABC cân tại A nên AB = AC hay 2AM = 2AN.

Do đó AM = AN.

Tam giác AMN có AM = AN nên tam giác AMN cân tại A.

Vậy tam giác AMN cân tại A.

c) Vì ∆AMN cân tại A nên $\widehat{AMN}=\widehat{ANM}$.

Xét ∆AMN có $\widehat{A}+\widehat{AMN}+\widehat{ANM}=180°$ (định lí tổng số đo ba góc của một tam giác)

Suy ra $\widehat{AMN}+\widehat{ANM}=180°-\widehat{A}$.

Hay $2\widehat{AMN}=180°-56°=124°$.

Do đó $\widehat{AMN}=\widehat{ANM}=62°$.

Khi đó $\widehat{ABC}=\widehat{AMN}=62°$.

Mà hai góc này ở vị trí đồng vị nên MN // BC.

Vậy MN // BC.

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

Bài 1: Góc và cạnh của một tam giác

Bài 2: Tam giác bằng nhau

Bài 3: Tam giác cân

Bài 4: Đường vuông góc và đường xiên

Bài 5: Đường trung trực của một đoạn thẳng

Bài 6: Tính chất ba đường trung trực của tam giác