10 câu hỏi trắc nghiệm thuộc Dạng 4: Chứng minh hai vectơ hay hai đường thẳng vuông góc có đáp án

Câu 1:

Cho tam giác ABC có $\vec{B A} . \vec{B C} = \vec{0}$ . Khẳng định nào sau đây là đúng ?

A. Tam giác ABC vuông tại A;

B. Tam giác ABC vuông tại B;

C. Tam giác ABC vuông tại C;

D. Tam giác ABC là tam giác cân.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: B.

Ta có:

$\vec{B A} . \vec{B C} = \vec{0} \Leftrightarrow \vec{B A} ⊥ \vec{B C} \Leftrightarrow B A ⊥ B C$

Do đó, tam giác ABC vuông tại B.

Câu 2:

Cho hình vuông ABCD. Khẳng định nào sau đây là đúng ?

A. $\vec{A B} . \vec{A C} = 0$

B. $\vec{A B} . \vec{C D} = 0$

C. $\vec{A B} . \vec{A D} = 0$

D. $\vec{A B} . \vec{B D} = 0$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

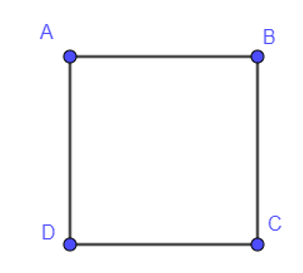
Cho hình vuông ABCD. Khẳng định nào sau đây là đúng ? (ảnh 1)

Ta có: Do ABCD là hình vuông nên $A B ⊥ A D \Leftrightarrow \vec{A B} ⊥ \vec{A D} \Leftrightarrow \vec{A B} . \vec{A D} = 0$ .

Câu 3:

Cho hình thoi ABCD tâm O. Khẳng định nào sau đây là sai ?

A. $\vec{A B} . \vec{A C} = 0$

B. $\vec{A C} . \vec{B D} = 0$

C. $\vec{A O} . \vec{D O} = 0$

D. $\vec{O B} . \vec{O C} = 0$

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

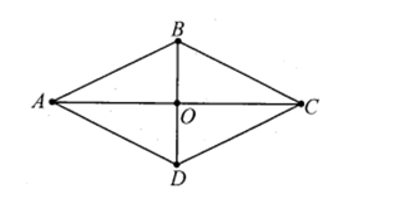
Cho hình thoi ABCD tâm O. Khẳng định nào sau đây là sai ? (ảnh 1)

Do ABCD là hình thoi nên AB không vuông góc với AC nên $\vec{A B} . \vec{A C} \neq 0$ .

Hai đường chéo AC và BD của hình thoi vuông góc với nhau tại O nên

$\vec{A C} . \vec{B D} = 0$ ; $\vec{A O} . \vec{D O} = 0$ ; $\vec{O B} . \vec{O C} = 0$ .

Câu 4:

Cho đường tròn (O; R) có hai dây cung AA’, BB’ vuông góc với nhau tại S, gọi M là trung điểm của AB. Hai đường thẳng nào sau đây vuông góc với nhau ?

A. SM và AB;

B. SM và SA;

C. SM và A’B’;

D. SM và AB’.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Ta có:

$\vec{S M} . \vec{A' B'} = \frac{1}{2} (\vec{S A} + \vec{S B}) (\vec{S B'} - \vec{S A'})$ (áp dụng quy tắc trung điểm và quy tắc trừ)

$= \frac{1}{2} (\vec{S A} . \vec{S B'} - \vec{S A} . \vec{S A}' + \vec{S B} . \vec{S B'} - \vec{S B} . \vec{S A}')$

Lại có: AA’ vuông góc với BB’ tại S nên ta có:

$\vec{S A} . \vec{S B'} = 0$

$\vec{SB} . \vec{SA'} = 0$

$\vec{S A} . \vec{S A'} = \vec{S B} . \vec{S B'}$

Từ đó suy ta $\vec{S M} . \vec{A' B'} = 0$

Vậy SM vuông góc với A’B’.

Câu 5:

Cho hình thang ABCD với hai đáy là AB, CD có: $(\vec{A B} - \vec{A D}) . \vec{A C} = 0$ . Khẳng định nào sau đây là đúng ?

A. BD vuông góc với AC;

B. AB vuông góc với AC;

C. AB vuông góc với DC;

D. BD vuông góc với DC.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

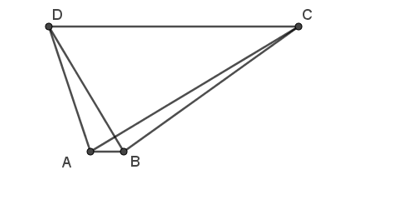
Cho hình thang ABCD với hai đáy là AB, CD có: (vecto AB-AD). vecto AC=0 (ảnh 1)

Ta có:

$(\vec{A B} - \vec{A D}) . \vec{A C} = 0 \Leftrightarrow \vec{D B} . \vec{A C} = \vec{0} \Leftrightarrow \vec{D B} ⊥ \vec{A C}$

Vậy BD vuông góc với AC.

Câu 6:

Cho hai vectơ $\vec{a}$ và $\vec{b}$ vuông góc, $|\vec{a}| = 1, |\vec{b}| = \sqrt{2}$ . Các vectơ nào sau đây vuông góc ?

A. $2 \vec{a} - \vec{b}$ và $\vec{a} + \vec{b}$ ;

B.

2 \vec{a} - \vec{b}

và

\vec{a} + \vec{b}

;

C.

2 \vec{a} + \vec{b}

và

\vec{a} - \vec{b}

;

D.

\vec{a} - \vec{b}

và

\vec{a} + \vec{b}

.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: A.

Do vectơ $\vec{a}$ và $\vec{b}$ vuông góc nên ta có: $\vec{a} . \vec{b} = 0$ .

Ta có:

$(2 \vec{a} - \vec{b}) (\vec{a} + \vec{b}) = 2 {\vec{a}}^{2} + 2 \vec{a} . \vec{b} - \vec{a} . \vec{b} - {\vec{b}}^{2}$

$= 2 {|\vec{a}|}^{2} + 2 \vec{a} . \vec{b} - \vec{a} . \vec{b} - {|\vec{b}|}^{2}$

$= {2.1}^{2} + 2.0 - 0 - {(\sqrt{2})}^{2} = 0$

Vậy $2 \vec{a} - \vec{b}$ và $\vec{a} + \vec{b}$ vuông góc.

Tương tự, ta kiểm tra tích vô hướng của các cặp vectơ ở các đáp án B, C, D, các tích này đều khác 0 nên chúng không vuông góc.

Câu 7:

Cho hai vectơ $\vec{i}$ và $\vec{j}$ vuông góc với nhau, biết $|\vec{i}| = |\vec{j}| = 1$ , cho $\vec{a} = 9 \vec{i} + 3 \vec{j}$ và $\vec{v} = \vec{i} - 3 \vec{j}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{a}

và

\vec{v}

ngược hướng;

B.

\vec{a}

và

\vec{v}

cùng hướng;

C.

\vec{a}

và

\vec{v}

bằng nhau;

D.

\vec{a}

và

\vec{v}

vuông góc.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Do vectơ $\vec{i}$ và $\vec{j}$ vuông góc nên ta có: $\vec{i} . \vec{j} = 0$

Ta có:

$\vec{a} . \vec{v} = (9 \vec{i} + 3 \vec{j}) (\vec{i} - 3 \vec{j}) = 9 {\vec{i}}^{2} - 27 \vec{i} . \vec{j} + 3 \vec{i} . \vec{j} - 9 {\vec{j}}^{2}$

$= 9 {|\vec{i}|}^{2} - 27 \vec{i} . \vec{j} + 3 \vec{i} . \vec{j} - 9 {|\vec{j}|}^{2}$

$= 9.1 - 27.0 + 3.0 - 9.1 = 0$

Vậy $\vec{a}$ và $\vec{v}$ vuông góc.

Câu 8:

Cho hai vectơ $\vec{i}$ và $\vec{j}$ vuông góc với nhau, biết $|\vec{i}| = |\vec{j}| = 1$ , cho $\vec{a} = 3 \vec{i} + 4 \vec{j}$ và $\vec{v} = \vec{i} - 2 \vec{j}$ . Khẳng định nào sau đây là đúng ?

A. $\vec{a}$ và $\vec{v}$ ngược hướng;

A.

\vec{a}

và

\vec{v}

ngược hướng;

C. $\vec{a}$ và $\vec{v}$ không vuông góc;

D. $\vec{a}$ và $\vec{v}$ vuông góc.

A.

\vec{a}

và

\vec{v}

ngược hướng;

B. $\vec{a}$ và $\vec{v}$ cùng hướng

C.

\vec{a}

và $\vec{v}$ không vuông góc;

D.

\vec{a}

và

\vec{v}

vuông góc.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Do vectơ $\vec{i}$ và $\vec{j}$ vuông góc nên ta có: $\vec{i} . \vec{j} = 0$ .

Ta có:

$\vec{a} . \vec{v} = (3 \vec{i} + 4 \vec{j}) (\vec{i} - 2 \vec{j}) = 3 {\vec{i}}^{2} - 6 \vec{i} . \vec{j} + 4 \vec{i} . \vec{j} - 8 {\vec{j}}^{2}$

$= 3 {|\vec{i}|}^{2} - 6 \vec{i} . \vec{j} + 4 \vec{i} . \vec{j} - 8 {|\vec{j}|}^{2}$

$= 3.1 - 6.0 + 4.0 - 8.1 = - 5 \neq 0$

Vậy $\vec{a}$ và $\vec{v}$ không vuông góc.

Câu 9:

Cho hai vectơ $\vec{i}$ và $\vec{j}$ vuông góc với nhau, biết $|\vec{i}| = |\vec{j}| = 1$ , cho $\vec{u} = 10 \vec{i} - 5 \vec{j}$ và $\vec{w} = - \vec{i} - 2 \vec{j}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{u}

và

\vec{w}

ngược hướng;

B.

\vec{u}

và

\vec{w}

cùng hướng;

C.

\vec{u}

và

\vec{w}

không vuông góc;

D.

\vec{u}

và

\vec{w}

vuông góc.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: D.

Do vectơ $\vec{i}$ và $\vec{j}$ vuông góc nên ta có: $\vec{i} . \vec{j} = 0$ .

Ta có:

$\vec{u} . \vec{w} = (10 \vec{i} - 5 \vec{j}) (- \vec{i} - 2 \vec{j}) = - 10 {\vec{i}}^{2} - 20 \vec{i} . \vec{j} + 5 \vec{i} . \vec{j} + 10 {\vec{j}}^{2}$

$= - 10 {|\vec{i}|}^{2} - 20 \vec{i} . \vec{j} + 5 \vec{i} . \vec{j} + 10 {|\vec{j}|}^{2}$

$= - 10.1 - 20.0 + 5.0 + 10.1 = 0$

Vậy $\vec{a}$ và $\vec{v}$ vuông góc.

Câu 10:

Cho hai vectơ $\vec{i}$ và $\vec{j}$ vuông góc với nhau, biết $|\vec{i}| = |\vec{j}| = 1$ , cho $\vec{u} = \vec{i} - 5 \vec{j}$ và $\vec{w} = - \vec{i} - 2 \vec{j}$ . Khẳng định nào sau đây là đúng ?

A.

\vec{u}

và

\vec{w}

ngược hướng;

B.

\vec{u}

và

\vec{w}

cùng hướng;

C.

\vec{u}

và

\vec{w}

không vuông góc;

D.

\vec{u}

và

\vec{w}

vuông góc.

Xem đáp án

Hướng dẫn giải:

Đáp án đúng là: C.

Do vectơ $\vec{i}$ và $\vec{j}$ vuông góc nên ta có: $\vec{i} . \vec{j} = 0$ .

Ta có:

$\vec{u} . \vec{w} = (\vec{i} - 5 \vec{j}) (- \vec{i} - 2 \vec{j}) = - {\vec{i}}^{2} - 2 \vec{i} . \vec{j} + 5 \vec{i} . \vec{j} + 10 {\vec{j}}^{2}$

$= - {|\vec{i}|}^{2} - 2 \vec{i} . \vec{j} + 5 \vec{i} . \vec{j} + 10 {|\vec{j}|}^{2}$

$= - 1 - 2.0 + 5.0 + 10.1 = 9 \neq 0$

Vậy $\vec{u}$ và $\vec{w}$ không vuông góc.

Trắc nghiệm Toán 10 CTST Bài 4. Tích vô hướng của hai vectơ có đáp án

Dạng 4: Chứng minh hai vectơ hay hai đường thẳng vuông góc có đáp án

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương